Nejako sa stalo, že mám naozaj rád najrôznejšie algoritmy, ktoré majú jasné a logické matematické opodstatnenie) Ale často je ich popis na internete taký preťažený vzorcami a výpočtami, že všeobecný význam Algoritmus je jednoducho nemožné pochopiť. Pochopenie podstaty a princípu fungovania zariadenia / mechanizmu / algoritmu je však oveľa dôležitejšie ako zapamätanie si obrovských vzorcov. Nech je to akokoľvek banálne, zapamätať si ani stovky vzorcov ničomu nepomôže, ak nevieš ako a kde ich aplikovať 😉 Vlastne načo to všetko je.. rozhodol som sa pomotať popis niektorých algoritmov, s ktorými som sa musel popasovať s v praxi. Pokúsim sa nepreťažovať matematickými výpočtami, aby bol materiál jasný a čítanie bolo ľahké.

A dnes o tom budeme hovoriť Kalmanov filter, poďme zistiť, čo to je, prečo a ako sa používa.

Začnime malým príkladom. Postavme sa pred úlohu určiť súradnicu letiaceho lietadla. Okrem toho by samozrejme mala byť súradnica (označme ju) určená čo najpresnejšie.

V lietadle sme predinštalovali senzor, ktorý nám poskytuje požadované údaje o polohe, ale ako všetko v tomto svete, ani náš senzor nie je dokonalý. Preto namiesto hodnoty dostaneme:

kde je chyba snímača, teda náhodná veličina. Z nepresných údajov meracieho zariadenia teda musíme získať súradnicovú hodnotu () čo najbližšie k skutočnej polohe lietadla.

Problém je nastolený, prejdime k jeho riešeniu.

Dajte nám vedieť riadiacu akciu (), vďaka ktorej lietadlo letí (pilot nám povedal, ktoré páky ťahá 😉). Potom, keď poznáme súradnicu v k-tom kroku, môžeme získať hodnotu v kroku (k + 1):

Zdá sa, že to je to, čo potrebujete! A tu nie je potrebný žiadny Kalmanov filter. Ale nie všetko je také jednoduché.. V skutočnosti nemôžeme brať do úvahy všetko vonkajšie faktory ovplyvňujúci let, takže vzorec má nasledujúcu formu:

kde je chyba spôsobená vonkajšími vplyvmi, nedokonalosťou motora a pod.

tak čo sa stane? V kroku (k + 1) máme po prvé nepresný údaj snímača a po druhé nepresne vypočítanú hodnotu získanú z hodnoty v predchádzajúcom kroku.

Myšlienkou Kalmanovho filtra je získať presný odhad požadovanej súradnice (pre náš prípad) z dvoch nepresných hodnôt (pričom ich berieme s rôznymi váhovými koeficientmi). V všeobecný prípad, nameraná hodnota môže byť absolútne ľubovoľná (teplota, rýchlosť..). Čo sa stane:

Autor: matematické výpočty môžeme získať vzorec na výpočet Kalmanovho koeficientu v každom kroku, ale ako bolo dohodnuté na začiatku článku, nebudeme sa ponoriť do výpočtov, najmä preto, že v praxi sa zistilo, že Kalmanov koeficient má vždy tendenciu určitú hodnotu... Dostávame prvé zjednodušenie nášho vzorca:

Teraz predpokladajme, že neexistuje žiadna komunikácia s pilotom a nepoznáme činnosť riadenia. Zdalo by sa, že v tomto prípade nemôžeme použiť Kalmanov filter, ale nie je to tak 😉 To, čo nepoznáme, jednoducho „vyhodíme“ zo vzorca

Získame najjednoduchší Kalmanov vzorec, ktorý sa napriek takýmto „tvrdým“ zjednodušeniam dokonale vyrovná so svojou úlohou. Ak výsledky znázorníte graficky, dostanete niečo ako nasledovné:

Ak je náš senzor veľmi presný, potom by sa váhový faktor K prirodzene mal blížiť k jednej. Ak je situácia opačná, to znamená, že náš snímač nie je veľmi dobrý, potom by K malo byť bližšie k nule.

To je pravdepodobne všetko, práve tak sme prišli na Kalmanov algoritmus filtrovania! Dúfam, že článok bol užitočný a zrozumiteľný =)

Tieto filtre sa v literatúre nazývajú aj Kalman-Bucyho filtre. Oproti Wienerovmu problému je tu použitý tvarovací filter (obr. 4.2), ktorý je určitým dynamický systém popísané lineárne diferenciálne rovnice vo všeobecnom prípade s premenlivými koeficientmi a excitovaný multivariačným bielym šumom a s Gaussovým rozdelením.

Ryža. 4.2. Optimálny Kalmanov filter.

Na obr. 4.2 je to znázornené pre spojitý prípad.

Modelový je tvarovací filter poháňaný bielym šumom vstupný proces riadiace systémy (analógový systém). Stav tohto modelu v každom časovom okamihu určuje súprava stavové premenné ktorých počet je určený typom vstupného signálu, t.j. jeho korelačnou funkciou alebo spektrálnou hustotou. Zisťovanie stavu analógového systému sa vykonáva meracím zariadením, ktoré na svojom výstupe dáva súbor vstupných signálov riadiaceho systému, tj viacrozmerný vstupný signál skreslený aditívnym šumom, ktorým je viacrozmerný biely šum s Gaussovkou. distribúcia. V diskrétnej verzii problému R. Kalmana sa vstupné a výstupné hodnoty tvarovacieho filtra zvažujú v diskrétnych časových okamihoch, kde je celé číslo, perióda diskrétnosti. V tomto prípade

model vstupného signálu je opísaný sústavou lineárnych diferenčných rovníc.

Je potrebné skonštruovať dynamický systém – Kalmanov filter, ktorý dáva najlepšia známka viacrozmerná veličina vo forme súboru výstupných hodnôt filtra, z ktorého sa ďalej dajú lineárne vytvárať výstupné hodnoty riadiacich systémov.

Odhad musí byť nezaujatý, t.j. jeho matematické očakávanie

Výraz (4.9) sa tiež píše v inej forme. Pre dané merania veličiny od okamihu do okamihu I musí mať odhad v určitom časovom okamihu vlastnosť

Okrem toho je uložená podmienka minimálneho rozptylu chyby odhadu, ktorá sa zapíše do formulára

kde Γ je ľubovoľná pozitívne definitívna matica. Maticový súčin je kvadratická forma s váhovou maticou G. Výraz (4.11) znamená, že odhad veličiny spĺňa podmienku minimálneho rozptylu chyby každej zo zložiek množiny veličín.

Pri použití Kalmanových filtrov sú možné nasledujúce prípady.

1. Pre kontinuálne systémy je vyriešený problém optimálnej filtrácie, to znamená problém oddelenia užitočného signálu od aditívnej zmesi užitočného signálu a šumu. V tomto prípade Kalmanov filter poskytuje odhad množiny premenných počínajúc od určitého bodu v čase vo forme počiatočnej hrubej aproximácie, ktorá je tým presnejšia, čím je apriórna informácia o množine viac. času sa tento odhad zlepšuje a neustále sa približuje k teoreticky dosiahnuteľnému

hodnotu, ktorá už nezávisí od apriórnej informácie o hodnote a, určujú vlastnosti tvarovacieho filtra a rušenie meracieho zariadenia.

V ustálenom stave sa Kalmanov filter zhoduje s Wienerovým filtrom a dáva rovnakú odhadovanú hodnotu.

2. V diskrétnych systémoch je možné formulovať problém optimálneho určenia odhadu pre čas z údajov meraní vstupného signálu v časových bodoch od do, teda problém optimálnej predikcie jedného (alebo viacerých) hodín. cykly dopredu. Táto úloha má zmysel aj v prípade nulového rušenia meracieho zariadenia.

3. V diskrétnych systémoch je možné formulovať aj problém optimálneho filtrovania, teda problém stanovenia odhadu z údajov predchádzajúcich meraní vrátane časového okamihu.Tento problém je možné riešiť v prípade, že konfliktná situácia spôsobená hlukom merania.

Aplikované na digitálne systémy automatické ovládanie a regulácii treba poznamenať nasledovné. V digitálnom riadiacom systéme spravidla meranie vstupného signálu v určitom okamihu neumožňuje korigovať jeho výstupnú hodnotu v rovnakom čase, pretože reakcia spojitej časti systému (jeho funkcia zníženej hmotnosti) k vstupnému signálu v rovnakom časovom okamihu sa rovná nule a nemôže sa rovnať nule. Preto výstupnú hodnotu systému v určitom časovom bode možno určiť len ako výsledok predikcie z výsledkov predchádzajúcich meraní.

Vyššie uvedený druhý problém vyriešený Kalmanovými filtrami je zrejmý praktický význam pre digitálne automatické systémy. Treba však poznamenať, že v mnohých prípadoch je potrebné zvoliť dobu diskrétnosti digitálneho riadiaceho systému z rôznych dôvodov (stabilita, možnosť straty vstupné informácie a ďalšie) je relatívne malý (tisíciny a stotiny sekundy). Tá istá súvislá časť riadiaceho systému môže obsahovať extrapolátory, ktoré dobre predpovedajú požadovaný výstupný proces. Takéto extrapolátory môžu byť integrátory rôzneho druhu a samotné riadiace objekty. Preto problém optimálneho predpovedania pre

takt vpred v niektorých prípadoch stráca zmysel a môže viesť k nesprávne rozhodnutia konkrétny technický problém. Predpovedanie niekoľkých hodinových cyklov však zvyčajne nestráca svoj význam ani pri malých intervaloch diskrétnosti. Ale v tomto prípade sa to prakticky zhoduje s prípadom predpovedania v spojitých systémoch.

Tretí problém, riešený Kalmanovým filtrom, má veľké možnosti, keďže zahŕňa hľadanie optimálne riešenieúlohy konštrukcie riadiaceho systému so súčasným pôsobením užitočného signálu a rušenia. Obmedzenia používania Kalmanových filtrov na vykresľovanie digitálnych systémov riadenie sú určené nasledujúcimi okolnosťami.

1. Konštrukcia Kalmanovho filtra predpokladá úplnú apriórnu informáciu o štruktúre tvarovacieho filtra, tj úplnú apriórnu informáciu o štatistických vlastnostiach vstupného signálu a úplnú informáciu o pôsobiacom šume. Ak tieto informácie nie sú veľmi spoľahlivé, potom tu stráca optimalizácia zmysel, alebo treba ísť cestou výraznej komplikácie systému pomocou adaptačných princípov.

2. Použitie Kalmanových filtrov predpokladá, že neexistujú žiadne obmedzenia na štruktúru optimálneho systému. Preto prechod z požadovanej teoretickej štruktúry na reálnu štruktúru riadiaceho systému, obsahujúcu určité špecifikované prvky, môže výrazne zhoršiť výsledky. Tieto obmedzenia sa zvyčajne netýkajú tých prípadov, keď je celý systém na generovanie odhadu viacrozmernej veličiny vybudovaný napríklad na digitálnom počítači a neobsahuje vopred určené prvky riadiaceho systému.

3. Pri konštrukcii Kalmanovho filtra sa predpokladá, ako bude ukázané nižšie, že na spracovanie možno použiť predchádzajúce hodnoty vstupných signálov, kde je poradie diferenčnej rovnice popisujúcej tvarovací filter (obr. 4.2 ). V reálnych podmienkach prevádzky číslicového riadiaceho systému je možné využiť na spracovanie väčší počet predchádzajúcich vstupných signálov, čím je možné výrazne znížiť vplyv šumu pri meraní vstupných signálov a získať výsledky, ktoré sú lepšie ako Kalmanov filter.

Použitie skutočných filtrov. V niektorých prípadoch riadiacich systémov budov je vstupný signál nastavený sám

charakteristiky, ale nedochádza k interferenciám alebo sú relatívne malé, v dôsledku čoho konštrukcia optimálneho systému v zmysle Wienera alebo Kalmana stráca zmysel. To však neznamená, že skutočný riadiaci systém je možné skonštruovať s ľubovoľne malým rozptylom chýb. V idealizovanom prípade Wienerovho alebo Kalmanovho filtra nie sú na navrhnutý systém kladené žiadne predbežné obmedzenia. Zvýšenie celkového koeficientu za účelom zlepšenia vernosti užitočného signálu je tu obmedzené zvýšením chyby v dôsledku zvýšenia prenosu rušenia pôsobiaceho na vstupe. Vzniká tak konfliktná situácia.

V reálnych systémoch nemusí dochádzať k rušeniu vstupného signálu, ale zvýšenie celkového zisku je v tomto prípade obmedzené priblížením sa k hranici oscilačnej stability, čo spôsobuje zvýšenie chyby v dôsledku zvýšenia oscilácie systém. Maximálne dosiahnuteľné ziskové faktory v tomto prípade budú určené prítomnosťou určitého súboru väzieb s malými časovými konštantami v reálnom systéme, ktorých vplyv už nie je možné kompenzovať.

V tomto zmysle je prítomnosť množiny väzieb charakterizovaných súčtom ich časových konštánt alebo výsledným časovým oneskorením v konečnom výsledku ekvivalentná pôsobeniu na vstupe nejakého šumu. V oboch prípadoch sa ukazuje, že maximálna presnosť systému je obmedzená a odchýlka chyby nemôže byť menšia ako určitá hraničná hodnota.

Odhad minimálneho súčtu časových konštánt alebo celkového časového posunu v navrhovanom systéme dokáže urobiť dostatočne skúsený projektant pri výbere jeho prvkov. V tomto prípade samozrejme môže projektant túto sumu ovplyvniť v smere jej znižovania. Môže za to však prechod na pokročilejšie a drahšie prvky. Preto je možné túto sumu vždy odhadnúť pre danú konkrétnu situáciu a závisí od stupňa rozvoja použitej technológie.

Zohľadnenie vplyvu malých časových konštánt kladie na navrhovaný systém určité obmedzenia, ktoré pri riešení problému optimálnej syntézy zvyčajne chýbajú. V zásade možno tieto obmedzenia zohľadniť vo formulári

nejaký ekvivalentný hluk. Vysvetlíme si to na jednoduchom príklade. Nech má užitočný signál na vstupe spektrálnu hustotu pre deriváciu vo forme

kde je rozptyl prvej derivácie, a je nejaká časová konštanta a spektrálna hustota šumu na vstupe zodpovedá biely šum... Nech je optimálna hodnota celkového zisku systému, ktorý má prenosovú funkciu v otvorenom stave formulára

S absenciou krížová korelácia odchýlka chyby medzi užitočným signálom a interferenciou

Diferenciácia (4.14) vzhľadom na zisk a prirovnanie derivácie k nule dáva podmienku pre minimálny rozptyl chyby

Nahradením (4.15) za (4.14) vznikne minimálna hodnota odchýlka chyby zodpovedajúca optimálnej hodnote celkového zisku:

Nech je problém teraz vyriešený optimálna voľba zisk pre rovnaký užitočný vstupný signál a bez rušenia, ale pod podmienkou, že prenosová funkcia systému s otvorenou slučkou môže mať tvar

kde je celkové časové oneskorenie, ktoré nie je možné odstrániť v riadiacom systéme pre vybrané

prvkov. Takéto celkové časové oneskorenie môže byť zavedené napríklad v prítomnosti niekoľkých aperiodických spojení s malými časovými konštantami. Rozptyl chyby v tomto prípade

Integrál (4.18) sa neberie elementárne. Jeho približný výpočet dáva

Minimálny rozptyl chyby bude vtedy, keď podmienka

Substitúcia tejto hodnoty zosilnenia v (4.19) dáva minimálny rozptyl chyby

Rovnanie (4.16) a (4.21) vám umožňuje určiť úroveň ekvivalentného bieleho šumu

čo pri svojom pôsobení vedie k rovnakému efektu ako vplyv neodstrániteľného časového oneskorenia.

Samozrejme sú možné aj zložitejšie situácie, keď okrem prítomnosti niektorých malých parametrov v systéme pôsobia na vstupe systému aj skutočné zvuky. A v tomto prípade je v zásade možné nájsť ekvivalentné rušenie, berúc do úvahy prítomnosť týchto dvoch faktorov. Táto cesta však vedie k značnej komplikácii výpočtov. Preto ekvivalencia malých časových konštánt v ich konečnom pôsobení so vstupným šumom v riadiacom systéme má len určitý kognitívny význam. Samotný problém syntézy riadiaceho systému v tomto prípade možno jednoduchšie vyriešiť na základe v súčasnosti vyvinutých inžinierskych metód, ktoré zahŕňajú

použitie typických prenosových funkcií, typické prechodové charakteristiky, typické logaritmické frekvenčné charakteristiky atď.

Pri konštrukcii skutočných filtrov, ktoré sú automatickými riadiacimi systémami, ktoré fungujú tak v prítomnosti šumu na vstupe, ako aj v jeho neprítomnosti, by teda ich štruktúra mala zodpovedať štruktúre znázornenej na obr. 4.3. Na vstup systému sa privádza aditívna zmes užitočného signálu a šumu alebo len užitočný signál. Užitočný signál môže byť pravidelná funkcia času, stacionárny náhodný proces alebo nestacionárny proces. Interferencia sa spravidla prezentuje ako náhodný stacionárny proces s nulovou strednou hodnotou. Okrem toho môže byť systém ovplyvnený Eperturbáciou alebo niekoľkými poruchami aplikovanými na rôzne body objektu.

Ryža. 4.3. Skutočný jednorozmerný filter.

Lineárny operátor sa tvorí z procesu a referenčnej akcie, ktorá musí byť reprodukovaná na výstupe riadiaceho systému s prenosovou funkciou. Riadiaci systém musí pozostávať z nemeniteľnej časti, za ktorú možno považovať napr. spoje s malými časovými konštantami alebo spojkou s časovým oneskorením a premennou časťou, vo vzťahu ku ktorej existuje sloboda výberu z hľadiska jej prenosovej funkcie.

Tu sa teda musíme zaoberať polotuhou štruktúrou riadiaceho systému. Všimnite si, že vyššie formulovaný koncept nemennej časti systému je trochu odlišný od toho, ktorý sa zvyčajne používa v literatúre, keď sa nemenná časť jednoducho chápe ako riadiaci objekt s jej prenosovou funkciou. Faktom je, že použitie rôznych korekčných prostriedkov (sekvenčný typ, paralelný typ, spätné väzby) vám umožňuje aktívne ovplyvňovať prenosovú funkciu objektu a podľa potreby ho meniť. To sa však dá len urobiť

do určitej hranice, ktorá je charakterizovaná minimálnymi hodnotami „zostatkových“ časových konštánt alebo časových oneskorení, ktoré má projektant k dispozícii. Preto je tu nemenná časť systému definovaná v tomto zmysle.

Pri konštrukcii skutočných filtrov sú možné nasledujúce prípady.

1. V závislosti od špecifikácie charakteristík užitočného signálu, rušenia, rušenia a nemennej časti systému je potrebné nájsť prenosovú funkciu riadiaceho systému, ktorá zabezpečí splnenie požiadaviek na presnosť určenú koreňovým systémom. - stredná kvadratická chyba, maximálna chyba, najpravdepodobnejšia chyba alebo iné a ďalšie požiadavky na systém formulované v § 4.1.

Úloha môže byť uľahčená, ak na vstupe nie sú žiadne zvuky alebo ak na riadiaci objekt nie sú aplikované žiadne rušenia, alebo oboje chýba. Nestáva sa však triviálnym.

2. Pod podmienkou určenia charakteristík užitočného signálu, šumu, rušenia a nemennej časti systému je potrebné určiť prenosovú funkciu riadiaceho systému, pri ktorej je splnená podmienka minimalizácie odchýlky chyby, čo zodpovedá konštrukcii optimálneho systému.

Treba si uvedomiť, že konštrukcia skutočných filtrov je oveľa náročnejšia úloha ako konštrukcia napríklad Wienerovho filtra. Dá sa to overiť porovnaním obr. 4.1 a obr. 4.3. Navyše, implementácia prvého vyššie formulovaného problému je často náročnejšia ako konštrukcia optimálneho systému. Ide o to, že vždy je možné zostaviť optimálny systém pre dostupné počiatočné údaje a ťažkosti s nájdením optimálnej prenosovej funkcie sú čisto matematické. Používanie počítačov v súčasnosti tieto ťažkosti do značnej miery odstraňuje. Preto sa problém optimalizácie riadiaceho systému, napríklad minimalizovaním rozptylu chyby, v niektorých prípadoch stáva teraz triviálnym.

Zároveň problém skonštruovať systém s požadovanou presnosťou s dostupnými počiatočnými údajmi nemusí

mať riešenia. Ak je napriek tomu potrebné vyriešiť tento problém, je možné, že bude potrebné vyriešiť celý komplex. najťažšie problémy spojené s prechodom na pokročilejšie prvky riadiaceho systému, získanie Ďalšie informácie na vstupných signáloch systému, napríklad podľa prvej, druhej a vyššej derivácie referenčnej akcie, prechod na pokročilejšie prostriedky spracovania informácií a pod.

Preto prvý problém formulovaný vyššie nestráca na aktuálnosti, napriek rozvoju teórie optimálnych systémov, a navyše má v súčasnosti najaktívnejší vplyv na vývoj technológie automatického riadenia.

Ryža. 4.4. Skutočný viacrozmerný filter.

Keď idete na viacrozmerné systémy kontrolná úloha konštrukcie skutočných filtrov si zachováva svoj význam. Štrukturálna schéma pre tento prípad je znázornené na obr. 4.4. Diagram zobrazuje maticové stĺpce užitočných vstupných akcií a šumov nastavovacích akcií rušivých akcií regulovaných veličín a chýb, ako aj maticu prenosových funkcií.

Všetky vyššie uvedené úvahy pre konštrukciu spojitých riadiacich systémov založených na použití reálnych filtrov si prakticky zachovávajú svoj význam pre digitálne riadiace systémy s prihliadnutím na ich zvláštnosti - kvantovanie času a kvantovanie úrovne.

Tento filter sa používa v rôznych oblastiach – od rádiotechniky až po ekonomiku. Tu rozoberieme hlavnú myšlienku, význam, podstatu tohto filtra. Bude to prezentované najjednoduchším možným spôsobom.
Predpokladajme, že potrebujeme zmerať nejaké množstvá objektu. V rádiotechnike sa najčastejšie zaoberajú meraniami napätí na výstupe určitého zariadenia (senzor, anténa atď.). V príklade s elektrokardiografom (pozri) sa zaoberáme meraniami biopotenciálov na ľudskom tele. Napríklad v ekonomike môžu byť meranou hodnotou výmenné kurzy. Kurz na každý deň rôzne meny, t.j. každý deň nám „jeho miery“ dávajú inú hodnotu. A ak to zovšeobecňovať, tak to môžeme povedať väčšinaľudská činnosť (ak nie všetka) sa redukuje práve na neustále merania-porovnávanie určitých veličín (viď kniha).
Predpokladajme teda, že neustále niečo meriame. Predpokladajme tiež, že naše merania vždy prichádzajú s nejakou chybou - je to pochopiteľné, pretože neexistujú ideálne meracie prístroje a každý dáva výsledok s chybou. V najjednoduchšom prípade možno to, čo sme popísali, zredukovať na nasledujúci výraz: z = x + y, kde x je skutočná hodnota, ktorú chceme merať a ktorá by sa namerala, keby sme mali ideálne meracie zariadenie, y je zavedená chyba merania merací prístroj a z je hodnota, ktorú sme namerali. Úlohou Kalmanovho filtra je teda uhádnuť (určiť) podľa nameraného z, aká bola skutočná hodnota x, keď sme dostali naše z (v ktorom „sedí“ skutočná hodnota a chyba merania). Je potrebné odfiltrovať (odstrániť) skutočnú hodnotu x zo z - odstrániť skresľujúci šum y zo z. To znamená, že keď máme po ruke iba sumu, musíme uhádnuť, ktoré podmienky dali túto sumu.
Vo svetle vyššie uvedeného si teraz všetko sformulujme nasledujúcim spôsobom... Predpokladajme, že existujú iba dve náhodné čísla. Dostávame iba ich súčet a podľa tohto súčtu sme povinní určiť, aké sú podmienky. Napríklad sme dostali číslo 12 a hovoria: 12 je súčet čísel x a y, otázka je, čomu sa x a y rovnajú. Na zodpovedanie tejto otázky zostavíme rovnicu: x + y = 12. Dostali sme jednu rovnicu s dvoma neznámymi, preto, prísne vzaté, nie je možné nájsť dve čísla, ktoré by dali tento súčet. O týchto číslach si ale predsa len môžeme niečo povedať. Môžeme povedať, že to boli buď čísla 1 a 11, alebo 2 a 10, alebo 3 a 9, alebo 4 a 8, atď., tiež je to buď 13 a -1, alebo 14 a -2, alebo 15 a - 3 atď. To znamená, že súčtom (v našom príklade 12) môžeme určiť množinu možné možnosti ktorých súčet je presne 12. Jednou z týchto možností je pár, ktorý hľadáme a ktorý práve teraz dal 12. Za zmienku tiež stojí, že všetky možnosti pre dvojice čísel, ktoré tvoria súčet až 12, tvoria priamku znázornenú na obr. 1, ktorý je daný rovnicou x + y = 12 (y = -x + 12).

Obr

Dvojica, ktorú hľadáme, teda leží niekde na tejto priamke. Opakujem, je nemožné vybrať zo všetkých týchto možností tú dvojicu, ktorá v skutočnosti bola - ktorá dala číslu 12, bez toho, aby sme mali nejaké ďalšie stopy. Ale, v situácii, pre ktorú bol vynájdený Kalmanov filter, existujú také náznaky... Tam vopred o náhodné čísla niečo je známe. Známy je tam najmä takzvaný distribučný histogram pre každú dvojicu čísel. Zvyčajne sa získa po dosť dlhom pozorovaní výskytu týchto veľmi náhodných čísel. To znamená, že napríklad zo skúseností je známe, že v 5 % prípadov zvyčajne vypadne dvojica x = 1, y = 8 (túto dvojicu označujeme ako: (1,8)), v 2 % prípadov dvojica x = 2, y = 3 ( 2,3), v 1 % prípadov dvojica (3,1), v 0,024 % prípadov dvojica (11,1) atď. Opäť je nastavený tento histogram pre všetky páryčísla, vrátane tých, ktoré spolu tvoria 12. Teda pre každú dvojicu, ktorá dáva spolu 12, môžeme povedať, že napríklad dvojica (1, 11) vypadne v 0,8 % prípadov, dvojica ( 2, 10) - v 1% prípadov, pár (3, 9) - v 1,5% prípadov atď. Pomocou histogramu teda môžeme určiť, v akom percente prípadov je súčet členov páru 12. Predpokladajme, že napríklad v 30 % prípadov je súčet 12. A vo zvyšných 70 % padnú zvyšné páry von - to sú (1,8), (2, 3), (3,1) atď. - tie, ktorých súčet tvoria iné čísla ako 12. A nech napríklad dvojica (7,5) vypadne v 27 % prípadov, kým všetky ostatné dvojice, ktoré súčet do 12 vypadnú v 0,024 % + 0,8 % + 1 % + 1,5 % +… = 3 % prípadov. Podľa histogramu sme teda zistili, že čísla dávajúce spolu 12 vypadnú v 30% prípadov. Zároveň vieme, že ak padlo 12, tak najčastejšie (v 27 % z 30 %) je za tým dvojica (7,5). Teda ak už S vyvalenou 12-kou môžeme povedať, že v 90 % (27 % z 30 % - alebo, čo je rovnaké 27-krát z každých 30), dôvodom vyhodenej 12-ky je pár (7,5). S vedomím, že najčastejšie dôvodom na získanie sumy rovnajúcej sa 12 je pár (7,5), je logické predpokladať, že s najväčšou pravdepodobnosťou teraz vypadol. Samozrejme, stále nie je pravda, že v skutočnosti teraz číslo 12 tvorí práve tento pár, avšak nabudúce, ak narazíme na 12 a opäť predpokladáme pár (7,5), tak niekde v 90% prípadov na 100% budeme mat pravdu. Ale ak predpokladáme dvojicu (2, 10), potom budeme mať pravdu len v 1 % z 30 % prípadov, čo je 3,33 % správnych odhadov v porovnaní s 90 %, ak predpokladáme dvojicu (7,5). To je všetko - to je zmysel algoritmu Kalmanovho filtra. To znamená, že Kalmanov filter nezaručuje, že sa pri určovaní súčtu nepomýli, no garantuje, že sa pomýli minimálne toľkokrát (pravdepodobnosť chyby bude minimálna), keďže používa štatistiku - histogram chýbajúcich dvojíc čísel. Treba tiež zdôrazniť, že takzvaná hustota rozdelenia pravdepodobnosti (PDF) sa často používa v Kalmanovom filtračnom algoritme. Musíte však pochopiť, že význam je rovnaký ako význam histogramu. Histogram je navyše funkcia postavená na základe PDF a je jeho aproximáciou (pozri napr.).
V zásade môžeme tento histogram znázorniť ako funkciu dvoch premenných – teda ako plochu nad rovinou xy. Tam, kde je povrch vyšší, je väčšia pravdepodobnosť zodpovedajúceho páru. Obrázok 2 znázorňuje takýto povrch.

obr

Ako vidíte vyššie na priamke x + y = 12 (čo je variant párov, ktoré spolu dávajú 12), body povrchu sú umiestnené v rôznych výškach a najvyššej výške pre variant so súradnicami (7.5). A keď narazíme na sumu rovnajúcu sa 12, v 90% prípadov je dôvodom výskytu tejto sumy práve dvojica (7,5). Tie. práve táto dvojica, ktorá dáva spolu 12, má najvyššiu pravdepodobnosť výskytu, za predpokladu, že súčet je 12.
Preto je tu opísaná myšlienka Kalmanovho filtra. Práve na ňom sú postavené všetky druhy jeho modifikácií - jednokrokové, viackrokové rekurentné atď. Pre hlbšie štúdium Kalmanovho filtra odporúčam knihu: Van Tries G. Theory of detection, estimation and modulation.

p.s. Pre tých, ktorí majú záujem o vysvetlenie pojmov matematiky, čo sa nazýva „na prstoch“, môžete odporučiť túto knihu a najmä kapitoly z jej sekcie „Matematika“ (samotnú knihu alebo jednotlivé kapitoly si môžete zakúpiť na to).

• Návod

Na internete, vrátane Habrého, nájdete množstvo informácií o Kalmanovom filtri. Ťažko ale nájsť ľahko stráviteľný odvodenie samotných vzorcov. Bez záveru je celá táto veda vnímaná ako istý druh šamanizmu, vzorce vyzerajú ako anonymný súbor symbolov, a čo je najdôležitejšie, mnohé jednoduché tvrdenia, ktoré ležia na povrchu teórie, sú nepochopiteľné. Účelom tohto článku bude hovoriť o tomto filtri v čo najprístupnejšom jazyku.
Kalmanov filter je najmocnejší nástroj filtrovanie údajov. Jeho hlavným princípom je, že pri filtrovaní sa využívajú informácie o fyzike samotného javu. Ak napríklad filtrujete údaje z tachometra auta, zotrvačnosť auta vám dáva právo vnímať príliš rýchle skoky v rýchlosti ako chybu merania. Kalmanov filter je zaujímavý, pretože je v istom zmysle najviac najlepší filter... Nižšie si podrobnejšie rozoberieme, čo presne znamenajú slová „najlepší“. Na konci článku ukážem, že v mnohých prípadoch sa dajú vzorce zjednodušiť do takej miery, že z nich nezostane takmer nič.

Vzdelávací program

Pred zoznámením sa s Kalmanovým filtrom navrhujem zapamätať si niektoré jednoduché definície a fakty z teórie pravdepodobnosti.

Náhodná hodnota

Keď hovoria, že je daná náhodná premenná, myslia tým, že táto veličina môže trvať náhodné hodnoty... Má rôzne hodnoty s rôznymi pravdepodobnosťami. Keď hodíte povedzme kockou, vypadne diskrétny súbor hodnôt:. Kedy prichádza, napríklad o rýchlosti blúdiacej častice, potom sa samozrejme treba zaoberať súvislým súborom hodnôt. Budeme označovať „vypadnuté“ hodnoty náhodnej premennej prostredníctvom, ale niekedy použijeme rovnaké písmeno, ktoré označujeme náhodná premenná:
V prípade spojitej množiny hodnôt je náhodná premenná charakterizovaná hustotou pravdepodobnosti, ktorá nám diktuje, že pravdepodobnosť, že náhodná premenná „vypadne“ v malom okolí bodu s dĺžkou, je rovná. Ako vidíme z obrázku, táto pravdepodobnosť sa rovná ploche tieňovaného obdĺžnika pod grafom:

V živote sú náhodné premenné často gaussovské, keď je hustota pravdepodobnosti rovnaká.

Vidíme, že funkcia má tvar zvončeka centrovaného v bode a s charakteristickou šírkou rádu.
Keďže hovoríme o Gaussovom rozložení, bolo by hriechom nespomenúť, odkiaľ pochádza. Rovnako ako čísla sú pevne zavedené v matematike a nachádzajú sa na najneočakávanejších miestach, tak aj Gaussovo rozdelenie zapustilo hlboké korene v teórii pravdepodobnosti. Jedno pozoruhodné tvrdenie, ktoré čiastočne vysvetľuje Gaussovu všadeprítomnosť, je nasledovné:
Nech existuje náhodná premenná s ľubovoľným rozdelením (v skutočnosti existujú určité obmedzenia na túto svojvôľu, ale nie sú vôbec prísne). Vykonajte experimenty a vypočítajme súčet „vypadnutých“ hodnôt náhodnej premennej. Urobme veľa týchto experimentov. Je jasné, že zakaždým dostaneme inú hodnotu sumy. Inými slovami, tento súčet je sám osebe náhodnou premennou s vlastným istým distribučným zákonom. Ukazuje sa, že pre dostatočne veľký distribučný zákon tohto súčtu má tendenciu ku Gaussovmu rozdeleniu (mimochodom, charakteristická šírka "zvonca" rastie ako). Prečítajte si viac na Wikipédii: Centrálna limitná veta. V živote sa veľmi často vyskytujú množstvá, ktoré sa skladajú z Vysoké číslo identicky rozdelené nezávislé náhodné premenné sú preto rozdelené podľa Gaussovho princípu.

Priemerná

Priemerná hodnota náhodnej premennej je to, čo dostaneme v limite, ak vykonáme veľa experimentov a vypočítame aritmetický priemer vypadnutých hodnôt. Priemerná hodnota sa označuje rôznymi spôsobmi: matematici radi označujú cez (očakávanie alebo stredná hodnota) a zahraniční matematici cez (očakávanie). Fyzici sú cez resp. Cudzím spôsobom označíme:.
Napríklad pre Gaussovo rozdelenie je priemer.

Disperzia

V prípade Gaussovho rozdelenia jasne vidíme, že náhodná premenná uprednostňuje vypadnutie v určitej blízkosti svojej strednej hodnoty.

Opäť obdivujte Gaussovo rozdelenie

Ako je možné vidieť z grafu, charakteristický rozptyl hodnôt objednávky. Ako môžeme odhadnúť toto rozšírenie hodnôt pre ľubovoľnú náhodnú premennú, ak poznáme jej rozdelenie. Môžete nakresliť graf jeho hustoty pravdepodobnosti a odhadnúť charakteristickú šírku okom. Ale radšej ideme po algebraickej ceste. Môžete zistiť priemernú dĺžku (modul) odchýlky od priemeru:. Táto hodnota bude dobrým odhadom charakteristického rozptylu hodnôt. Ale vy a ja veľmi dobre vieme, že používanie modulov vo vzorcoch je jedno bolesť hlavy, preto sa tento vzorec zriedka používa na odhad charakteristického rozptylu.
Jednoduchší spôsob (jednoduchý z hľadiska výpočtov) je nájsť. Táto hodnota sa nazýva rozptyl a často sa označuje ako. Koreň rozptylu je dobrý odhad šírenia náhodnej premennej. Koreň rozptylu sa nazýva aj štandardná odchýlka.
Napríklad pre Gaussovo rozdelenie môžeme vypočítať, že rozptyl definovaný vyššie je presne rovnaký, čo znamená, že štandardná odchýlka je rovnaká, čo veľmi dobre súhlasí s našou geometrickou intuíciou.
V skutočnosti sa tu skrýva malý podvod. Faktom je, že v definícii Gaussovho rozdelenia je pod exponentom výraz. Táto dvojka v menovateli je práve preto, aby sa smerodajná odchýlka rovnala koeficientu. To znamená, že samotný vzorec Gaussovho rozdelenia je napísaný vo forme špeciálne upravenej tak, aby sme zvážili jeho štandardnú odchýlku.

Nezávislé náhodné premenné

Náhodné premenné sú závislé a nie. Predstavte si, že hodíte ihlu na rovinu a zapíšete súradnice oboch koncov. Tieto dve súradnice sú závislé, súvisia s tým, že vzdialenosť medzi nimi sa vždy rovná dĺžke ihly, hoci ide o náhodné hodnoty.
Náhodné premenné sú nezávislé, ak je výsledok prvej z nich úplne nezávislý od výsledku druhej z nich. Ak sú náhodné premenné nezávislé, potom sa priemerná hodnota ich súčinu rovná súčinu ich priemerných hodnôt:

Dôkaz

Napríklad mať modré oči a skončiť strednú školu so zlatou medailou sú nezávislé náhodné premenné. Ak modrookí, povedzme zlatí medailisti, potom modrookí medailisti. Tento príklad nám hovorí, že ak sú náhodné premenné dané ich hustotou pravdepodobnosti, potom nezávislosť týchto hodnôt je vyjadrená v skutočnosti, že hustota pravdepodobnosti ( prvá hodnota vypadla a druhá) sa zistí podľa vzorca:

Z toho hneď vyplýva, že:

Ako vidíte, dôkaz sa vykonáva pre náhodné premenné, ktoré majú spojité spektrum hodnôt a sú dané hustotou pravdepodobnosti. V iných prípadoch je myšlienka dôkazu podobná.

Kalmanov filter

Formulácia problému

Označme hodnotou, ktorú budeme merať a potom filtrujeme. Môžu to byť súradnice, rýchlosť, zrýchlenie, vlhkosť, zápach, teplota, tlak atď.
Začnime s jednoduchý príklad, čo nás privedie k formulácii spoločná úloha... Predstavte si, že máme rádiom riadené auto, ktoré môže jazdiť len tam a späť. Pri znalosti hmotnosti auta, tvaru, povrchu vozovky atď. sme vypočítali, ako ovládací joystick ovplyvňuje rýchlosť pohybu.

Potom sa súradnice auta zmenia podľa zákona:

V reálnom živote nemôžeme brať do úvahy pri výpočtoch malé poruchy pôsobiace na auto (vietor, hrbole, kamienky na ceste), preto skutočná rýchlosť stroj sa bude líšiť od vypočítaného. Na pravú stranu zapísanej rovnice sa pridá náhodná premenná:

Na písacom stroji máme nainštalovaný GPS senzor, ktorý sa snaží zmerať skutočné súradnice auta a, samozrejme, nevie to zmerať presne, ale meria to s chybou, ktorá je tiež náhodnou veličinou. Výsledkom je, že zo snímača dostávame chybné údaje:

Úlohou je, že pri znalosti nesprávnych hodnôt snímača nájdete dobrú aproximáciu skutočných súradníc auta. Túto dobrú aproximáciu budeme označovať ako.
Vo formulácii všeobecnej úlohy môže byť za súradnicu zodpovedné čokoľvek (teplota, vlhkosť ...) a výraz zodpovedný za riadenie systému zvonku bude označený (v príklade so strojom). Rovnice pre hodnoty súradníc a snímačov budú vyzerať takto:

(1)

Poďme diskutovať podrobne o tom, čo vieme:

Stojí za zmienku, že úloha filtrovania nie je úlohou vyhladzovania. Nesnažíme sa vyhladiť dáta zo snímača, snažíme sa dostať čo najbližšiu hodnotu k reálnej súradnici.

Kalmanov algoritmus

Budeme argumentovať indukciou. Predstavte si, že v kroku sme už našli filtrovanú hodnotu zo snímača, ktorá dobre aproximuje skutočné súradnice systému. Nezabudnite, že poznáme rovnicu, ktorá riadi zmenu neznámej súradnice:

Preto, keď ešte nedostaneme hodnotu zo snímača, môžeme predpokladať, že v jednom kroku sa systém vyvíja podľa tohto zákona a snímač bude ukazovať niečo blízke. Bohužiaľ, zatiaľ nevieme povedať nič presnejšie. Na druhej strane pri kroku budeme mať na rukách nepresné čítanie snímača.
Kalmanova myšlienka je, že na to, aby sme sa čo najlepšie priblížili skutočným súradniciam, musíme zvoliť strednú cestu medzi čítaním nepresného senzora a našou predpoveďou toho, čo sme od neho očakávali. Hodnote senzora priradíme váhu a váha zostane na predpokladanej hodnote:

Koeficient sa nazýva Kalmanov koeficient. Závisí od kroku iterácie, preto by bolo správnejšie ho napísať, no zatiaľ, aby sme nezaťažovali výpočtové vzorce, jeho index vynecháme.
Kalmanov koeficient musíme zvoliť tak, aby výsledná optimálna hodnota súradníc bola čo najbližšie k skutočnej súradnici. Napríklad, ak vieme, že náš senzor je veľmi presný, potom budeme jeho čítaniu viac dôverovať a hodnote prisúdime väčšiu váhu (blízko jednej). Ak je snímač naopak úplne nepresný, zameriame sa skôr na teoreticky predpovedanú hodnotu.
Vo všeobecnosti, aby ste našli presnú hodnotu Kalmanovho koeficientu, stačí minimalizovať chybu:

Na prepísanie výrazu pre chybu používame rovnice (1) (tie s modrým pozadím v rámčeku):

Dôkaz

Teraz je čas diskutovať o tom, čo znamená výraz minimalizovať chybu? Koniec koncov, chyba, ako vidíme, je sama o sebe náhodná premenná a zakaždým nadobúda iné hodnoty. V skutočnosti neexistuje univerzálny prístup k definovaniu toho, čo znamená, že chyba je minimálna. Tak ako v prípade rozptylu náhodnej veličiny, keď sme sa snažili odhadnúť charakteristickú šírku jej rozptylu, aj tu zvolíme najjednoduchšie kritérium pre výpočty. Minimalizujeme priemer druhej mocniny chyby:

Napíšme posledný výraz:

kľúč k dôkazu

Zo skutočnosti, že všetky náhodné premenné zahrnuté vo výraze pre sú nezávislé a priemerné hodnoty chýb snímača a modelu sa rovnajú nule:, vyplýva, že všetky „krížové“ členy sú rovné nule:
.
Vzorce rozptylu navyše vyzerajú oveľa jednoduchšie: a (keďže)

Tento výraz nadobúda minimálnu hodnotu, keď (deriváciu prirovnáme k nule)

Tu už píšeme výraz pre Kalmanov koeficient s indexom kroku, čím zdôrazňujeme, že závisí od kroku iterácie.
Do výrazu pre odmocninu dosadíme Kalmanov koeficient, ktorý ho minimalizuje. Dostaneme:

Naša úloha bola splnená. Získali sme iteračný vzorec na výpočet Kalmanovho koeficientu.

Všetky vzorce na jednom mieste

Príklad

Reklamný obrázok na začiatku článku filtruje údaje z fiktívneho GPS senzora nainštalovaného na fiktívnom aute, ktoré jazdí rovnomerne zrýchlene so známym fiktívnym zrýchlením.

Pozrite sa ešte raz na výsledok filtrovania

Matlab kód

zmazať všetko; N = 100 % počet vzoriek a = 0,1 % zrýchlenie sigmaPsi = 1 sigmaEta = 50; k = 1: N x = k x (1) = 0 z (1) = x (1) + normrnd (0, sigmaEta); pre t = 1: (N-1) x (t + 1) = x (t) + a*t + normrnd (0, sigmaPsi); z (t + 1) = x (t + 1) + normrnd (0, sigmaEta); koniec; % kalmanovho filtra xOpt (1) = z (1); eOpt (1) = sigmaEta; % eOpt (t) je druhá odmocnina rozptylu chýb (variancie). Nie je to náhodná premenná. Pre t = 1: (N-1) eOpt (t + 1) = sqrt ((sigmaEta ^ 2) * (eOpt (t) ^ 2 + sigmaPsi ^ 2) / (sigmaEta ^ 2 + eOpt (t) ^ 2 + sigmaPsi ^ 2)) K (t + 1) = (eOpt (t + 1)) ^ 2 / sigmaEta ^ 2 xOpt (t + 1) = (xOpt (t) + a * t ) * (1-K (t + 1)) + K (t + 1) * z (t + 1) koniec; graf (k, xOpt, k, z, k, x)

Analýza

Ak sledujeme, ako sa Kalmanov koeficient mení s krokom iterácie, môžeme ukázať, že sa vždy ustáli na určitej hodnote. Napríklad, keď sa rms chyby senzora a modelu navzájom týkajú ako desať ku jednej, potom graf Kalmanovho koeficientu v závislosti od kroku iterácie vyzerá takto:

V ďalšom príklade si povieme, ako nám to môže výrazne uľahčiť život.

Druhý príklad

V praxi sa často stáva, že o ničom nevieme fyzický modelčo filtrujeme. Napríklad chcete filtrovať hodnoty z vášho obľúbeného akcelerometra. Dopredu neviete, akým zákonom zamýšľate otočiť akcelerometer. Najviac informácií, ktoré môžete získať, je rozptyl chyby snímača. V takejto ťažkej situácii môže byť všetka neznalosť modelu pohybu privedená do náhodnej premennej:

Úprimne povedané, takýto systém vôbec nespĺňa podmienky, ktoré sme na náhodnú premennú uvalili, pretože teraz je tam skrytá všetka nám neznáma fyzika pohybu, a preto nemôžeme povedať, že model v rôznych časových okamihoch chyby sú na sebe nezávislé a ich stredné hodnoty sú nulové. V tomto prípade vo všeobecnosti nie je teória Kalmanovho filtra použiteľná. Nebudeme však venovať pozornosť tejto skutočnosti, ale hlúpo použijeme všetky kolosálne vzorce a vyberáme koeficienty podľa oka, takže filtrované údaje vyzerajú roztomilo.
Ale môžete ísť inak, oveľa viac ľahká cesta... Ako sme videli vyššie, Kalmanov koeficient sa vždy stabilizuje na hodnotu s rastúcim číslom kroku. Preto namiesto výberu koeficientov a hľadania Kalmanovho koeficientu pomocou zložitých vzorcov môžeme tento koeficient považovať za vždy konštantný a vybrať len túto konštantu. Tento predpoklad takmer nič nepokazí. Po prvé, už ilegálne používame Kalmanovu teóriu a po druhé, Kalmanov koeficient sa rýchlo ustáli na konštantu. Vo výsledku bude všetko veľmi zjednodušené. Vo všeobecnosti nepotrebujeme žiadne vzorce z Kalmanovej teórie, stačí nájsť prijateľnú hodnotu a vložiť ju do iteratívneho vzorca:

Nasledujúci graf ukazuje dva filtrované rôzne cestyúdaje z fiktívneho snímača. Za predpokladu, že nevieme nič o fyzike javu. Prvý spôsob je úprimný, so všetkými vzorcami z Kalmanovej teórie. A druhý je zjednodušený, bez vzorcov.

Ako vidíme, metódy sú takmer rovnaké. Malý rozdiel je pozorovaný len na začiatku, keď sa Kalmanov koeficient ešte nestabilizoval.

Diskusia

Ako sme videli, hlavnou myšlienkou Kalmanovho filtra je, že je potrebné nájsť taký koeficient, aby filtrovaná hodnota

V priemere by sa najmenej líšila od skutočnej hodnoty súradnice. Vidíme, že filtrovaná hodnota je lineárnou funkciou čítania senzora a predchádzajúcej filtrovanej hodnoty. A predchádzajúca filtrovaná hodnota je zase lineárna funkcia z načítania senzora a predchádzajúcej filtrovanej hodnoty. A tak ďalej, kým sa reťaz úplne nerozvinie. To znamená, že filtrovaná hodnota závisí od zo všetkých predchádzajúce hodnoty snímača lineárne:

Preto sa Kalmanov filter nazýva lineárny filter.
Dá sa dokázať, že Kalmanov filter je najlepší zo všetkých lineárnych filtrov. Najlepšie v tom zmysle, že stredná druhá mocnina chyby filtra je minimálna.

Viacrozmerný prípad

Celá teória Kalmanovho filtra sa dá zovšeobecniť na multidimenzionálny prípad. Vzorce tam vyzerajú trochu strašidelnejšie, ale samotná myšlienka ich odvodenia je rovnaká ako v jednorozmernom prípade. V tomto skvelom článku si ich môžete pozrieť:

Wienerove filtre sú najvhodnejšie pre procesy spracovania alebo úseky procesov vo všeobecnosti (blokové spracovanie). Pre sekvenčné spracovanie je potrebný aktuálny odhad signálu v každom taktovom cykle, berúc do úvahy informácie vstupujúce na vstup filtra počas procesu pozorovania.

Pri Wienerovom filtrovaní by si každá nová vzorka signálu vyžadovala prepočet váh všetkých filtrov. V súčasnosti rozšírené adaptívne filtre v ktorom prichádzajúci nové informácie slúži na priebežnú korekciu už vykonaného hodnotenia signálu (sledovanie cieľa v radare, automatické riadiace systémy v riadení atď.). Obzvlášť zaujímavé sú adaptívne filtre rekurzívneho typu známe ako Kalmanov filter.

Tieto filtre sú široko používané v regulačných slučkách v automatických regulačných a riadiacich systémoch. Odtiaľ sa objavili, o čom svedčí taká špecifická terminológia, ktorá sa používa na označenie ich práce ako štátneho priestoru.

Jednou z hlavných úloh, ktoré treba vyriešiť v praxi neurónových výpočtov, je získanie rýchlych a spoľahlivých algoritmov na učenie sa neurónových sietí. V tomto smere môže byť užitočné využitie v slučke spätná väzba trénovací algoritmus pre lineárne filtre. Keďže trénovacie algoritmy majú iteračný charakter, takýto filter musí byť sekvenčný rekurzívny odhad.

Problém odhadu parametrov

Jedna z úloh teórie štatistické rozhodnutia, ktoré majú veľký praktický význam, je problém posudzovania stavových vektorov a parametrov systémov, ktorý je formulovaný nasledovne. Predpokladajme, že je potrebné odhadnúť hodnotu parametra vektora $ X $, ktorý je pre priame meranie nedostupný. Namiesto toho sa meria iný parameter $ Z $ v závislosti od $ X $. Problémom odhadu je odpovedať na otázku: čo možno povedať o $ X $, keď vieme $ Z $. Vo všeobecnosti postup optimálneho hodnotenia vektora $ X $ závisí od akceptovaného kritéria kvality hodnotenia.

Napríklad Bayesovský prístup k problému odhadu parametrov vyžaduje úplnú a priori informáciu o pravdepodobnostných vlastnostiach odhadovaného parametra, čo je často nemožné. V týchto prípadoch sa uchyľujú k metóde najmenších štvorcov (OLS), ktorá vyžaduje oveľa menej a priori informácií.

Uvažujme o použití metódy najmenších štvorcov pre prípad, keď vektor pozorovania $ Z $ súvisí s vektorom odhadu parametra $ X $ lineárny model a v pozorovaní je interferencia $ V $, ktorá nekoreluje s odhadovaným parametrom:

$ Z = HX + V $, (1)

kde $ H $ je transformačná matica popisujúca vzťah medzi pozorovanými veličinami a odhadovanými parametrami.

Odhad $ X $ minimalizujúci druhú mocninu chyby je napísaný takto:

$ X_ (оц) = (H ^ TR_V ^ (- 1) H) ^ (- 1) H ^ TR_V ^ (- 1) Z $, (2)

Nech je interferencia $ V $ nekorelovaná, v tomto prípade je matica $ R_V $ jednoduchá matica identity a rovnica pre odhad sa stáva jednoduchšou:

$ X_ (ots) = (H ^ TH) ^ (- 1) H ^ TZ $, (3)

Písanie v matricovej forme výrazne šetrí papier, no pre niekoho to môže byť nezvyčajné. Toto všetko ilustruje nasledujúci príklad prevzatý z monografie Yu. M. Korshunova „Matematické základy kybernetiky“.
K dispozícii je nasledujúci elektrický obvod:

Pozorované hodnoty v v tomto prípade- údaje prístroja $ A_1 = 1 A, A_2 = 2 A, V = 20 B $.

Okrem toho je známy odpor $ R = 5 $ Ohm. Je potrebné hodnotiť najlepšia cesta, z hľadiska kritéria pre minimum strednej štvorcovej chyby, hodnoty prúdov $ I_1 $ a $ I_2 $. Najdôležitejšia vec je, že existuje určitý vzťah medzi pozorovanými hodnotami (údaje z prístroja) a odhadovanými parametrami. A tieto informácie sú privádzané zvonku.

V tomto prípade ide o Kirchhoffove zákony v prípade filtrácie (o ktorej bude toďalej) je autoregresný model časového radu, ktorý predpokladá závislosť aktuálnej hodnoty od predchádzajúcich.

Takže znalosť Kirchhoffových zákonov, ktorá nemá nič spoločné s teóriou štatistických rozhodnutí, umožňuje vytvoriť spojenie medzi pozorovanými hodnotami a odhadovanými parametrami (kto študoval elektrotechniku ​​- môže skontrolovať, zvyšok bude mať vziať ich za slovo):

$$ z_1 = A_1 = I_1 + \ xi_1 = 1 $$

$$ z_2 = A_2 = I_1 + I_2 + \ xi_2 = 2 $$

$$ z_2 = V / R = I_1 + 2 * I_2 + \ xi_3 = 4 $$

Je vo vektorovej forme:

$$ \ begin (vmatrix) z_1 \\ z_2 \\ z_3 \ end (vmatrix) = \ begin (vmatrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatrix) \ begin (vmatrix) I_1 \ \ I_2 \ end (vmatrix) + \ begin (vmatrix) \ xi_1 \\ \ xi_2 \\ \ xi_3 \ end (vmatrix) $$

Alebo $ Z = HX + V $, kde

$$ Z = \ begin (vmatrix) z_1 \\ z_2 \\ z_3 \ end (vmatrix) = \ begin (vmatrix) 1 \\ 2 \\ 4 \ end (vmatrix); H = \ begin (vmatica) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatica); X = \ begin (vmatrix) I_1 \\ I_2 \ end (vmatrix); V = \ begin (vmatrix) \ xi_1 \\ \ xi_2 \\ \ xi_3 \ end (vmatrix) $$

Ak vezmeme do úvahy navzájom nekorelované hodnoty interferencie, zistíme odhad I 1 a I 2 metódou najmenších štvorcov podľa vzorca 3:

$ H ^ TH = \ begin (vmatica) 1 & 1 & 1 \\ 0 & 1 & 2 \ end (vmatica) \ begin (vmatrix) 1 & 0 \\ 1 & 1 \\ 1 & 2 \ end (vmatica) = \ begin (vmatica) 3 & 3 \\ 3 & 5 \ end (vmatica); (H ^ TH) ^ (- 1) = \ frac (1) (6) \ begin (vmatica) 5 & -3 \\ -3 & 3 \ koniec (vmatica) $;

$ H ^ TZ = \ begin (vmatrix) 1 & 1 & 1 \\ 0 & 1 & 2 \ end (vmatrix) \ begin (vmatrix) 1 \\ 2 \\ 4 \ end (vmatrix) = \ begin (vmatrix) 7 \ \ 10 \ koniec (vmatica); X (ots) = \ frac (1) (6) \ begin (vmatrix) 5 & -3 \\ -3 & 3 \ end (vmatrix) \ begin (vmatrix) 7 \\ 10 \ end (vmatrix) = \ frac (1) (6) \ begin (vmatrix) 5 \\ 9 \ end (vmatrix) $;

Takže $ I_1 = 5/6 = 0,833 A $; $ I_2 = 9/6 = 1,5 A $.

Filtračná úloha

Na rozdiel od problému odhadovania parametrov, ktoré majú pevné hodnoty, v probléme filtrovania je potrebné odhadnúť procesy, teda nájsť aktuálne odhady časovo premenného signálu, skresleného rušením, a teda neprístupné priamemu meraniu. Vo všeobecnosti typ filtračných algoritmov závisí od štatistických vlastností signálu a šumu.

Budeme predpokladať, že užitočný signál je pomaly sa meniacou funkciou času a rušenie je nekorelovaný šum. Použijeme metódu najmenších štvorcov, opäť kvôli nedostatku apriórnych informácií o pravdepodobnostných charakteristikách signálu a rušení.

Najprv získame odhad aktuálnej hodnoty $ x_n $ za dostupné $ k $ posledné hodnotyčasový rad $ z_n, z_ (n-1), z_ (n-2) \ bodky z_ (n- (k-1)) $. Pozorovací model je rovnaký ako v probléme odhadu parametrov:

Je zrejmé, že $ Z $ je stĺpcový vektor pozostávajúci z pozorovaných hodnôt časového radu $ z_n, z_ (n-1), z_ (n-2) \ bodky z_ (n- (k-1)) $, $ V $ - vektorový stĺpec interferencie $ \ xi _n, \ xi _ (n-1), \ xi_ (n-2) \ bodky \ xi_ (n- (k-1)) $, skresľujúce skutočnú signál. Čo znamenajú symboly $ H $ a $ X $? O čom môžeme hovoriť napríklad o stĺpcovom vektore $ X $, ak je potrebné iba odhadnúť aktuálnu hodnotu časového radu? A čo znamená transformačná matica $ H $ nie je vôbec jasné.

Všetky tieto otázky môžu byť zodpovedané iba vtedy, ak sa vezme do úvahy koncept modelu generovania signálu. To znamená, že je potrebný nejaký model pôvodného signálu. Je to pochopiteľné, pri absencii apriórnych informácií o pravdepodobnostných charakteristikách signálu a rušení zostáva len predpokladať. Môžete to nazvať veštením z kávovej usadeniny, no odborníci uprednostňujú inú terminológiu. Na ich „féne“ sa tomu hovorí parametrický model.

V tomto prípade sa odhadujú parametre tohto konkrétneho modelu. Pri výbere vhodný model Pri generovaní signálu pamätajte, že akákoľvek analytická funkcia môže byť rozšírená v Taylorovom rade. Úžasnou vlastnosťou Taylorovho radu je, že tvar funkcie v ľubovoľnej konečnej vzdialenosti $ t $ od nejakého bodu $ x = a $ je jednoznačne určený správaním funkcie v nekonečne malom okolí bodu $ x = a $ (hovoríme o jeho derivátoch prvého a vyššieho rádu).

Existencia Taylorovho radu to znamená analytická funkcia má vnútorná štruktúra s veľmi silným putom. Ak sa napríklad obmedzíme na troch členov série Taylor, potom bude model generovania signálu vyzerať takto:

$ x_ (n-i) = F _ (- i) x_n $, (4)

$$ X_n = \ begin (vmatica) x_n \\ x "_n \\ x" "_ n \ koniec (vmatica); F _ (- i) = \ begin (vmatica) 1 & -i & i ^ 2/2 \\ 0 & 1 & -i \\ 0 & 0 & 1 \ koniec (vmatica) $$

To znamená, že vzorec 4 pre dané poradie polynómu (v príklade je to 2) vytvára spojenie medzi $ n $ -tou hodnotou signálu v časovej postupnosti a $ (n-i) $ -tou. Odhadovaný stavový vektor teda v tomto prípade zahŕňa okrem skutočnej odhadovanej hodnoty aj prvú a druhú deriváciu signálu.

V teórii automatického riadenia by sa takýto filter nazýval astatistický filter 2. rádu. Transformačná matica $ H $ pre tento prípad (odhad sa vykonáva na základe aktuálnych a $ k-1 $ predchádzajúcich vzoriek) vyzerá takto:

$$ H = \ begin (vmatica) 1 & -k & k ^ 2/2 \\ - & - & - \\ 1 & -2 & 2 \\ 1 & -1 & 0,5 \\ 1 & 0 & 0 \ koniec (vmatrix) $$

Všetky tieto čísla sú získané z Taylorovho radu za predpokladu, že časový interval medzi susednými pozorovanými hodnotami je konštantný a rovný 1.

Takže úloha filtrovania podľa našich predpokladov bola zredukovaná na úlohu odhadu parametrov; v tomto prípade sa odhadnú parametre prijatého modelu generovania signálu. A odhad hodnôt stavového vektora $ X $ sa vykonáva podľa rovnakého vzorca 3:

$$ X_ (ots) = (H ^ TH) ^ (- 1) H ^ TZ $$

V podstate sme implementovali proces parametrického odhadu založený na autoregresnom modeli procesu generovania signálu.

Vzorec 3 sa dá ľahko implementovať programovo, na to musíte vyplniť maticu $ H $ a vektorový stĺpec pozorovaní $ Z $. Tieto filtre sú tzv konečné pamäťové filtre, pretože používajú posledné pozorovania $ k $ na získanie aktuálneho odhadu $ X_ (nоц) $. Pri každom novom cykle pozorovaní sa k aktuálnemu súboru pozorovaní pridá nové a staré sa zahodí. Tento proces získavania známok sa nazýva posuvné okno.

Rastúce pamäťové filtre

Filtre s konečnou pamäťou majú hlavnú nevýhodu v tom, že po každom novom pozorovaní je potrebné znova vykonať kompletný prepočet všetkých údajov uložených v pamäti. Okrem toho výpočet odhadov možno spustiť až po nazhromaždení výsledkov prvých pozorovaní $ k $. To znamená, že tieto filtre majú dlhý prechodný čas.

Na boj proti tejto nevýhode je potrebné prejsť z filtra s trvalá pamäť filtrovať pomocou rastúca pamäť... V takomto filtri sa počet pozorovaných hodnôt, pre ktoré sa robí odhad, musí zhodovať s číslom n aktuálneho pozorovania. To umožňuje získať odhady začínajúce od počtu pozorovaní, ktorý sa rovná počtu zložiek odhadovaného vektora $ X $. A to je určené objednávkou prijatý model, teda koľko výrazov z Taylorovho radu je použitých v modeli.

Súčasne so zvyšujúcim sa n sa zlepšujú vyhladzovacie vlastnosti filtra, to znamená, že sa zvyšuje presnosť odhadov. Priama implementácia tohto prístupu je však spojená so zvýšením výpočtových nákladov. Preto sú rastúce pamäťové filtre implementované ako opakujúci.

Faktom je, že v čase n už máme odhad $ X _ ((n-1) оц) $, ktorý obsahuje informácie o všetkých predchádzajúcich pozorovaniach $ z_n, z_ (n-1), z_ (n-2) \ bodky z_ (n- (k-1)) $. Odhad $ X_ (nоц) $ sa získa z nasledujúceho pozorovania $ z_n $ pomocou informácií uložených v odhade $ X _ ((n-1)) (\ mbox (оц)) $. Tento postup sa nazýva rekurentné filtrovanie a pozostáva z nasledujúcich krokov:

• podľa odhadu $ X _ ((n-1)) (\ mbox (оц)) $ predpovedajte odhad $ X_n $ podľa vzorca 4 s $ i = 1 $: $ X _ (\ mbox (nоtsapriori)) = F_1X _ ((n-1) sc) $. Toto je a priori odhad;
• podľa výsledkov aktuálneho pozorovania $ z_n $ sa tento apriórny odhad prevedie na pravdivý, teda a posteriori;
• tento postup sa opakuje v každom kroku, počnúc od $ r + 1 $, kde $ r $ je poradie filtra.

Konečný vzorec pre opakované filtrovanie vyzerá takto:

$ X _ ((n-1) оц) = X _ (\ mbox (nоtsapriori)) + (H ^ T_nH_n) ^ (- 1) h ^ T_0 (z_n - h_0 X _ (\ mbox (nоtsapriori))) $ , (6)

kde pre náš filter druhej objednávky:

Rastúci pamäťový filter fungujúci podľa Formuly 6 - špeciálny prípad filtračný algoritmus známy ako Kalmanov filter.

o praktickú realizáciu tohto vzorca treba pripomenúť, že apriórny odhad, ktorý je v ňom zahrnutý, je určený vzorcom 4 a hodnota $ h_0 X _ (\ mbox (notsapriori)) $ je prvou zložkou vektora $ X _ (\ mbox (notsapriori)) $.

Rastúci pamäťový filter má jeden dôležitá vlastnosť... Ak sa pozriete na vzorec 6, potom konečné skóre je súčtom predpokladaného vektora skóre a opravného člena. Táto korekcia je veľká pre malé $ n $ a znižuje sa so zvyšujúcim sa $ n $, pričom má tendenciu k nule ako $ n \ šípka doprava \ infty $. To znamená, že s nárastom n rastú vyhladzovacie vlastnosti filtra a začína dominovať model, ktorý je mu vlastný. ale skutočný signál môže zodpovedať modelu len v určitých oblastiach, preto sa presnosť prognózy zhoršuje.

Aby sa tomu zabránilo, od niektorých $ n $ sa ukladá zákaz ďalšieho znižovania opravného termínu. To je ekvivalentné zmene šírky pásma filtra, to znamená, že pre malé n je filter širší (menej inerciálny), pre veľké n sa stáva viac zotrvačným.

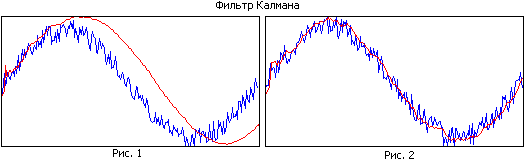
Porovnajte obrázok 1 a obrázok 2. Na prvom obrázku má filter skvelá pamäť, síce dobre vyhladzuje, no kvôli úzkemu pásmu odhadovaná dráha zaostáva za skutočnou. Na druhom obrázku je pamäť filtra menšia, horšie sa vyhladzuje, ale lepšie sleduje skutočnú trajektóriu.

Literatúra

1. YM Korshunov "Matematické základy kybernetiky"
2. A.V. Balakrishnan "Kalmanova teória filtrácie"
3. V.N.Fomin „Opakujúci sa odhad a adaptívne filtrovanie"
4. C.F.N. Cowen, P.M. Udeliť „Adaptívne filtre“