Đăng ký dịch chuyển phản hồi tuyến tính(RSLOS, tương tác thanh ghi dịch chuyển phản hồi tuyến tính, LFSR) là một thanh ghi dịch chuyển của các từ bit, trong đó giá trị của bit đầu vào (trượt) bằng một hàm Boolean tuyến tính từ các giá trị của các bit còn lại của thanh ghi trước khi dịch chuyển. Nó có thể được tổ chức bởi cả phần mềm và phần cứng. Nó được sử dụng để tạo ra các bit chuỗi giả ngẫu nhiên, đặc biệt, được sử dụng trong mật mã.
Sự miêu tả
Điều khiển thanh ghi trong triển khai phần cứng được thực hiện bằng cách áp dụng một xung dịch chuyển (cách gọi khác đồng hồ hoặc là đồng bộ xung) cho tất cả các ô. Quản lý đăng ký trong triển khai phần mềm được thực hiện bằng cách thực hiện một vòng lặp. Tại mỗi lần lặp của vòng lặp, hàm phản hồi được tính toán và dịch chuyển các bit trong từ.
Nguyên lý hoạt động
Độ phức tạp tuyến tính
Tương quan Độc lập
Trong một nỗ lực để có được độ phức tạp tuyến tính cao của chuỗi được tạo, các nhà mật mã kết hợp không tuyến tính các đầu ra của một số thanh ghi dịch chuyển. Trong trường hợp này, một hoặc nhiều chuỗi đầu ra (hoặc thậm chí đầu ra của các LFSR riêng lẻ) có thể được kết nối bằng một luồng chung và được mở bởi một nhà phân tích mật mã. Hacking dựa trên một lỗ hổng như vậy được gọi là mở tương quan. Ý tưởng chính của một vụ hack như vậy là để tìm một số mối tương quan giữa đầu ra của máy phát điện và đầu ra của các bộ phận thành phần của nó. Sau đó, bằng cách quan sát trình tự đầu ra, người ta có thể có được thông tin về các đầu ra trung gian này, và do đó hack bộ tạo. Thomas Siegenthaler đã chỉ ra rằng có thể xác định chính xác tính độc lập tương quan và có sự đánh đổi giữa tính độc lập tương quan và độ phức tạp tuyến tính.
Triển khai phần mềm
Phần mềm triển khai RSLOS khá chậm và hoạt động nhanh hơn nếu chúng được viết bằng trình hợp dịch. Một trong những giải pháp là sử dụng song song 16 RLLS (hoặc 32, tùy thuộc vào độ dài từ trong kiến trúc máy tính). Trong một lược đồ như vậy, một mảng các từ được sử dụng, kích thước của nó bằng độ dài của thanh ghi dịch chuyển và mỗi bit của từ này tham chiếu đến LFSR của chính nó. Vì cùng một số lượng trình tự vòi được sử dụng, điều này có thể mang lại mức tăng đáng kể trong hiệu suất của máy phát.
Cấu hình Fibonacci
Hãy xem xét một thanh ghi dịch chuyển 32-bit. Nó có một trình tự thoát (32, 31, 30, 28, 26, 1) (\ displaystyle \ left (32, \; 31, \; 30, \; 28, \; 26, \; 1 \ right)). Điều này có nghĩa là để tạo ra một bit mới, cần phải tính tổng các bit thứ 31, 30, 29, 27, 25 và 0 bằng phép toán XOR. LFSR kết quả có khoảng thời gian tối đa 2 32 - 1 (\ displaystyle 2 ^ (32) -1). Mã cho một thanh ghi như vậy trong C như sau:
int LFSR_Fibonacci (void) (static unsigned long S = 0x00000001; S = (((((S >> 31) ^ (S >> 30) ^ (S >> 29) ^ (S >> 27) ^ (S >> 25) ^ S) & 0x00000001)<< 31 ) | (S >> 1); trả về S & 0x00000001; )
Cấu hình Galois
Trình tạo này không có sức mạnh mật mã lớn hơn, nhưng nó mang lại hiệu suất tăng: tất cả các hoạt động XOR có thể được thực hiện trong một hoạt động thông qua song song hóa và không tuần tự lần lượt như trong cấu hình Fibonacci. Đề án này cũng sẽ mang lại lợi ích trong việc triển khai phần cứng.
Mã cho thanh ghi dịch chuyển 32-bit trong C như sau:
int LFSR_Galois (void) (static unsigned long S = 0x00000001; if (S & 0x00000001) (S = (S ^ 0x80000057 >> 1) | 0x80000000; return 1;) else (S >> = 1; return 0;))
Cần lưu ý rằng vòng lặp của một số lượng cố định lệnh gọi hàm LFSR_Galois trong cấu hình Galois được thực thi nhanh hơn khoảng 2 lần so với hàm LFSR_Fibonacci trong cấu hình Fibonacci (trình biên dịch MS VS 2010 trên Intel Core i5).
Ví dụ về trình tự đã tạo
Cấu hình Fibonacci
Hãy để LFSR được cho bởi đa thức đặc trưng x 3 + x + 1 (\ displaystyle x ^ (3) + x + 1). Điều này có nghĩa là các bit vòi sẽ là thứ 2 và 0, và đơn vị trong công thức đa thức có nghĩa là bit thứ 0 là đầu vào. Chức năng phản hồi có dạng S j = S j - 1 ⊕ S j - 3 (\ displaystyle S_ (j) = S_ (j-1) \ oplus S_ (j-3)). Giả sử trạng thái ban đầu của thanh ghi shift là chuỗi. Các trạng thái khác của thanh ghi được hiển thị trong bảng dưới đây:
| Số bước | Trạng thái | Bit được tạo |
|---|---|---|
| 0 | [0, 0, 1] (\ displaystyle \ left) | 1 |
| 1 | 0 | |
| 2 | 0 | |
| 3 | 1 | |
| 4 | 1 | |
| 5 | 1 | |
| 6 | 0 | |
| 7 | [0, 0, 1] (\ displaystyle \ left) | 1 |
Vì trạng thái bên trong ở bước thứ bảy trở lại trạng thái ban đầu, nên bắt đầu từ bước tiếp theo, các bit sẽ được lặp lại. Vì vậy, trình tự được tạo là: [1, 0, 0, 1, 1, 1, 0, 1. . . ] (\ displaystyle \ left)(thứ tự của các bit trong chuỗi tương ứng với thứ tự mà chúng được tạo bởi LFSR). Do đó, chu kỳ của dãy là 7, tức là giá trị lớn nhất có thể, đã xảy ra do tính nguyên thủy của đa thức đã cho.
Cấu hình Galois
Chúng ta hãy lấy một đa thức đặc trưng giống nhau, đó là, c 3 = c 1 = 1 (\ displaystyle c_ (3) = c_ (1) = 1), c2 = 0 (\ displaystyle c_ (2) = 0). Chỉ có bit đầu tiên được thêm vào bit đầu ra. Trạng thái ban đầu giống nhau. Các trạng thái khác của sổ đăng ký:
| Số bước | Trạng thái | Bit được tạo |
|---|---|---|
| 0 | [0, 0, 1] (\ displaystyle \ left) | - |
| 1 | [1, 0, 0] (\ displaystyle \ left) | 0 |
| 2 | [0, 1, 1] (\ displaystyle \ left) | 1 |
| 3 | [1, 0, 1] (\ displaystyle \ left) | 1 |
| 4 | [1, 1, 1] (\ displaystyle \ left) | 1 |
| 5 | [1, 1, 0] (\ displaystyle \ left) | 0 |
| 6 | [0, 1, 0] (\ displaystyle \ left) | 0 |
| 7 | [0, 0, 1] (\ displaystyle \ left) | 1 |
Trạng thái bên trong của thanh ghi ở bước thứ bảy trở lại trạng thái ban đầu, do đó, chu kỳ của nó cũng bằng 7. Không giống như cấu hình Fibonacci, các trạng thái bên trong của thanh ghi hóa ra khác nhau, nhưng trình tự được tạo ra thì giống nhau. , chỉ được dịch chuyển bởi 4 chu kỳ: [0, 1, 1, 1, 0, 0, 0, 0, 1, 1 ,. . . ] (\ displaystyle \ left)(thứ tự của các bit trong chuỗi tương ứng với thứ tự mà chúng được tạo bởi LFSR).
Tạo đa thức nguyên thủy
| chút ít, n (\ displaystyle n) | Đa thức nguyên thủy | Giai đoạn = Stage, 2 n - 1 (\ displaystyle 2 ^ (n) -1) | Số đa thức nguyên thủy |
|---|---|---|---|
| 2 | x 2 + x + 1 (\ displaystyle x ^ (2) + x + 1) | 3 | 1 |
| 3 | x 3 + x 2 + 1 (\ displaystyle x ^ (3) + x ^ (2) +1) | 7 | 2 |
| 4 | x 4 + x 3 + 1 (\ displaystyle x ^ (4) + x ^ (3) +1) | 15 | 2 |
| 5 | x 5 + x 3 + 1 (\ displaystyle x ^ (5) + x ^ (3) +1) | 31 | 6 |
| 6 | x 6 + x 5 + 1 (\ displaystyle x ^ (6) + x ^ (5) +1) | 63 | 6 |
| 7 | x 7 + x 6 + 1 (\ displaystyle x ^ (7) + x ^ (6) +1) | 127 | 18 |
| 8 | x 8 + x 6 + x 5 + x 4 + 1 (\ displaystyle x ^ (8) + x ^ (6) + x ^ (5) + x ^ (4) +1) | 255 | 16 |
| 9 | x 9 + x 5 + 1 (\ displaystyle x ^ (9) + x ^ (5) +1) | 511 | 48 |
| 10 | x 10 + x 7 + 1 (\ displaystyle x ^ (10) + x ^ (7) +1) | 1023 | 60 |
| 11 | x 11 + x 9 + 1 (\ displaystyle x ^ (11) + x ^ (9) +1) | 2047 | 176 |
| 12 | x 12 + x 11 + x 10 + x 4 + 1 (\ displaystyle x ^ (12) + x ^ (11) + x ^ (10) + x ^ (4) +1) | 4095 | 144 |
| 13 | x 13 + x 12 + x 11 + x 8 + 1 (\ displaystyle x ^ (13) + x ^ (12) + x ^ (11) + x ^ (8) +1) | 8191 | 630 |
| 14 | x 14 + x 13 + x 12 + x 2 + 1 (\ displaystyle x ^ (14) + x ^ (13) + x ^ (12) + x ^ (2) +1) | 16383 | 756 |
| 15 | x 15 + x 14 + 1 (\ displaystyle x ^ (15) + x ^ (14) +1) | 32767 | 1800 |
| 16 | x 16 + x 14 + x 13 + x 11 + 1 (\ displaystyle x ^ (16) + x ^ (14) + x ^ (13) + x ^ (11) +1) | 65535 | 2048 |
| 17 | x 17 + x 14 + 1 (\ displaystyle x ^ (17) + x ^ (14) +1) | 131071 | 7710 |
| 18 | x 18 + x 11 + 1 (\ displaystyle x ^ (18) + x ^ (11) +1) | 262143 | 7776 |
| 19 | x 19 + x 18 + x 17 + x 14 + 1 (\ displaystyle x ^ (19) + x ^ (18) + x ^ (17) + x ^ (14) +1) | 524287 | 27594 |
| 20 - 168 | |||
| 2 - 786, 1024, 2048, 4096 | |||
Ưu điểm và nhược điểm
Thuận lợi
- hiệu suất cao của các thuật toán mật mã được tạo trên cơ sở LFSR (ví dụ: mật mã dòng);
- chỉ sử dụng các phép toán bit đơn giản nhất của phép cộng và phép nhân, được thực hiện trong phần cứng của hầu hết các thiết bị máy tính;
- các thuộc tính mật mã tốt (LFSR có thể tạo ra các chuỗi chu kỳ dài với các đặc tính thống kê tốt);
- do cấu trúc của chúng, các LFSR dễ dàng được phân tích bằng phương pháp đại số.
Flaws
Các cách để cải thiện sức mạnh mật mã của các chuỗi được tạo
Máy phát điện với nhiều thanh ghi dịch chuyển
Loại bộ tạo này bao gồm một số thanh ghi dịch chuyển phản hồi tuyến tính tạo ra các bit x 1, i, x 2, i,…, x M, i (\ displaystyle x_ (1, i), \; x_ (2, i), \; \ dot, \; x_ (M, i)) tương ứng. Hơn nữa, các bit được tạo ra được biến đổi bởi một số hàm boolean f (x 1, i, x 2, i,…, x M, i) (\ displaystyle f (x_ (1, i), \; x_ (2, i), \; \ dot, \; x_ (M ,tôi))). Cần lưu ý rằng các trình tạo kiểu này có độ dài thanh ghi L i (\ displaystyle L_ (i)), i = 1, 2,…, M (\ displaystyle i = 1, \; 2, \; \ dot, \; M), là đồng chuẩn với nhau.
Thời kỳ của máy phát điện này là T = (2 L 1 - 1) ⋅ (2 L 2 - 1) ⋯ (2 LM - 1) ≲ 2 L (\ displaystyle T = (2 ^ (L_ (1)) - 1) \ cdot (2 ^ ( L_ (2)) - 1) \ cdots (2 ^ (L_ (M)) - 1) \ lesssim 2 ^ (L)), ở đâu L = ∑ i = 1 M L i (\ displaystyle L = \ sum \ limit _ (i = 1) ^ (M) L_ (i))- tổng số ô. Do đó, việc sử dụng một số LFSR làm tăng chu kỳ của chuỗi được tạo so với một thanh ghi đơn lẻ, điều này làm tăng độ bền mật mã của trình tạo. Nó cũng làm tăng độ phức tạp tuyến tính hoặc độ dài của thanh ghi ngắn nhất tương ứng với một bộ tạo nhất định. Một thanh ghi như vậy được tìm thấy bằng cách sử dụng thuật toán Berlekamp-Massey sử dụng trình tự đã tạo. Tốt nhất, độ dài của nó phải tương xứng với khoảng thời gian của chuỗi được tạo.
Máy phát điện có phép biến đổi phi tuyến tính
Sơ đồ khối của máy phát điện như vậy không khác gì sơ đồ của máy phát điện trước đó. Sự khác biệt chính là thiết bị biến đổi được cung cấp bởi một hàm Boolean phi tuyến tính f (x 1, x 2,…, x M) (\ displaystyle f (x_ (1), x_ (2), \ dot, x_ (M))). Ví dụ, đa thức Zhegalkin được coi là một hàm như vậy (theo định lý Zhegalkin, bất kỳ hàm Boolean nào có thể được biểu diễn duy nhất bởi đa thức Zhegalkin).
Một bộ tạo phi tuyến cũng có thể được triển khai trên thanh ghi dịch chuyển phản hồi phi tuyến tính. Anh ấy có thể cho 2 2 L - 1 - L (\ displaystyle 2 ^ (2 ^ (L-1) -L)) các biến thể của chu kỳ tối đa của chuỗi, nhiều hơn của LFSR.
Độ bền mật mã của trình tạo này được tăng lên do tính phi tuyến tính của hàm được sử dụng. Việc xác định trạng thái của các thanh ghi từ chuỗi bit được tạo ra là một vấn đề toán học phức tạp, bởi vì không có thuật toán nào khôi phục lại các trạng thái ban đầu.
Ví dụ, phương pháp này được sử dụng trong máy phát điện Geff và bộ tạo Geff tổng quát, tuy nhiên, những bộ tạo như vậy có thể bị phá vỡ bởi một cuộc tấn công tương quan.
Máy phát điện có thời gian đăng ký dịch chuyển khác nhau
máy phát điện dừng lại
máy phát điện dừng lại(Tiếng Anh Stop-and-Go, Both-Piper) sử dụng đầu ra của LFOS-1 để điều khiển tần số xung nhịp của LFOS-2, để LFSR-2 thay đổi trạng thái của nó tại một số thời điểm chỉ khi đầu ra của LFOS-1 tại thời điểm đó là bằng đơn vị. Đề án này đã không chống lại sự mở ra tương quan.
Để tăng sức mạnh mật mã, nó đã được đề xuất máy phát điện dừng và chạy. Nó sử dụng ba thanh ghi dịch chuyển có độ dài khác nhau. Ở đây, LFOS-1 điều khiển tần số xung nhịp của thanh ghi thứ 2 và thứ 3, nghĩa là, LFSR-2 thay đổi trạng thái của nó khi đầu ra LFSR-1 bằng một và LFSR-3 - khi đầu ra LFSR-1 bằng số không. Đầu ra của bộ tạo là hoạt động thêm modulo hai đầu ra RSLOS-2 và RSLOS-3. Máy phát điện này có chu kỳ lớn và độ phức tạp tuyến tính lớn. Có một phương pháp mở tương quan của RLOS-1, nhưng điều này không làm suy yếu đáng kể các thuộc tính mật mã của trình tạo.
Một sơ đồ đồng hồ phức tạp được sử dụng trong máy phát điện dừng và đi hai chiều, trong đó sử dụng 2 thanh ghi dịch chuyển có cùng độ dài. Nếu đầu ra của RLOS-1 tại một thời điểm nào đó t i - 1 (\ displaystyle t_ (i-1))- một, thì RLOS-2 không có xung nhịp tại thời điểm đó t i (\ displaystyle t_ (i)). Nếu đầu ra của RLOS-2 tại thời điểm t i - 1 (\ displaystyle t_ (i-1)) bằng 0 và tại thời điểm t i - 2 (\ displaystyle t_ (i-2))- một, và nếu thanh ghi này được đồng hồ vào thời điểm đó t i (\ displaystyle t_ (i)), thì tại cùng thời điểm RLOS-1 không được xung nhịp. Độ phức tạp tuyến tính của mạch này xấp xỉ bằng chu kỳ của chuỗi được tạo ra.
Máy phát điện tự phân tách
Đa dao động với sản phẩm bên trong
Bộ tạo này sử dụng hai thanh ghi dịch chuyển RSLOS-1 và RSLOS-2. Tần số đồng hồ của RSLOS-2 trong d (\ displaystyle d) gấp nhiều lần so với RSLOS-1. Các bit nhất định của các thanh ghi này được nhân với nhau bằng phép toán AND. Kết quả của các phép nhân được thêm vào bằng phép toán XOR và thu được chuỗi đầu ra. Bộ tạo này có độ phức tạp tuyến tính cao và có các đặc tính thống kê tốt. Tuy nhiên, trạng thái của nó có thể được xác định từ một chuỗi đầu ra có độ dài L 1 + L 2 + log 2 d (\ displaystyle L_ (1) + L_ (2) + \ log _ (2) (d)), ở đâu L 1 (\ displaystyle L_ (1)) và L 2 (\ displaystyle L_ (2)) lần lượt là độ dài của LFOS-1 và LFOS-2, và d (\ displaystyle d)- tỷ lệ tần số đồng hồ của chúng.
Gollmann Cascade
Mạch này là một phiên bản cải tiến của bộ tạo dừng. Nó bao gồm một chuỗi các LFSR, thời gian của mỗi trong số đó được kiểm soát bởi LFSR trước đó. Nếu đầu ra của RLOS-1 tại thời điểm t i (\ displaystyle t_ (i)) là 1, thì RLOS-2 được xung nhịp. Nếu đầu ra của RLOS-2 tại thời điểm t i (\ displaystyle t_ (i)) là 1, thì RLOS-3 được tăng xung nhịp, v.v. Đầu ra của LFSR cuối cùng là đầu ra của bộ tạo. Nếu độ dài của tất cả các LFSR là như nhau và bằng L (\ displaystyle L), sau đó khoảng thời gian của hệ thống từ M (\ displaystyle M) LFSR bằng (2 L - 1) M (\ displaystyle (2 ^ (L) -1) ^ (M)) và độ phức tạp tuyến tính là L (S) = L (2 L - 1) M - 1 (\ displaystyle L (S) = L (2 ^ (L) -1) ^ (M-1)) .
Ý tưởng này rất đơn giản và có thể được sử dụng để tạo ra các chuỗi có chu kỳ lớn, độ phức tạp tuyến tính lớn và các thuộc tính thống kê tốt. Nhưng, thật không may, chúng rất nhạy cảm với một cuộc khám nghiệm tử thi được gọi là khóa(khóa tương tác) khi
- "Quần vợt Tetromino"). Ông đã tạo ra và giải quyết vô số câu đố toán học và chơi chữ. Khoảng 20 năm trước, tôi biết rằng anh ấy đã tiến rất gần đến việc khám phá ra quy tắc yêu thích của tôi là 30 cho ô tô tự động vào năm 1959, khi tôi vừa mới sinh ra.
Làm thế nào tôi gặp Saul Golomb
Hầu hết tất cả các nhà khoa học và nhà toán học mà tôi biết, tôi đều biết thông qua các mối quan hệ chuyên môn của mình. Nhưng không phải Sol Golomba. Đó là năm 1981, và tôi, một nhà vật lý 21 tuổi (người đã phần nào trở nên nổi tiếng trên các phương tiện truyền thông vì tôi là người trẻ nhất nhận Giải thưởng MacArthur tại lễ trao giải đầu tiên) đang nghiên cứu. Có tiếng gõ cửa văn phòng của tôi, và ngay sau đó một phụ nữ trẻ bước qua ngưỡng cửa. Điều này vốn đã bất thường, bởi vì trong những ngày đó, nơi họ tham gia vào lĩnh vực vật lý năng lượng cao lý thuyết, chỉ có rất ít phụ nữ. Mặc dù tôi đã sống ở California trong vài năm, tôi chưa bao giờ rời khỏi khuôn viên trường đại học, và do đó, tôi không chuẩn bị tốt cho làn sóng năng lượng Nam California tràn vào văn phòng của tôi. Người phụ nữ này tự giới thiệu mình là Astrid và nói rằng cô ấy đã học ở Oxford và biết một người mà tôi đã học cùng ở trường mẫu giáo. Cô giải thích rằng cô đã được giao nhiệm vụ thu thập thông tin về những người thú vị trong khu vực Pasadena. Tôi nghĩ cô ấy coi tôi là một ca khó, nhưng vẫn nhất quyết không chịu nói chuyện. Và một ngày, khi tôi đang cố gắng kể điều gì đó về những gì tôi làm, cô ấy nói: " Bạn phải gặp cha tôi. Ông ta đã là một ông già, nhưng tâm trí ông ta vẫn còn sắc như dao cạo. Và điều đó thật xảy ra khi Astrid Golomb, con gái lớn của Sol Golomb, đã giới thiệu tôi với anh ấy.Gia đình Golomb sống trong một ngôi nhà nằm trên núi gần Pasadena. Họ có hai cô con gái: Astrid, lớn hơn tôi một chút, một cô gái Hollywood đầy tham vọng, và Beatrice, bằng tuổi tôi và đầu óc khoa học. Hai chị em nhà Golomb thường tổ chức các bữa tiệc - thường là tại nhà của họ. Các chủ đề dao động từ một bữa tiệc trong vườn đến quây quần với hồng hạc và nhím (" Người chiến thắng sẽ là người có trang phục phù hợp nhất với chủ đề đã nêu."), hoặc một bữa tiệc theo phong cách Stonehenge với những hướng dẫn được viết bằng chữ rune. Những người trẻ tuổi và không quá trẻ đã giao nhau trong những bữa tiệc này, bao gồm các ánh sáng địa phương khác nhau. Và ở họ, một chút sang một bên, luôn có một người đàn ông nhỏ bé với một bộ râu lớn, hơi giống trên một yêu tinh và người luôn mặc một chiếc áo khoác sẫm màu - chính là Solomon Golomb.
Dần dần tôi biết một chút về anh ấy. Những gì anh ấy đã tham gia vào " lý thuyết thông tin"Đó là anh ấy làm việc tại Đại học Nam California. Anh ấy có nhiều mối quan hệ mơ hồ nhưng rõ ràng là cấp cao với chính phủ và các mối quan hệ khác. Tôi đã nghe nói về sổ đăng ký thay đổi, nhưng hầu như không biết gì về chúng.

Đây là những gì sẽ xảy ra sau một thời gian:

Như bạn có thể thấy, thanh ghi shift luôn dịch chuyển các bit sang trái và các bit khác được thêm vào bên phải theo một quy tắc đơn giản. Chuỗi các bit dường như là ngẫu nhiên, mặc dù, như thể hiện trong hình, cuối cùng nó lặp lại chính nó. Saul Golomb đã tìm ra một phương pháp toán học thanh lịch để phân tích các chuỗi như vậy và cách chúng tự lặp lại.
Nếu thanh ghi ca có kích thước n, sau đó anh ấy có 2 n các trạng thái có thể có (tương ứng với tất cả các chuỗi có thể có 0 và 1 với độ dài n). Vì các quy tắc cho thanh ghi dịch chuyển là xác định, bất kỳ vị trí nhất định nào phải luôn đến vị trí khác như vậy. Và điều này có nghĩa là số bước tối đa có thể có mà thanh ghi shift có thể trải qua trước khi các bước bắt đầu lặp lại là 2 n(thực ra là 2 n- 1, vì một vị trí có tất cả các số 0 không thể phát triển thành bất kỳ thứ gì khác).
Trong ví dụ trên, thanh ghi shift có kích thước là 7 và sẽ lặp lại chính xác 2 bước 7 - 1 = 127. Nhưng thanh ghi dịch chuyển nào - với các vị trí vòi nào - sẽ tạo ra các chuỗi có độ dài tối đa? Solomon Golomb bắt đầu điều tra câu hỏi này vào mùa hè năm 1954. Và câu trả lời của anh ấy rất đơn giản và tao nhã.
Thanh ghi shift ở trên có các vòi ở vị trí 7, 6 và 1. Saul đã biểu diễn đại số này bằng cách sử dụng đa thức X 7 + X 6 + 1. Sau đó, anh ấy chỉ ra rằng dãy được tạo ra sẽ có độ dài tối đa nếu đa thức này " modulo không thể thay đổi 2"; do đó, nó không thể được nhân tử hóa, điều này làm cho nó giống như một số nguyên tố trong số các đa thức; và sự hiện diện của một số thuộc tính khác khiến nó trở thành" đa thức nguyên thủy ". Ngày nay, điều này dễ dàng kiểm tra bằng cách sử dụng Mathematica và Wolfram Language:
Sau đó, vào năm 1954, Sau-lơ phải làm tất cả bằng tay; ông đã biên soạn một bảng khá dài gồm các đa thức nguyên thủy tương ứng với các thanh ghi shift, tạo ra các chuỗi có độ dài tối đa:

Lịch sử của sổ đăng ký ca
Ý tưởng duy trì RAM thông qua " đường trễ", truyền xung kỹ thuật số, có từ đầu kỷ nguyên máy tính. Vào cuối những năm 1940, những đường trễ như vậy đã được áp dụng kỹ thuật số bằng cách sử dụng một loạt các ống chân không và được gọi là" sổ đăng ký thay đổi Vẫn chưa rõ khi nào các thanh ghi dịch chuyển phản hồi đầu tiên được tạo ra. Nó có thể là vào cuối những năm 1940. Tuy nhiên, sự kiện này vẫn bị che đậy trong bí ẩn vì chúng lần đầu tiên được sử dụng trong mật mã quân sự.Ý tưởng cơ bản của mật mã là thay đổi các thông điệp có ý nghĩa theo cách mà chúng không thể được nhận ra; tuy nhiên, nếu bạn biết khóa, bạn có thể tạo lại tin nhắn đã mã hóa. Cái gọi là mật mã dòng hoạt động trên nguyên tắc tạo ra các chuỗi dài của các phần tử dường như ngẫu nhiên và được giải mã bằng cách sử dụng một máy thu độc lập tạo ra cùng một chuỗi các phần tử.
Các thanh ghi dịch chuyển phản hồi tuyến tính đã được đánh giá cao trong mật mã do khoảng thời gian lặp lại dài của chúng. Tuy nhiên, phân tích toán học mà Saul sử dụng để tìm các khoảng thời gian này cho thấy rõ ràng rằng các thanh ghi dịch chuyển như vậy không phù hợp với mật mã an toàn. Tuy nhiên, lúc đầu chúng có vẻ khá ổn (đặc biệt là so với các vị trí liên tiếp của cánh quạt trong Enigma); Có tin đồn dai dẳng rằng các hệ thống mật mã quân sự của Liên Xô được xây dựng trên cơ sở này.
Trở lại năm 2001 khi tôi đang làm việc trên các ghi chép lịch sử cho cuốn sách của mình Một loại khoa học mới Tôi và Saul đã nói chuyện điện thoại rất lâu về ca đăng ký. Saul nói với tôi rằng khi anh ấy bắt đầu, anh ấy không biết gì về công việc mật mã trên sổ đăng ký ca làm việc. Anh ấy nói rằng Bell Labs, Lincoln Labs và Jet Propulsion Labs đã bắt đầu làm việc trên các sổ đăng ký ca làm việc cùng thời gian với anh ấy; tuy nhiên, ông đã cố gắng tiến xa hơn một chút, điều mà ông ghi nhận trong báo cáo năm 1955 của mình.
Trong những năm sau đó, Sau-lơ dần dần nhận thức được những tiền thân khác nhau của công trình nghiên cứu về toán học thuần túy của ông. Ngay từ năm 1202, Fibonacci đã nói về những gì ngày nay được gọi là số Fibonacci, được tạo ra bởi một quan hệ lặp lại (có thể được coi là tương tự như một thanh ghi dịch chuyển phản hồi tuyến tính hoạt động trên các số nguyên tùy ý thay vì 0 và 1). Cũng có những công trình nhỏ từ đầu những năm 1900 về chu kỳ 0 và 1, nhưng nghiên cứu quy mô lớn đầu tiên là của Øysten Ore tại Đại học Oslo. Ore có một sinh viên tên là Marshall Hall, người đã cố vấn cho tiền thân của Cơ quan An ninh Quốc gia vào cuối những năm 1940. - có thể là về chủ đề của sổ đăng ký thay đổi. Tuy nhiên, mọi thứ anh ấy làm đều được phân loại, và vì vậy anh ấy đã sắp xếp với Saul để xuất bản lịch sử của các thanh ghi dịch chuyển phản hồi tuyến tính; Saul đã dành tặng cuốn sách của mình cho Marshall Hall.
Trình tự được tạo bởi thanh ghi shift để làm gì?
Tôi đã quan sát nhiều lần rằng các hệ thống được xác định bởi các quy tắc đơn giản kết thúc với nhiều ứng dụng; thanh ghi dịch chuyển cũng tuân theo mô hình này. Cả phần cứng và phần mềm hiện đại đều được nhồi nhét với các thanh ghi dịch chuyển: một điện thoại di động điển hình có thể có một tá hoặc hai thanh ghi trong số chúng, thường được thực hiện trong phần cứng và đôi khi trong phần mềm (khi tôi viết "thanh ghi dịch chuyển" ở đây, ý tôi là thanh ghi dịch chuyển phản hồi tuyến tính - LFSR).Trong hầu hết các trường hợp, các thanh ghi dịch chuyển đó được sử dụng để cung cấp các chuỗi có độ dài tối đa (còn được gọi là " Trình tự M"). Lý do chúng được sử dụng có xu hướng là do một số tính chất của chúng, mà Sol đã phát hiện ra. Chúng luôn chứa cùng một số 0 và 1 (mặc dù trên thực tế luôn có chính xác thêm 1). Sau đó, Sol cho thấy rằng chúng cũng thường có cùng số chuỗi 00, 01, 10 và 11 - và đối với các khối lớn cũng vậy. Thuộc tính này " thăng bằng"Bản thân điều này đã rất hữu ích - ví dụ: nếu bạn kiểm tra tất cả các kết hợp có thể có của các bit làm đầu vào.
Tuy nhiên, Sol đã phát hiện ra một tài sản khác, thậm chí còn quan trọng hơn. Thay mỗi số 0 trong dãy bằng 1, sau đó nhân mỗi phần tử trong phiên bản dịch chuyển của dãy với phần tử tương ứng trong bản gốc. Sol chỉ ra rằng khi thêm vào, các phần tử này sẽ luôn bằng 0 (trừ trường hợp không có sự dịch chuyển nào cả). Đó là, trình tự không có mối tương quan với các phiên bản đã dịch chuyển của chính nó.
Các thuộc tính này sẽ đúng với bất kỳ chuỗi ngẫu nhiên đủ dài nào gồm các số 0 và 1. Đáng ngạc nhiên là đối với các chuỗi có độ dài tối đa, các đặc tính này luôn đúng. Các chuỗi có một số đặc điểm của tính ngẫu nhiên, nhưng chúng không thực sự ngẫu nhiên chút nào: chúng có một cấu trúc được xác định rõ ràng, có tổ chức.
Chính cấu trúc này vốn có trong các thanh ghi dịch chuyển phản hồi tuyến tính khiến chúng không phù hợp với mật mã nghiêm túc. Nhưng chúng rất tốt cho việc "sắp xếp lại các phần tử" cơ bản và mật mã rẻ tiền và được sử dụng tích cực cho những mục đích này. Thông thường, nhiệm vụ chỉ đơn giản là "làm trắng" tín hiệu (như trong "tiếng ồn trắng"). Đôi khi cần truyền dữ liệu với chuỗi dài bằng 0. Nhưng trong trường hợp này, thiết bị điện tử có thể bị nhầm lẫn nếu "khoảng lặng" quá lâu. Người ta có thể tránh vấn đề này bằng cách xáo trộn dữ liệu gốc bằng cách kết hợp nó với chuỗi được tạo bởi thanh ghi shift. Đây chính xác là những gì đã được thực hiện với Wi-Fi, Bluetooth, USB, TV kỹ thuật số, internet, v.v.
Một tác dụng phụ của việc xáo trộn thanh ghi dịch chuyển là giải mã phức tạp hơn, đôi khi được sử dụng để cải thiện bảo mật (công nghệ DVD sử dụng kết hợp thanh ghi dịch chuyển 16 và 24 bit để mã hóa dữ liệu; nhiều điện thoại GSM sử dụng kết hợp ba thanh ghi dịch chuyển để mã hóa tất cả các tín hiệu ).
Saul đã tạo ra nền tảng toán học cho tất cả, và cũng giới thiệu một số nhân vật quan trọng cho nhau. Ngay từ năm 1959, ông đã gặp Irvin Jacobs, người vừa nhận bằng Tiến sĩ tại Viện Công nghệ Massachusetts. Anh cũng biết Andy Viterbi, người làm việc tại Phòng thí nghiệm Sức đẩy Phản lực. Saul giới thiệu họ và vào năm 1968, họ thành lập một công ty tên là Linkabit, làm việc trên các hệ thống mã hóa (hầu hết cho mục đích quân sự).
Năm 1985, Jacobs và Viterbi thành lập một công ty khác có tên là Qualcomm. Lúc đầu, họ không hoạt động tốt lắm, nhưng đến đầu những năm 1990, khi họ bắt đầu chế tạo các thành phần để triển khai CDMA trong điện thoại di động, công ty bắt đầu phát triển nhanh chóng.
Chà, những thanh ghi này ở đâu?
Điều đáng ngạc nhiên là hầu hết mọi người chưa bao giờ nghe nói đến thanh ghi shift và chưa tương tác với chúng bất cứ khi nào họ sử dụng các hệ thống truyền thông hiện đại, máy tính, v.v. Rất dễ nhầm lẫn ở đây, vì cùng một chuỗi các thanh ghi nhưng lại có những tên khác nhau. và các từ viết tắt chuyển đổi phản hồi tuyến tính (chuỗi PN, PN, M-, FSR, LFSR, MLS, SRS, PRBS, v.v.).Nếu chúng ta xem xét điện thoại di động, thì việc sử dụng các chuỗi được tạo ra bởi các thanh ghi dịch chuyển trong chúng đã thay đổi trong những năm qua, tăng hoặc giảm. mạng dựa trên TDMA, vì vậy chúng không sử dụng trình tự do thanh ghi dịch chuyển tạo ra để mã hóa dữ liệu của mình, nhưng vẫn thường sử dụng CRC (mã dự phòng theo chu kỳ) để kiểm tra các khối dữ liệu. mạng là những người sử dụng CDMA lớn nhất, do đó, các trình tự được tạo ra bởi các thanh ghi dịch chuyển có liên quan đến việc truyền mỗi bit. mạng thường sử dụng kết hợp các khe thời gian và tần số không bao gồm trình tự thanh ghi dịch chuyển, mặc dù CRC vẫn được sử dụng: ví dụ: để xử lý dữ liệu nhất quán khi các cửa sổ tần số chồng lên nhau. có cấu trúc phức tạp hơn - với nhiều ăng ten tự động thích ứng để sử dụng thời gian và tần số khe cắm tối ưu. Tuy nhiên, một nửa số kênh của họ thường dành riêng cho tín hiệu "hoa tiêu", được sử dụng để suy ra môi trường vô tuyến cục bộ; chúng cũng dựa trên các trình tự được tạo ra bởi các thanh ghi dịch chuyển.
Trong sản xuất điện tử, mục tiêu thường là đạt được tốc độ dữ liệu cao nhất có thể với lượng điện năng ít nhất cần thiết để cho phép các bit vượt qua tầng nhiễu. Và, như một quy luật, đường dẫn này dẫn đến tự động hóa phát hiện lỗi, và do đó, sử dụng CRC (mã dự phòng theo chu kỳ) và do đó, các trình tự được tạo bởi thanh ghi dịch chuyển. Điều này áp dụng cho hầu hết các loại bus bên trong máy tính (PCIe, SATA, v.v.): cung cấp sự tương tác giữa các bộ phận của bộ xử lý trung tâm hoặc nhận dữ liệu từ các thiết bị hoặc kết nối với màn hình bằng HDMI. Trong trường hợp đĩa hoặc bộ nhớ, CRC và các mã khác dựa trên trình tự được tạo bởi thanh ghi dịch chuyển cũng hầu như được sử dụng phổ biến để hoạt động ở tốc độ tối đa.
Thanh ghi Shift rất phổ biến đến mức gần như không thể ước tính được chúng tạo ra bao nhiêu bit. Có khoảng 10 tỷ máy tính, ít điện thoại hơn một chút và một số lượng lớn thiết bị trong IoT được nhúng ("Internet of Things"). Hầu hết mọi chiếc ô tô trên thế giới (và có hơn một tỷ chiếc trong số đó!) Đều có khoảng 10 bộ vi xử lý được tích hợp sẵn.
Thanh ghi dịch chuyển hoạt động ở tần số nào? Hệ thống truyền thông có tần số sóng mang cơ bản trong dải hertz, cũng như "tốc độ chip", dùng để chỉ tốc độ đa truy nhập (chúng ta đang nói về CDMA) trong dải MHz. Mặt khác, trong các xe buýt bên trong máy tính, tất cả dữ liệu được truyền bằng cách sử dụng thanh ghi shift - với tốc độ truyền tốt nhất trong phạm vi hertz.
Có ít nhất 10 tỷ đường truyền thông chạy trong ít nhất 1/10 tỷ giây (khoảng 3 năm) sử dụng ít nhất 1 tỷ bit thanh ghi dịch chuyển mỗi giây, có nghĩa là thuật toán của Saul đã được sử dụng ít nhất một tỷ lần.
Thuật toán này có thực sự được sử dụng thường xuyên nhất không? Tôi nghĩ là có. Tôi nghi ngờ rằng chỉ có các phép toán số học mới có thể cạnh tranh được. Ngày nay, các bộ xử lý có khả năng thực hiện một nghìn tỷ phép tính số học mỗi giây và các hoạt động như vậy là bắt buộc đối với hầu hết mọi bit do máy tính tạo ra. Nhưng số học được thực hiện như thế nào? Ở một mức độ nào đó, nó chỉ là một triển khai của điện tử kỹ thuật số.
Tuy nhiên, có những "ý tưởng thuật toán" mà bất cứ ai ngoài các nhà thiết kế bộ vi xử lý vẫn không thể hiểu được. Khi Babbage đang tạo ra động cơ khác biệt của mình (xem bài báo của Habré "Làm sáng tỏ câu chuyện của Ada Lovelace (lập trình viên đầu tiên trong lịch sử)"), việc thực hiện đã trở thành một trở ngại lớn trong việc thực hiện các phép toán số học (trên thực tế, có thể nghĩ đến một thanh ghi dịch chuyển phản hồi tuyến tính giống như một hệ thống thực hiện một cái gì đó giống như số học, nhưng không thực hiện chuyển giao). Có "cây truyền tín hiệu chuyển giao" tối ưu hóa việc chuyển giao. Ngoài ra còn có một số thủ thuật nhỏ (như thuật toán Booth, cây Wallace, v.v.) làm giảm số lượng các phép toán bit cần thiết để tạo ra "ruột" của số học. Nhưng, không giống như các thanh ghi dịch chuyển phản hồi tuyến tính, đơn giản là không có ý tưởng thuật toán đơn lẻ nào có thể được sử dụng hầu như ở mọi nơi; vì vậy tôi nghĩ rằng các trình tự dài nhất được tạo ra bởi các thanh ghi dịch chuyển phản hồi tuyến tính vẫn giành chiến thắng trong số các trình tự được sử dụng nhiều nhất.
Dữ liệu tự động di động và thanh ghi dịch chuyển với phản hồi phi tuyến tính
Mặc dù thoạt nhìn có vẻ không rõ ràng, nhưng hóa ra có một mối quan hệ chặt chẽ giữa thanh ghi dịch chuyển phản hồi và dữ liệu tự động di động mà tôi đã nghiên cứu trong nhiều năm. Tổ chức cơ bản cho một thanh ghi dịch chuyển phản hồi là tính toán từng bit một. Một ô tự động hóa di động có một dòng ô và ở mỗi bước, tất cả các ô đều được cập nhật song song, dựa trên một quy tắc, ví dụ: phụ thuộc vào giá trị của các hàng xóm gần nhất của chúng.Để xem chúng có liên quan như thế nào, bạn cần chạy thanh ghi thay đổi phản hồi kích thước n và đồng thời hiển thị trạng thái của nó chỉ mỗi n các bước; nói cách khác, hãy để tất cả các bit được ghi đè trước khi chúng xuất hiện trở lại. Nếu mỗi bước của thanh ghi dịch chuyển phản hồi tuyến tính (ở đây có hai lần nhấn) được hiển thị, thì ở mỗi bước, mọi thứ sẽ chuyển sang trái - và thế là xong. Nhưng nếu bạn tạo ảnh nén, chỉ hiển thị mỗi n các bước, một mẫu sẽ trở nên hiển thị.

Đây là một mẫu lồng nhau; và hình ảnh này rất giống với hình ảnh có thể thu được nếu tự động hóa tế bào lấy một ô và hàng xóm của nó và thêm chúng mô-đun 2 (XOR). Đây là những gì sẽ xảy ra với một tự động hóa di động nếu nó sắp xếp các ô của nó để chúng nằm trong một vòng tròn có cùng kích thước với thanh ghi shift ở trên:

Ban đầu, dữ liệu tự động di động và các mẫu thanh ghi dịch chuyển hoàn toàn giống nhau. Nhìn vào những bức ảnh này, sẽ ít ngạc nhiên hơn rằng toán học của các thanh ghi dịch chuyển phải có liên quan đến dữ liệu tự động di động. Và với sự lặp lại của các mẫu lồng nhau, nó trở nên rõ ràng tại sao cần có một lý thuyết toán học thanh lịch về thanh ghi dịch chuyển.
Các thanh ghi dịch chuyển điển hình được sử dụng trong thực tế không có các mẫu lặp lại rõ ràng như vậy. Dưới đây là một số ví dụ về thanh ghi dịch chuyển tạo chuỗi có độ dài tối đa. Thực tế là các nhánh cây cách xa nhau nên khó tìm thấy dấu vết trực quan của việc làm tổ.

Mức độ tương ứng giữa thanh ghi dịch chuyển và dữ liệu tự động di động rộng như thế nào? Đối với dữ liệu tự động di động, các quy tắc để tạo giá trị ô mới có thể là bất cứ điều gì. Trong các thanh ghi dịch chuyển phản hồi tuyến tính, chúng phải luôn dựa trên phép cộng modulo 2 (hoặc XOR). Đây là phần "tuyến tính" của "thanh ghi dịch chuyển phản hồi tuyến tính" có nghĩa là. Cũng có thể sử dụng bất kỳ quy tắc nào để kết hợp các giá trị cho các thanh ghi dịch chuyển phản hồi phi tuyến tính (NFSR).
Thật vậy, khi Saul phát triển lý thuyết của mình cho các thanh ghi dịch chuyển phản hồi tuyến tính, ông bắt đầu với một trường hợp phi tuyến tính. Khi đến JPL vào năm 1956, ông nhận được một phòng thí nghiệm hoàn chỉnh với các giá đỡ cho các mô-đun điện tử nhỏ. Saul nói rằng các mô-đun (mỗi mô-đun có kích thước bằng một bao thuốc lá) được xây dựng cho dự án Bell Labs để thực hiện một hoạt động logic cụ thể (VÀ, HOẶC, KHÔNG, ...). Các mô-đun có thể được sử dụng cùng nhau để triển khai bất kỳ thanh ghi dịch chuyển phản hồi phi tuyến tính nào mong muốn, cung cấp khoảng một triệu bit mỗi giây (Saul nói với tôi rằng ai đó đã cố gắng làm điều tương tự với một máy tính đa năng và điều đó mất 1 giây khi sử dụng mô-đun phần cứng , yêu cầu 6 tuần làm việc trên máy tính lớn).
Khi Sol bắt đầu nghiên cứu các thanh ghi dịch chuyển phản hồi tuyến tính, khám phá chính đầu tiên của ông là các khoảng thời gian lặp lại của chúng. Và trong trường hợp phi tuyến tính, anh ấy hướng phần lớn nỗ lực của mình vào việc cố gắng hiểu điều tương tự. Ông đã thu thập tất cả các loại dữ liệu thí nghiệm. Anh ấy nói với tôi rằng anh ấy thậm chí đã thử nghiệm các chuỗi có độ dài 245, mất một năm. Anh ấy đã thực hiện một bản tóm tắt như trong hình dưới đây (lưu ý hình dung của các trình tự được hiển thị trên đường dạng sóng). Nhưng anh ta không bao giờ nghĩ ra được một số loại lý thuyết chung, mà anh ta có cho các thanh ghi dịch chuyển phản hồi tuyến tính.

Không có gì ngạc nhiên khi anh ấy không thể làm điều đó. Ngay từ những năm 1950, đã có những kết quả lý thuyết (chủ yếu dựa trên ý tưởng về tính toán phổ quát của Turing) về những chương trình về nguyên tắc có thể làm được điều này. Tôi không nghĩ rằng Saul hoặc bất kỳ ai khác đã từng nghĩ rằng các thanh ghi dịch chuyển phản hồi phi tuyến tính sẽ có các chức năng rất đơn giản (phi tuyến tính).
Và chỉ sau này, người ta mới biết rõ hành vi của các chương trình thậm chí rất đơn giản có thể phức tạp đến mức nào. Ví dụ yêu thích của tôi là quy tắc 30 cho ô tự động di động, trong đó giá trị của các ô lân cận được kết hợp bằng cách sử dụng một hàm có thể được biểu diễn dưới dạng R + q + r + q * r mod 2(hoặc là R Xor ( q HOẶC LÀ r)). Thật đáng kinh ngạc, Sol coi các thanh ghi dịch chuyển phản hồi phi tuyến tính dựa trên các chức năng tương tự: R + G + S + q * r + q * s + r * s mod 2. Dưới đây là hình ảnh minh họa về cách hàm Sol (có thể được coi là "quy tắc 29070"), quy tắc 30 và một vài quy tắc tương tự khác trong một thanh ghi dịch chuyển:

Và chúng đây, không giới hạn ở một thanh ghi có kích thước cố định, tương tự như dữ liệu tự động di động:

Tất nhiên Saul không bao giờ tạo ra những bức ảnh như thế này (và điều đó gần như không thể làm được vào những năm 1950). Thay vào đó, ông tập trung vào khoảng thời gian lặp lại như một loại đặc tính tích lũy.
Saul tự hỏi liệu các thanh ghi dịch chuyển phản hồi phi tuyến tính có thể là nguồn ngẫu nhiên hay không. Từ những gì hiện đã biết về tự động dữ liệu di động, rõ ràng là họ có thể làm được. Ví dụ, để tạo ra tính ngẫu nhiên trong Mathematica, chúng tôi đã sử dụng quy tắc 30 cellular automaton trong 25 năm (mặc dù gần đây chúng tôi đã bỏ nó để chuyển sang một quy tắc hiệu quả hơn mà chúng tôi đã tìm thấy sau khi khám phá hàng nghìn tỷ khả năng).
Saul không nói nhiều về mã hóa; mặc dù tôi nghĩ anh ấy đã không làm việc cho chính phủ lâu. Anh ấy nói với tôi rằng mặc dù vào năm 1959, anh ấy đã phát hiện ra " các cuộc tấn công tương quan đa biến trên các chuỗi phi tuyến tính", đồng thời anh ấy" cẩn thận tránh các tuyên bố rằng chương trình là để phân tích mật mã"Thực tế là quy tắc 30 cho tự động dữ liệu di động (và có lẽ cả thanh ghi dịch chuyển phản hồi phi tuyến tính) có thể là các hệ thống mật mã tốt - mặc dù do thực tế là chúng dường như tương đương với các thanh ghi dịch chuyển phản hồi tuyến tính (và điều này không phải như vậy), chúng không bao giờ được sử dụng nhiều nhất có thể.
Là một người đam mê, trong suốt vài thập kỷ qua, tôi đã cố gắng nghiên cứu tất cả các công trình tiền thân của công việc của mình về tự động hóa tế bào một chiều. Tự động hóa tế bào hai chiều còn ít được nghiên cứu, nhưng trong trường hợp tự động hóa một chiều, người ta chỉ tìm thấy một công trình thuần túy lý thuyết. Tôi nghĩ rằng các thanh ghi dịch chuyển phản hồi phi tuyến tính của Solomon Golomb là thứ gần nhất mà tôi từng thấy với những gì tôi đã làm trong một phần tư thế kỷ sau.
Poliomino
Nghe tên họ Golomb ", nhiều người sẽ nhớ các thanh ghi shift. Tuy nhiên, hầu hết sẽ nhớ về polyomino. Sau-lơ không phát minh ra polyomino, mặc dù ông đã nghĩ ra cái tên đó. Ông đã tạo ra một hệ thống những gì trước đây chỉ xuất hiện trong các câu đố riêng lẻ.Câu hỏi chính mà Sau-lơ muốn trả lời là làm cách nào để tổ chức các bộ polyomino để bao phủ một khu vực. Đôi khi nó khá rõ ràng và đôi khi nó khá khó khăn. Sol xuất bản bài báo đầu tiên của mình về polyominoes vào năm 1954, nhưng chính Martin Gardner mới là người làm cho polyominoes thực sự phổ biến vào năm 1957 (ông đã viết một chuyên mục về trò chơi toán học trên tạp chí Khoa học Mỹ). Như Sau-lơ đã giải thích trong lời tựa cho cuốn sách năm 1964 của mình, kết quả là " một lượng lớn phóng viên liên tục từ khắp nơi trên thế giới và từ mọi tầng lớp xã hội: chủ tịch hội đồng quản trị của các trường đại học hàng đầu, cư dân của các tu viện vô danh, tù nhân từ các nhà tù nổi tiếng ...".
Các công ty trò chơi cũng chú ý đến các câu đố mới và trong vòng vài tháng đã có những tiêu đề như " câu đố giật gân mới", tiếp theo là nhiều thập kỷ câu đố khác và các trò chơi dựa trên polyomino (không, gã trọc đầu nham hiểm trông không giống Saul):
Saul đã in các bài báo trên polyomino trong 50 năm nữa sau lần xuất bản đầu tiên. Năm 1961, ông đã giới thiệu "rep-tile", có thể được sử dụng để tạo các mẫu fractal ("infin-tile"). Nhưng hầu hết mọi thứ Sau-lơ làm với polyomino đều liên quan đến việc giải quyết các vấn đề cụ thể.
Tôi rất ít quan tâm đến tính đặc biệt của polyomino; Tôi quan tâm đến các hiện tượng tổng quát hơn liên quan đến chúng. Có vẻ như việc quyết định xem có thể "lát gạch" toàn bộ mặt phẳng bằng một vài hình khối đơn giản hay không là điều dễ dàng. Nhưng trong trường hợp của polyominoes (cũng như tất cả các trò chơi và câu đố dựa trên chúng), rõ ràng là mọi thứ không đơn giản như vậy. Thật vậy, vào những năm 1960, người ta đã chứng minh rằng vấn đề này về mặt lý thuyết là không thể giải được.
Nếu chúng ta chỉ quan tâm đến một khu vực hạn chế, thì về nguyên tắc, chúng ta có thể chỉ cần liệt kê tất cả các cách sắp xếp có thể hình dung được của các hình, và sau đó xem chúng có được đặt đúng vị trí hay không. Tuy nhiên, nếu chúng ta quan tâm đến vô cực, thì điều này không thể được thực hiện. Có thể ai đó sẽ tìm ra cách đặt thành công một triệu mảnh, nhưng không có gì đảm bảo rằng kết quả này có thể được kéo dài thêm.
Hóa ra nó có thể trông giống như một cỗ máy Turing đang chạy - hoặc một thiết bị tự động di động. Bạn bắt đầu với một dòng gạch. Sau đó, việc hỏi liệu có thể lát gạch vô hạn tương đương với việc hỏi liệu có thể thiết lập một máy Turing để duy trì hoạt động hay không. Vấn đề là nếu một máy Turing là phổ thông (nghĩa là nó có thể được lập trình để thực hiện bất kỳ phép tính nào có thể xảy ra), thì vấn đề tạm dừng đối với nó có thể không giải quyết được, có nghĩa là vấn đề lát gạch cũng sẽ không thể giải quyết được.
Tất nhiên, điều này phụ thuộc vào bộ định dạng ban đầu. Câu hỏi đặt ra là các hình dạng cần phức tạp như thế nào để mã hóa các phép tính phổ biến và dẫn đến một bài toán ốp lát không thể giải quyết được. Solomon Golomb nhận thức được tài liệu về chủ đề này, nhưng không đặc biệt quan tâm đến nó.
Các bộ polyominoes phức tạp và được thiết kế cẩn thận được biết là thực sự hỗ trợ tính toán phổ thông. Nhưng những gì về một bộ đơn giản? Nó có thực sự đơn giản đến mức tình cờ gặp phải không? Nếu bạn nhìn vào tất cả các hệ thống mà tôi đã nghiên cứu, bộ đơn giản nhất thực sự trở nên đơn giản. Tuy nhiên, rất khó để tìm thấy nó.
Một vấn đề đơn giản hơn nhiều là tìm polyominoes lấp đầy thành công các mặt phẳng, mặc dù chỉ không theo chu kỳ. Roger Penrose đã tìm thấy một ví dụ phù hợp vào năm 1994. Trong cuốn sách của tôi Một loại khoa học mới Tôi đã đưa ra một ví dụ đơn giản hơn một chút với 3 polyominoes:
Phần còn lại của câu chuyện
Saul ở tuổi 30 khi đạt được thành công đáng chú ý trong lĩnh vực máy ghi ca và polyominoes ... Anh ấy là một người rất năng động. Anh ấy đã viết vài trăm bài báo, một số là phần mở rộng của công việc trước đó của anh ấy, một số là câu trả lời cho những câu hỏi anh ấy được hỏi, và một số được viết chỉ để giải trí - để tìm hiểu những điều thú vị về các con số, chuỗi, hệ thống mật mã, v.v. d.Thanh ghi dịch chuyển và polyominoes là những chủ đề lớn (chúng thậm chí còn được phân loại trong phân loại AMS). Trong những thập kỷ gần đây, cả hai đều nhận được một bước phát triển mới, khi các thí nghiệm máy tính bắt đầu được thực hiện trên cơ sở của chúng; Sol cũng tham gia tích cực vào chúng. Tuy nhiên, nhiều câu hỏi vẫn chưa được giải đáp. Và nếu đối với thanh ghi dịch chuyển với phản hồi tuyến tính, bạn có thể tìm thấy ma trận Hadamard lớn, thì ngay cả bây giờ ít người biết về thanh ghi dịch chuyển với phản hồi phi tuyến, chưa kể đến tất cả các polyominoes không tuần hoàn và ngoại lai khác.
Saul luôn thích thú với các câu đố, cả toán học và câu đố chữ. Trong một thời gian, anh ấy đã viết một chuyên mục câu đố cho thời LA, và trong 32 năm đã viết " Golomb gambits cho tạp chí của cựu sinh viên Johns Hopkins. Anh ấy đã tham gia một bài kiểm tra MegaIQ và giành được một chuyến đi đến Nhà Trắng khi anh ấy và sếp của mình lọt vào top 5 người dẫn đầu cả nước.
Ông đã đầu tư rất nhiều nỗ lực cho công việc của mình tại trường đại học: không chỉ giảng dạy sinh viên và giám sát nghiên cứu sinh và leo lên bậc thang hành chính (chủ tịch hội đồng đại học, phó hiệu trưởng nghiên cứu, v.v.), mà còn bày tỏ quan điểm của mình về quản lý của trường đại học nói chung (ví dụ, đã viết một bài báo có tựa đề "Tư vấn của Khoa: Loại bỏ hay Giữ lại?"; Câu trả lời: không, điều đó tốt cho trường đại học!). Anh ấy là một thợ săn đầu người tại Đại học Nam California, và trong thời gian làm việc tại đây, anh ấy đã giúp trường đại học này vươn lên từ chỗ đứng đầu bảng xếp hạng giáo dục.
Và sau đó là tư vấn. Sau-lơ là người tỉ mỉ và không tiết lộ những gì mình đã làm cho các tổ chức chính phủ. Vào cuối những năm 1960, thất vọng vì tất cả mọi người trừ anh ấy đang bán trò chơi polyomino, Saul thành lập một công ty mà anh ấy gọi là Recreational Technology, Inc. Mọi thứ diễn ra không quá suôn sẻ, nhưng Saul đã gặp Alvin Berlekamp, một giáo sư Berkeley có niềm đam mê với lý thuyết mã hóa và câu đố. Sau đó, họ thành lập công ty Cyclotomics (để vinh danh các đa thức cyclotomic có dạng x n- 1), cuối cùng đã được bán cho Kodak với một khoản tiền nhỏ (Berlekamp cũng tạo ra một hệ thống giao dịch thuật toán, sau đó ông bán cho Jim Simons và trở thành điểm khởi đầu cho Renaissance Technologies, một trong những quỹ đầu cơ lớn nhất hiện nay).
Hơn 10.000 bằng sáng chế bằng cách nào đó liên quan đến công việc của Sau-lơ, nhưng riêng Sau-lơ chỉ nhận được một bằng sáng chế trên các hệ thống mật mã dựa trên chuẩn tinh - và tôi nghĩ rằng anh ấy đã làm rất ít để thương mại hóa công việc của mình.
Sol đã làm việc với Technion, Viện Công nghệ Israel, trong nhiều năm. Anh ấy nói về mình là " người Do Thái chính thống không tôn giáo", nhưng đồng thời đôi khi cũng dẫn dắt các cuộc hội thảo dành cho người mới bắt đầu về Sách Sáng thế, và cũng làm việc để giải mã các phần của Cuộn Biển Chết (bản thảo Qumran).
Saul và vợ đã đi du lịch rất nhiều nơi, nhưng "trung tâm thế giới" của Saul chắc chắn là văn phòng Los Angeles của anh ấy tại Đại học Nam California, và ngôi nhà mà anh ấy và vợ đã sống trong gần 60 năm. Anh luôn được bạn bè và học sinh vây quanh. Và anh ấy đã có một gia đình. Con gái của ông, Astrid đã đóng vai một học sinh trong vở kịch về Richard Feynman (cô ấy đóng thế cho anh ấy), và trong cuốn tiểu thuyết của bạn tôi là một trong những nhân vật. Beatrice đã cống hiến sự nghiệp của mình để áp dụng mức độ chính xác toán học vào các loại chỉ định và chẩn đoán y tế khác nhau (các bệnh liên quan đến Chiến tranh vùng Vịnh, hiệu ứng statin, nấc cụt, v.v.). Tôi thậm chí đã đóng góp một phần nhỏ cho cuộc đời của Beatrice bằng cách giới thiệu cô ấy với người đàn ông sẽ trở thành chồng cô ấy, Terry Sejnowski, một trong những người sáng lập ra khoa học thần kinh tính toán hiện đại.
Sol dường như có liên quan đến rất nhiều thứ, ngay cả khi anh ấy không đi vào quá nhiều chi tiết. Đôi khi, tôi muốn nói chuyện với anh ấy về khoa học và toán học, nhưng anh ấy lại thích kể những câu chuyện (thường rất thú vị) về cả cá nhân và tổ chức (" Bạn có thể tin rằng [vào năm 1985], sau khi vắng mặt trong các hội nghị trong nhiều năm, Claude Shannon chỉ xuất hiện không báo trước tại quầy bar tại hội nghị lý thuyết thông tin hàng năm?"; "Bạn có biết người đứng đầu Caltech đã phải trả bao nhiêu để đưa anh ta đến Ả Rập Xê Út không?", Vân vân.).
Khi nhìn lại, tôi nhận ra rằng tôi muốn Saul quan tâm đến việc giải quyết một số vấn đề toán học được nêu ra trong công việc của tôi. Tôi không nghĩ rằng mình đã từng nhận ra rằng anh ấy thích giải quyết những vấn đề mà người khác đề nghị đến nhường nào. Bất chấp những đóng góp đáng kể của mình đối với cơ sở hạ tầng của thế giới điện toán, bản thân Saul chưa bao giờ thực sự sử dụng máy tính. Anh rất tự hào về việc anh có thể dễ dàng thực hiện các phép tính trong đầu. Cho đến khi 70 tuổi, ông không sử dụng e-mail và không bao giờ sử dụng máy tính ở nhà, mặc dù ông có điện thoại di động (hầu như ông không bao giờ nhận được e-mail thường xuyên. Tôi đã từng đề cập rằng khoảng một năm trước, tôi đã nghiên cứu lịch sử của Ada Lovelace; anh ấy trả lời: " Câu chuyện về Ada Lovelace là lập trình viên của Babbage phổ biến đến mức mọi người dường như chấp nhận nó là sự thật, tuy nhiên tôi chưa bao giờ xem bất kỳ nguồn nào về chủ đề này.").
Các con gái của Sol đã tổ chức bữa tiệc sinh nhật lần thứ 80 của ông vài năm trước và tạo ra những lời mời thú vị sau:

Saul gặp một số vấn đề về sức khỏe, mặc dù điều này dường như không ảnh hưởng nhiều đến nhịp sống của anh. Sức khỏe của vợ anh ngày càng giảm sút, và trong vài tuần gần đây khá nghiêm trọng. Vào ngày thứ Sáu, Sau-lơ đến văn phòng của mình như thường lệ, và vào đêm thứ Bảy, anh ta chết trong giấc ngủ. Vợ anh Bo sống sót sau anh hai tuần và qua đời chỉ hai ngày trước lễ kỷ niệm 60 năm ngày cưới của họ.
Mặc dù Saul đã biến mất, công việc của anh ấy vẫn tồn tại trong hàng tỷ bit của thế giới kỹ thuật số.
Vĩnh biệt Sol. Và từ tất cả chúng tôi, cảm ơn bạn.
Trình tự thanh ghi dịch chuyển được sử dụng trong cả lý thuyết mật mã và mã hóa. Lý thuyết của họ đã được phát triển rất tốt, các mật mã dòng dựa trên thanh ghi dịch chuyển là nguồn gốc của mật mã quân sự từ rất lâu trước khi điện tử ra đời.
Thanh ghi dịch chuyển phản hồi (sau đây gọi là PgCsOS) bao gồm hai phần: thanh ghi dịch chuyển và chức năng phản hồi. Thanh ghi dịch chuyển là một chuỗi các bit. Số lượng bit được xác định độ dài thanh ghi dịch chuyển, nếu độ dài là n bit, thì thanh ghi được gọi là thanh ghi dịch chuyển n-bit. Bất cứ khi nào cần trích xuất một bit, tất cả các bit của thanh ghi dịch chuyển được dịch sang phải 1 vị trí. Bit ngoài cùng bên trái mới là một chức năng của tất cả các bit khác trong thanh ghi. Đầu ra của thanh ghi dịch chuyển là một, thường là bit ít quan trọng nhất. Thời gian đăng ký thay đổi là độ dài của chuỗi kết quả trước khi nó bắt đầu lặp lại.
Hình 1. Thanh ghi dịch chuyển phản hồi
Thanh ghi Shift nhanh chóng được sử dụng trong mật mã luồng, vì chúng được thực hiện dễ dàng bằng phần cứng kỹ thuật số. Năm 1965, Ernst Selmer, nhà mật mã học chính của chính phủ Na Uy, đã phát triển lý thuyết chuỗi thanh ghi dịch chuyển. Solomon Golomb, một nhà toán học của NSA, đã viết một cuốn sách trình bày một số kết quả của ông và của Selmer. Loại thanh ghi dịch chuyển phản hồi đơn giản nhất là thanh ghi dịch chuyển phản hồi tuyến tính (LFSR hoặc PrCsLOS). Phản hồi của các thanh ghi như vậy chỉ đơn giản là một XOR (phép cộng hai modulo) của một số bit của thanh ghi, danh sách các bit này được gọi là chuỗi vòi. Đôi khi một thanh ghi như vậy được gọi là cấu hình Fibonacci. Do sự đơn giản của chuỗi phản hồi, một lý thuyết toán học khá phát triển có thể được sử dụng để phân tích PgCsLOC. Bằng cách phân tích các chuỗi đầu ra kết quả, bạn có thể xác minh rằng các chuỗi này là ngẫu nhiên đủ để an toàn. Thanh ghi dịch chuyển được sử dụng thường xuyên hơn các thanh ghi dịch chuyển khác trong mật mã.

Hình 2
Nói chung, một PrCsLOS n bit có thể ở một trong N = 2 n -1 trạng thái bên trong. Điều này có nghĩa là về mặt lý thuyết một thanh ghi như vậy có thể tạo ra một chuỗi giả ngẫu nhiên với chu kỳ T = 2 n -1 bit. (Số lượng trạng thái bên trong và chu kỳ là N = T max = 2 n -1, bởi vì việc điền PrCsLOS bằng các số không sẽ khiến thanh ghi dịch chuyển xuất ra một dãy số không vô hạn, điều này hoàn toàn vô dụng). Chỉ với một số trình tự chạm nhất định, PrCsLOS sẽ quay vòng qua tất cả 2 n -1 trạng thái bên trong, PrCsLOS như vậy RgSsLOS với khoảng thời gian tối đa. Kết quả thu được được gọi là Dãy M.
Thí dụ . Hình dưới đây cho thấy một PrCsLOS 4 bit với một lần nhấn từ bit đầu tiên và thứ tư. Nếu nó được khởi tạo với giá trị 1111, thì trước khi lặp lại thanh ghi sẽ có các trạng thái bên trong sau:
 Chuyển số đánh dấu (trạng thái bên trong) |
Đăng ký trạng thái |
bit đầu ra |
|||
|
Giá trị ban đầu |
|||||
|
15 (trở về trạng thái ban đầu) |
|||||
|
16 (trạng thái lặp lại) |
Chuỗi đầu ra sẽ là một chuỗi các bit có ý nghĩa nhỏ nhất: 1 1 1 1 0 1 0 1 1 0 0 1 0 0 0 với chu kỳ T = 15, tổng số trạng thái bên trong có thể có (ngoại trừ 0), N = 2 4 -1 = 16-1 = 15 = T max, do đó, trình tự đầu ra là một chuỗi M.
Để một PrCcLOS cụ thể có chu kỳ lớn nhất, đa thức được hình thành từ dãy vòi và hằng số 1 phải là môđun nguyên thủy 2. Đa thức được biểu diễn dưới dạng tổng lũy thừa, ví dụ: đa thức bậc n được biểu diễn dưới dạng sau:
Một n xn + a n-1 x n-1 +… + a 1 x 1 + a 0 x 0 = a n xn + a n-1 x n-1 +… + a 1 x + a 0 , nơi một tôi = (0,1) với i = 1… n, a x i - cho biết chữ số.
Bậc của đa thức là độ dài của thanh ghi dịch chuyển. Đa thức nguyên hàm bậc n là một đa thức bất khả quy là ước của x 2n? 1 +1 nhưng không phải là ước của x d +1 với mọi d là ước của 2n -1. Lý thuyết toán học tương ứng có thể được tìm thấy trong.
Nói chung, không có cách nào dễ dàng để tạo ra đa thức nguyên thủy có mô đun bậc 2. Cách dễ nhất là chọn ngẫu nhiên một đa thức và kiểm tra xem nó có phải là đa thức nguyên thủy hay không. Điều này không dễ dàng và phần nào giống như việc kiểm tra xem một số được chọn ngẫu nhiên có phải là số nguyên tố hay không - nhưng nhiều gói phần mềm toán học có thể giải quyết vấn đề này.
Một số, nhưng chắc chắn không phải là tất cả, đa thức ở các bậc khác nhau, modulo nguyên thủy 2, được đưa ra dưới đây. Ví dụ, mục nhập
(32, 7, 5, 3, 2, 1, 0) có nghĩa là đa thức sau là nguyên hàm modulo 2: x 32 + x 7 + x 5 + x 3 + x 2 + x + 1.
Điều này có thể dễ dàng khái quát thành PrCcLOC với khoảng thời gian tối đa. Số đầu tiên là độ dài của PrCsLOS. Số cuối cùng luôn là 0 và có thể được bỏ qua. Tất cả các số ngoại trừ số 0 chỉ định một chuỗi chạm, được tính từ cạnh trái của thanh ghi dịch chuyển. Nghĩa là, các số hạng của đa thức có bậc thấp hơn tương ứng với các vị trí gần mép phải của thanh ghi hơn.
Tiếp tục ví dụ, viết (32, 7, 5, 3, 2, 1, 0) có nghĩa là đối với một thanh ghi dịch chuyển 32 bit nhất định, một bit mới được tạo ra bằng cách XORing thứ ba mươi hai, thứ bảy, thứ năm, thứ ba, thứ hai và các bit đầu tiên, RgCsLOS kết quả sẽ có độ dài tối đa, lặp lại 2 giá trị 32 -1.

Hình 4. PrCsLOS 32-bit với độ dài tối đa
Hãy xem xét mã chương trình PgCsLOS, trong đó chuỗi vòi được đặc trưng bởi đa thức (32, 7, 5, 3, 2, 1, 0). Trong ngôn ngữ C, nó trông như thế này:
static unsigned long ShiftRegister = 1;
/ * Mọi thứ trừ 0. * /
ShiftRegister = (((((ShiftRegister >> 31)
^ (ShiftRegister >> 6)
^ (ShiftRegister >> 4)
^ (ShiftRegister >> 2)
^ (ShiftRegister >> 1)
^ ShiftRegister))
| (ShiftRegister >> 1);
trả về ShiftRegister & 0x00000001;)
Nếu thanh ghi shift dài hơn một từ máy tính, mã sẽ trở nên phức tạp hơn, nhưng không nhiều. Phụ lục B chứa bảng một số đa thức nguyên thủy modulo 2, chúng tôi sẽ sử dụng bảng này trong tương lai để xác định một số thuộc tính của các đa thức này, cũng như trong việc triển khai phần mềm để thiết lập một chuỗi chạm.
Cần lưu ý rằng tất cả các phần tử của bảng đều có số lượng hệ số là số lẻ. Một bảng dài như vậy được cung cấp để làm việc thêm với PrCcLOC, vì PrCcLOC thường được sử dụng cho mật mã với mật mã dòng và trong trình tạo số giả ngẫu nhiên. Trong trường hợp của chúng ta, chúng ta có thể sử dụng đa thức với bậc cao nhất không quá bảy.
Nếu p (x) là nguyên hàm, thì x n p (1 / x) cũng vậy, do đó mỗi phần tử của bảng thực sự xác định hai đa thức nguyên thủy. Ví dụ, nếu (a, b, 0) là nguyên thủy, thì (a, a-b, 0) cũng vậy. Nếu (a, b, c, d, 0) là nguyên thủy thì (a, a-d, a-c, a-b, 0) cũng vậy. Về mặt toán học:
nếu x a + x b +1 là nguyên thủy thì x a + x a-b +1 cũng vậy,
nếu x a + x b + x c + x d +1 là nguyên hàm thì x a + x a-d + x a-c + x a-b +1 cũng vậy. Các tam thức nguyên thủy nhanh nhất để triển khai theo chương trình, vì để tạo một bit mới, bạn chỉ cần XOR hai bit của thanh ghi shift (số hạng 0 không được tính đến, tức là x 0 \ u003d 1, xem ví dụ ở trên). Thật vậy, tất cả các đa thức phản hồi được đưa ra trong bảng là thưa thớt, tức là chúng có ít hệ số. Sự thưa thớt luôn là một điểm yếu, mà đôi khi đủ để mở thuật toán. Đối với các thuật toán mật mã, tốt hơn nhiều là sử dụng các đa thức nguyên thủy dày đặc, những đa thức có nhiều hệ số. Bằng cách sử dụng các đa thức dày đặc, đặc biệt là một phần của khóa, người ta có thể sử dụng PrCcLOC ngắn hơn nhiều.
Việc tạo ra các đa thức nguyên thủy dày đặc modulo 2 không phải là dễ dàng. Nói chung, để tạo ra các đa thức nguyên thủy bậc k, bạn cần phải biết nhân tử của số 2 k -1.
Tự bản thân, PgCsLOS là trình tạo chuỗi giả ngẫu nhiên tốt, nhưng chúng có một số đặc tính không ngẫu nhiên (xác định) không mong muốn. Các bit tuần tự là tuyến tính, làm cho chúng trở nên vô dụng cho việc mã hóa. Đối với PgCsLOS có độ dài n, trạng thái bên trong là n bit đầu ra trước đó của bộ tạo. Ngay cả khi sơ đồ phản hồi được giữ bí mật, nó có thể được xác định từ 2n bit đầu ra của bộ tạo bằng cách sử dụng thuật toán Berlekamp-Massey hiệu quả cao.
Ngoài ra, các số ngẫu nhiên lớn được tạo ra bằng cách sử dụng các bit liên tiếp của chuỗi này có tương quan cao và đối với một số loại ứng dụng, hoàn toàn không phải là ngẫu nhiên. Mặc dù vậy, PrCsLOS thường được sử dụng để tạo các thuật toán mã hóa như các thành phần của hệ thống và thuật toán mã hóa.
Đăng ký ca phản hồi bao gồm hai phần: thanh ghi ca và chức năng phản hồi.
Hình 19. Thanh ghi dịch chuyển phản hồi.
Nói chung, thanh ghi dịch chuyển là một chuỗi gồm một số phần tử của một vòng hoặc một trường. Được sử dụng phổ biến nhất chút các thanh ghi dịch chuyển. Chiều dài của một thanh ghi như vậy được biểu thị bằng một số bit. Mỗi khi một bit được truy xuất, tất cả các bit trong thanh ghi được dịch chuyển sang phải một vị trí. Bit quan trọng nhất mới được tính như một hàm của tất cả các bit khác trong thanh ghi. Đầu ra thường là bit ít quan trọng nhất. Khoảng thời gian của thanh ghi dịch chuyển là độ dài của chuỗi đầu ra trước khi nó bắt đầu lặp lại.
Loại thanh ghi dịch đơn giản nhất là thanh ghi dịch chuyển phản hồi tuyến tính (LFSR hoặc LRS). Phản hồi là một hoạt động XOR đơn giản trên một số bit của thanh ghi. Danh sách các bit này được xác định Đặc biệt đa thức và được gọi chạm vào trình tự. Đôi khi, lược đồ này được gọi là Cấu hình Fibonacci.

Hình 20. LFOS của cấu hình Fibonacci.
Trong phần mềm triển khai LFSR, một sơ đồ đã sửa đổi được sử dụng: để tạo ra một bit quan trọng mới, thay vì sử dụng các bit của chuỗi chạm, một thao tác XOR được thực hiện trên mỗi bit của nó với đầu ra của bộ tạo, thay thế cho các bit cũ bit của chuỗi vòi. Sửa đổi này đôi khi được gọi là Cấu hình Galois.

Hình 21. RLOS của cấu hình Galois.
n-bit LFSR có thể ở một trong 2 n- 1 trạng thái bên trong. Điều này có nghĩa là, về mặt lý thuyết, một thanh ghi như vậy có thể tạo ra một chuỗi giả ngẫu nhiên với chu kỳ là 2 n- 1 bit (đệm bằng số không hoàn toàn vô dụng). Thông hành của cả 2 n- 1 trạng thái bên trong chỉ có thể với một số trình tự vòi nhất định. Các thanh ghi như vậy được gọi là LFSR với khoảng thời gian tối đa. Để đảm bảo khoảng thời gian tối đa của LFSR, cần đa thức đặc trưng của nó là nguyên thủy modulo 2. Bậc của đa thức là độ dài của thanh ghi dịch chuyển. Đa thức bậc nguyên thủy n- Nó là như vậy không thể học được một đa thức là một ước nhưng không phải là một ước x d+1 cho tất cả d, là ước của 2 n- 1. (Khi thảo luận về đa thức, thuật ngữ số nguyên tốđược thay thế bởi thuật ngữ đa thức bất khả quy). Đa thức đặc trưng của LFSR được hiển thị trong các hình:
x 32 + x 7 + x 5 + x 3 + x 2 + x + 1
là modulo nguyên thủy 2. Khoảng thời gian của một thanh ghi như vậy sẽ là cực đại, đi qua tất cả 2 giá trị 32 - 1 cho đến khi chúng lặp lại. Thường được sử dụng nhất là các đa thức thu nhỏ, tức là chỉ có một số hệ số. các tam thức phổ biến nhất.
Một tham số quan trọng của trình tạo dựa trên LFSR là độ phức tạp tuyến tính. Nó được định nghĩa là chiều dài n LFSR ngắn nhất có thể mô phỏng đầu ra của bộ tạo. Độ phức tạp tuyến tính rất quan trọng vì với một Thuật toán Berlenkamp-Massey có thể tạo lại một LFSR như vậy bằng cách chỉ kiểm tra 2 n các bit gamma. Với định nghĩa của LFSR mong muốn, mật mã luồng thực sự đã bị hỏng.
Ngoài LFSR, các thanh ghi dịch chuyển với phản hồi phi tuyến tính, phản hồi chuyển giao, v.v. cũng được sử dụng.
Một số bộ tạo đã được phát triển dựa trên phương pháp lý thuyết số (bộ tạo Blum-Micali, RSA, BBS, bộ tạo nén, bộ tạo phụ gia, v.v.).
Hỗ trợ toán học cho việc tổng hợp các thuật toán mật mã dòng đã được phát triển đầy đủ và chi tiết hơn so với các thuật toán mật mã khối. Tuy nhiên, để tạo mật mã dòng, các thuật toán mật mã khối trong chế độ OFB hoặc CFB thường được sử dụng.

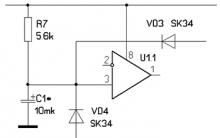
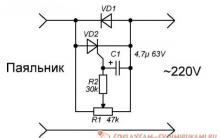






Pin không sạc
Các chương trình điều hướng tốt nhất: đánh giá các giải pháp cho thiết bị định vị GPS
Cách đặt ngày và giờ trên máy tính của bạn theo hai cách dễ dàng
Bật dịch vụ Windows Installer ở chế độ an toàn Cách bật gỡ cài đặt chương trình ở chế độ an toàn
Trình lưu trữ mặc định. Tạo kho lưu trữ ZIP. Cách hoạt động của winrar