tanım 1
Belirli bir doğru parçasında tanımlanan belirli bir $y=f(x)$ fonksiyonunun tüm ters türevlerinin kümesine verilen $y=f(x)$ fonksiyonunun belirsiz integrali denir. Belirsiz integral $\int f(x)dx $ sembolü ile gösterilir.
Yorum
Tanım 2 aşağıdaki gibi yazılabilir:
\[\int f(x)dx =F(x)+C.\]
Her irrasyonel fonksiyon, integrali temel fonksiyonlar cinsinden ifade edemez. Bununla birlikte, bu integrallerin çoğu, temel fonksiyonlar cinsinden ifade edilebilen rasyonel fonksiyonların integrallerine ikamelerle indirgenebilir.
$\int R\left(x,x^(m/n) ,...,x^(r/s) \sağ)dx $;
$\int R\left(x,\left(\frac(ax+b)(cx+d) \right)^(m/n) ,...,\left(\frac(ax+b)(cx +d) \sağ)^(r/s) \sağ)dx $;
$\int R\left(x,\sqrt(ax^(2) +bx+c) \right)dx $.
ben
$\int R\left(x,x^(m/n) ,...,x^(r/s) \right)dx $ biçiminde bir integral bulunurken, aşağıdaki yerine koyma yapılmalıdır:
Bu ikameyle, $x$ değişkeninin her bir kesirli kuvveti, $t$ değişkeninin tamsayı kuvveti cinsinden ifade edilir. Sonuç olarak, integral, $t$ değişkeninin rasyonel bir fonksiyonuna dönüşür.
örnek 1
Entegrasyon gerçekleştirin:
\[\int \frac(x^(1/2) dx)(x^(3/4) +1) .\]
Çözüm:
$k=4$, $\frac(1)(2) ,\, \, \frac(3)(4) $ kesirlerinin ortak paydasıdır.
\ \[\begin(dizi)(l) (\int \frac(x^(1/2) dx)(x^(3/4) +1) =4\int \frac(t^(2) ) (t^(3) +1) \cdot t^(3) dt =4\int \frac(t^(5) )(t^(3) +1) dt =4\int \left(t^( 2) -\frac(t^(2) )(t^(3) +1) \right)dt =4\int t^(2) dt -4\int \frac(t^(2) )(t ^(3) +1) dt =\frac(4)(3) \cdot t^(3) -) \\ (-\frac(4)(3) \cdot \ln |t^(3) +1 |+C) \end(dizi)\]
\[\int \frac(x^(1/2) dx)(x^(3/4) +1) =\frac(4)(3) \cdot \left+C\]
III
$\int R\left(x,\left(\frac(ax+b)(cx+d) \right)^(m/n) ,...,\left(\frac) formunun bir integralini bulurken (ax+ b)(cx+d) \right)^(r/s) \right)dx $ aşağıdaki değiştirmeyi yapmanız gerekir:
$k$, $\frac(m)(n) ,...,\frac(r)(s) $ kesirlerinin ortak paydasıdır.
Bu ikamenin bir sonucu olarak, integral, $t$ değişkeninin rasyonel bir fonksiyonuna dönüştürülür.
Örnek 2
Entegrasyon gerçekleştirin:
\[\int \frac(\sqrt(x+4) )(x) dx .\]
Çözüm:
Aşağıdaki ikameyi yapalım:
\ \[\int \frac(\sqrt(x+4) )(x) dx =\int \frac(t^(2) )(t^(2) -4) dt =2\int \left(1 +\frac(4)(t^(2) -4) \sağ)dt =2\int dt +8\int \frac(dt)(t^(2) -4) =2t+2\ln \left |\frac(t-2)(t+2) \sağ|+C\]
Ters ikame yaparak nihai sonucu elde ederiz:
\[\int \frac(\sqrt(x+4) )(x) dx =2\sqrt(x+4) +2\ln \left|\frac(\sqrt(x+4) -2)(\ sqrt(x+4) +2) \sağ|+C.\]
III
$\int R\left(x,\sqrt(ax^(2) +bx+c) \right)dx $ biçiminde bir integral bulunduğunda, sözde Euler ikamesi gerçekleştirilir (üç olası ikameden biri kullanıldı).
Euler'in ilk oyuncu değişikliği
$a> durumu için
$\sqrt(a) $'dan önce "+" işareti alarak şunu elde ederiz:
Örnek 3
Entegrasyon gerçekleştirin:
\[\int \frac(dx)(\sqrt(x^(2) +c) ) .\]
Çözüm:
Aşağıdaki ikameyi yapalım (durum $a=1>0$):
\[\sqrt(x^(2) +c) =-x+t,\, \, x=\frac(t^(2) -c)(2t) ,\, \, dx=\frac(t ^(2) +c)(2t^(2) ) dt,\, \, \sqrt(x^(2) +c) =-\frac(t^(2) -c)(2t) +t= \frac(t^(2) +c)(2t) .\] \[\int \frac(dx)(\sqrt(x^(2) +c) ) =\int \frac(\frac(t^ (2) +c)(2t^(2) ) dt)(\frac(t^(2) +c)(2t) ) =\int \frac(dt)(t) =\ln |t|+C \]
Ters ikame yaparak nihai sonucu elde ederiz:
\[\int \frac(dx)(\sqrt(x^(2) +c) ) =\ln |\sqrt(x^(2) +c) +x|+C.\]
Euler'in ikinci oyuncu değişikliği
$c>0$ durumu için aşağıdaki ikamenin yapılması gerekir:
$\sqrt(c) $'dan önce "+" işareti alarak şunu elde ederiz:
Örnek 4
Entegrasyon gerçekleştirin:
\[\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x+x^(2) ) ) dx .\]
Çözüm:
Aşağıdaki ikameyi yapalım:
\[\sqrt(1+x+x^(2) ) =xt+1.\]
\ \[\sqrt(1+x+x^(2) ) =xt+1=\frac(t^(2) -t+1)(1-t^(2) ) \] \
$\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x+x^(2) ) ) dx = \int \frac((-2t^(2) +t)^(2) (1-t)^(2) (1-t^(2))(2t^(2) -2t+2))( (1-t^(2))^(2) (2t-1)^(2) (t^(2) -t+1)(1-t^(2))^(2) ) dt =\ int \frac(t^(2) )(1-t^(2) ) dt =-2t+\ln \left|\frac(1+t)(1-t) \right|+C$ finali elde ederiz sonuç:
\[\begin(dizi)(l) (\int \frac((1-\sqrt(1+x+x^(2) ))^(2) )(x^(2) \sqrt(1+x) +x^(2) ) ) dx =-2\cdot \frac(\sqrt(1+x+x^(2) ) -1)(x) +\ln \left|\frac(x+\sqrt(1) +x+x^(2) ) -1)(x-\sqrt(1+x+x^(2) ) +1) \right|+C=-2\cdot \frac(\sqrt(1+x) +x^(2) ) -1)(x) +) \\ (+\ln \left|2x+2\sqrt(1+x+x^(2) ) +1\right|+C) \end (dizi)\]
Euler'in üçüncü oyuncu değişikliği
Daha önce, çeşitli formüller ve kurallar tarafından yönlendirilen belirli bir işlev için onun türevini bulmuştuk. Türevin çok sayıda uygulaması vardır: hareketin hızıdır (veya daha genel olarak herhangi bir sürecin hızı); fonksiyonun grafiğine teğetin eğimi; türevi kullanarak, monotonluk ve ekstremum fonksiyonunu inceleyebilirsiniz; Optimizasyon problemlerini çözmeye yardımcı olur.
Ancak bilinen bir hareket kanunundan hızı bulma probleminin yanı sıra, bir ters problem de vardır - hareket kanununu bilinen bir hızdan geri getirme problemi. Bu sorunlardan birini ele alalım.
örnek 1 Bir malzeme noktası düz bir çizgi boyunca hareket eder, t zamanındaki hareket hızı v=gt formülü ile verilir. Hareket yasasını bulun.
Çözüm. İstenen hareket yasası s = s(t) olsun. s"(t) = v(t) olduğu bilinmektedir. Bu nedenle, sorunu çözmek için, türevi gt'ye eşit olan bir s = s(t) fonksiyonu seçmeniz gerekir. Tahmin etmek kolaydır ki \( s(t) = \frac(gt^ 2)(2) \) Gerçekten
\(s"(t) = \left(\frac(gt^2)(2) \sağ)" = \frac(g)(2)(t^2)" = \frac(g)(2) \ cdot 2t=gt\)
Cevap: \(s(t) = \frac(gt^2)(2) \)
Hemen, örneğin doğru, ancak eksik çözüldüğünü not ediyoruz. \(s(t) = \frac(gt^2)(2) \ elde ettik. Aslında, sorunun sonsuz sayıda çözümü vardır: C'nin keyfi bir sabit olduğu \(s(t) = \frac(gt^2)(2) + C \) biçimindeki herhangi bir işlev, hareket, çünkü \(\left (\frac(gt^2)(2) +C \right)" = gt \)
Problemi daha spesifik hale getirmek için, başlangıç durumunu düzeltmemiz gerekiyordu: zamanın herhangi bir noktasında, örneğin t = 0'da hareket eden noktanın koordinatını belirtin. Diyelim ki, s(0) = s 0 , o zaman s(t) = (gt 2)/2 + C eşitliğini elde ederiz: s(0) = 0 + C, yani C = s 0 . Artık hareket yasası benzersiz bir şekilde tanımlanmıştır: s(t) = (gt 2)/2 + s 0 .
Matematikte karşılıklı ters işlemlere farklı adlar verilir, özel notasyonlar bulunur, örneğin: kare alma (x 2) ve karekök (\(\sqrt(x) \)) sinüs (sin x) ve arcsine ( arcsin x) vb. Verilen bir fonksiyona göre türevi bulma işlemine denir. farklılaşma ve ters işlem, yani belirli bir türev ile bir fonksiyon bulma süreci, - entegrasyon.
"Türev" teriminin kendisi "dünyevi bir şekilde" haklı çıkarılabilir: y \u003d f (x) işlevi "dünyaya" yeni bir y" \u003d f "(x) işlevi üretir. Y \u003d f (x) işlevi bir "ebeveyn" gibi davranır, ancak matematikçiler elbette ona "ebeveyn" veya "üretici" demezler, bunun y işleviyle ilgili olduğunu söylerler " = f" (x) , birincil görüntü veya ters türev.
Tanım.\(x \in X \) F"(x) = f(x) eşitliğini sağlıyorsa, y = F(x) işlevine X aralığındaki y = f(x) işlevi için ters türev denir
Uygulamada, X aralığı genellikle belirtilmez, ancak ima edilir (fonksiyonun doğal alanı olarak).
Örnekler verelim.
1) y \u003d x 2 işlevi, y \u003d 2x işlevi için bir ters türevdir, çünkü herhangi bir x için eşitlik (x 2) "\u003d 2x doğrudur
2) y \u003d x 3 işlevi, y \u003d 3x 2 işlevi için bir ters türevdir, çünkü herhangi bir x için eşitlik (x 3)" \u003d 3x 2 doğrudur
3) y \u003d sin (x) işlevi, y \u003d cos (x) işlevi için bir ters türevdir, çünkü herhangi bir x için eşitlik (sin (x)) "= cos (x) doğrudur
Ters türevleri ve türevleri bulurken, sadece formüller değil, aynı zamanda bazı kurallar da kullanılır. Türevleri hesaplamak için ilgili kurallarla doğrudan ilişkilidirler.
Bir toplamın türevinin, türevlerin toplamına eşit olduğunu biliyoruz. Bu kural, ters türevleri bulmak için karşılık gelen kuralı oluşturur.
Kural 1 Bir toplamın ters türevi, ters türevlerin toplamına eşittir.
Sabit çarpanın türevin işaretinden çıkarılabileceğini biliyoruz. Bu kural, ters türevleri bulmak için karşılık gelen kuralı üretir.
Kural 2 F(x), f(x) için bir ters türev ise, o zaman kF(x), kf(x) için bir terstürevdir.
teorem 1. Eğer y = F(x), y = f(x) fonksiyonunun ters türeviyse, o zaman y = f(kx + m) fonksiyonunun terstürevi \(y=\frac(1)(k)F fonksiyonudur) (kx+m) \)
Teorem 2. Eğer y = F(x), X aralığındaki bir y = f(x) fonksiyonu için bir ters türev ise, o zaman y = f(x) fonksiyonunun sonsuz sayıda ters türevi vardır ve bunların tümü y = F(x) biçimine sahiptir. + C.
Entegrasyon yöntemleri
Değişken değiştirme yöntemi (ikame yöntemi)
İkame entegrasyon yöntemi, yeni bir entegrasyon değişkeninin (yani, bir ikamenin) tanıtılmasından oluşur. Bu durumda, verilen integral, tablo şeklindeki veya ona indirgenebilen yeni bir integrale indirgenir. İkamelerin seçilmesi için genel bir yöntem yoktur. İkameyi doğru bir şekilde belirleme yeteneği uygulama ile kazanılır.
\(\textstyle \int F(x)dx \) integralini hesaplamak istensin. \(\varphi(t) \)'nin sürekli türevi olan bir fonksiyon olduğu bir \(x= \varphi(t) \) ikamesi yapalım.
Sonra \(dx = \varphi " (t) \cdot dt \) ve belirsiz integral integral formülünün değişmezlik özelliğine dayanarak, ikame integral formülünü elde ederiz:
\(\int F(x) dx = \int F(\varphi(t)) \cdot \varphi " (t) dt \)
\(\textstyle \int \sin^n x \cos^m x dx \) gibi ifadelerin entegrasyonu
Eğer m tek ise, m > 0, o zaman sin x = t ikamesini yapmak daha uygundur.
n tek ise, n > 0, cos x = t yerine koyma yapmak daha uygundur.
Eğer n ve m çift ise, o zaman tg x = t ikamesini yapmak daha uygundur.
Parçalara göre entegrasyon
Parçalara göre entegrasyon - entegrasyon için aşağıdaki formülün uygulanması:
\(\textstyle \int u \cdot dv = u \cdot v - \int v \cdot du \)
veya:
\(\textstyle \int u \cdot v" \cdot dx = u \cdot v - \int v \cdot u" \cdot dx \)
Bazı fonksiyonların belirsiz integralleri (ters türevler) tablosu
$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2) ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch) )x+C $$Matematik fakülteleri 1. ve 2. ders öğrencileri için testten fonksiyonların entegrasyonu ile ilgili hazır cevaplar alınır. Görevler ve cevaplardaki formüller görevlerin koşullarını tekrarlamasın diye yazmayacağız. Görevlerde "integrali bul" veya "integrali hesapla" yapmanız gerektiğini zaten biliyorsunuz. Bu nedenle, entegrasyonla ilgili yanıtlara ihtiyacınız varsa, aşağıdaki örnekleri incelemeye başlayın.
İrrasyonel fonksiyonların entegrasyonu
Örnek 18. İntegral altında bir değişken değişimi gerçekleştiriyoruz. Yeni değişken için hesaplamaları basitleştirmek için sadece kökü değil, paydanın tamamını seçiyoruz. Böyle bir değiştirmeden sonra, integral, basitleştirilmesi gerekmeyen iki tablo şeklindeki integralin toplamına dönüştürülür.
Entegrasyondan sonra, değişkenin yerine bir ikame koyarız.
Örnek 19. Bu kesirli irrasyonel işlevi entegre etmek için çok fazla zaman ve alan harcandı ve bir tabletten veya telefondan bir şeyi ayrıştırıp ayrıştıramayacağınızı bile bilmiyoruz. İrrasyonaliteden kurtulmak için ve burada yeni bir değişken için bir kübik kök ile uğraşıyoruz, kök fonksiyonunu üçüncü dereceye kadar seçiyoruz. Sonra diferansiyeli buluruz ve önceki fonksiyonu integralin altına alırız. 
Üstel bağımlılıklar ve kesirler için yeni fonksiyonun programı en çok zaman alır 
Dönüşümlerden sonra integrallerin bir kısmını hemen buluyoruz ve sonuncusunu tablo halindeki entegrasyon formüllerine göre dönüştürdüğümüz ikiye yazıyoruz. 
Tüm hesaplamalardan sonra, başlangıçta yapılan değiştirme işlemine geri dönmeyi unutmayın. 
Trigonometrik fonksiyonların entegrasyonu
Örnek 20. Sinüsün 7. dereceye kadar olan integralini bulmanız gerekiyor. Kurallara göre, diferansiyele bir sinüs sürülmelidir (kosinüs diferansiyelini elde ederiz) ve sinüsün 6. kuvveti kosinüs aracılığıyla yazılmalıdır. Böylece yeni değişken t = cos (x)'in fonksiyonundan integrasyona geliyoruz. Bu durumda, farkı küpe getirmeniz ve ardından entegre etmeniz gerekecektir. 


Sonuç olarak, kosinüsten 7. dereceden bir polinom elde ederiz.
Örnek 21. Bu integralde trigonometrik formüller için 4.derecenin kosinüsünü birinci dereceden kosinüs bağımlılığından yazmak gerekmektedir. Ardından, tablo şeklindeki kosinüs entegrasyon formülünü uyguluyoruz. 

Örnek 22. İntegralin altında sinüs ve kosinüsün çarpımı var. Trigonometrik formüllere göre sinüs farkından ürünü boyarız. Bu yayın nasıl elde edildiği "x"teki katsayıların analizinden anlaşılmaktadır. Sonra, sinüsleri entegre ediyoruz 
Örnek 23. Burada paydada hem sinüs hem de kosinüs fonksiyonumuz var. Ayrıca, trigonometrik formüller bağımlılığı basitleştirmeye yardımcı olmayacaktır. İntegrali bulmak için evrensel trigonometrik değişimi t=tan(x/2) uygularız.

Paydaların azalacağı ve kesrin paydasında bir kare üç terimli elde edeceğimiz kayıttan görülebilir. İçinde tam kareyi ve serbest kısmı seçiyoruz. Entegrasyondan sonra, paydanın basit çarpanları arasındaki farkın logaritmasına ulaşıyoruz. Gösterimi basitleştirmek için, logaritmanın altında hem pay hem de payda iki ile çarpıldı. 
Hesaplamaların sonunda bir değişken yerine argümanın yarısının tanjantını yerine koyuyoruz.
Örnek 24. Fonksiyonu entegre etmek için, kotanjantı bulmak için kosinüsün karesini köşeli parantezden alıp parantez içinde bir çıkarır ve ekleriz. 
Sonra, yeni değişken için kotanjantı u = ctg (x) seçiyoruz, diferansiyeli bize sadeleştirmemiz gereken çarpanı verecek. Yerine koyma işleminden sonra, entegre edildiğinde ark teğetini veren bir fonksiyona ulaşıyoruz. 
Pekala, u'yu kotanjant olarak değiştirmeyi unutma.
Örnek 25. Testin son görevinde bir çift açının kotanjantını 4. dereceye entegre etmeniz gerekiyor. 

Bunun üzerine entegrasyon testi çözülür ve tek bir öğretmen yanıtlarda ve dönüşümlerin gerekçesinde hata bulamaz.
Bu şekilde nasıl entegre edileceğini öğrenirseniz, integraller konusundaki testler veya bölümler sizin için fena olmaz. Diğer herkesin bizden (veya rakiplerimizden :))) integrallerin çözümlerini öğrenme veya sipariş etme fırsatı vardır.
Altında mantıksız%%x%% bağımsız değişkeninin veya %%n \in \mathbb(N)%% derecesinin %%P_n(x)%% polinomunun işaretinin altında olduğu bir ifadeyi anlayın radikal(Latince'den sayı tabanı- kök), yani kesirli kuvvete yükseltilmiştir. %%x%%'ye göre irrasyonel olan bazı integral sınıfları, değişkenin yeni bir değişkene göre rasyonel ifadelere değiştirilmesiyle azaltılabilir.
Bir değişkenin rasyonel fonksiyonu kavramı birkaç argümana genişletilebilir. %%u, v, \dotsc, w%% argümanlarının her biri üzerinden fonksiyonun değeri hesaplanırken sadece aritmetik işlemler ve bir tamsayı kuvvetine yükseltme sağlanırsa, bu argümanların rasyonel bir fonksiyonundan söz edilir. genellikle %%R (u, v, \ dotsc,w)%% ile gösterilir. Böyle bir fonksiyonun bağımsız değişkenleri, %%\sqrt[n](x), n \in \mathbb(N)%% biçimindeki radikaller dahil olmak üzere %%x%% bağımsız değişkeninin işlevleri olabilir. Örneğin, %%u = x, v = \sqrt(x)%% ve %% için $$ R(u,v,w) = \frac(u + v^2)(w) $$ rasyonel işlevi w = \sqrt(x^2 + 1)%%, $$ R\left(x, \sqrt(x), \sqrt(x^2+1)\right) = \frac(x + \sqrt(x ^2))(\sqrt(x^2 + 1)) = f(x) $$ of %%x%% ve radikaller %%\sqrt(x)%% ve %%\sqrt(x ^2 + 1 )%%, %%f(x)%% işlevi ise bir bağımsız değişken olan %%x%%'nin irrasyonel (cebirsel) bir işlevi olacaktır.
%%\int R(x, \sqrt[n](x)) \mathrm(d)x%% biçimindeki integralleri düşünün. Bu tür integraller, %%t = \sqrt[n](x)%%, ardından %%x = t^n, \mathrm(d)x = nt^(n-1)%% değişkeni değiştirilerek rasyonalize edilir.
örnek 1
%%\displaystyle\int \frac(\mathrm(d)x)(\sqrt(x) + \sqrt(x))%%'yi bulun.
İstenen bağımsız değişkenin integrali, %%2%% ve %%3%% dereceli köklerin bir fonksiyonu olarak yazılır. %%2%% ve %%3%%'ün en küçük ortak katı %%6%% olduğundan, bu integral %%\int R(x, \sqrt(x)) \mathrm(d) türünde bir integraldir. x %% ve %%\sqrt(x) = t%% değiştirilerek rasyonalize edilebilir. O zaman %%x = t^6, \mathrm(d)x = 6t \mathrm(d)t, \sqrt(x) = t^3, \sqrt(x) =t^2%%. Bu nedenle, $$ \int \frac(\mathrm(d)x)(\sqrt(x) + \sqrt(x)) = \int \frac(6t^5 \mathrm(d)t)(t^3 + t^2) = 6\int\frac(t^3)(t+1)\mathrm(d)t. $$ %%t + 1 = z, \mathrm(d)t = \mathrm(d)z, z = t + 1 = \sqrt(x) + %1 ve $$ \begin(array)(ll ) \int \frac(\mathrm(d)x)(\sqrt(x) + \sqrt(x)) &= 6\int\frac((z-1)^3)(z) \mathrm(d) t = \\ &= 6\int z^2 dz -18 \int z \mathrm(d)z + 18\int \mathrm(d)z -6\int\frac(\mathrm(d)z)(z ) = \\ &= 2z^3 - 9 z^2 + 18z -6\ln|z| + C = \\ &= 2 \left(\sqrt(x) + 1\sağ)^3 - 9 \left(\sqrt(x) + 1\sağ)^2 + \\ &+~ 18 \left( \sqrt(x) + 1\sağ) - 6 \ln\left|\sqrt(x) + 1\sağ| + C \end(dizi) $$
%%\int R(x, \sqrt[n](x)) \mathrm(d)x%% şeklindeki integraller, doğrusal-kesirli irrasyonalitelerin özel bir durumudur, yani %%\displaystyle\int R\left(x, \sqrt[n](\dfrac(ax+b)(cd+d))\right) \mathrm(d)x%% şeklinde integraller, burada %% ad - bc \neq %0 %%%t = \sqrt[n](\dfrac(ax+b)(cd+d))%% değişkeni değiştirilerek rasyonalize edilebilir, ardından %%x = \dfrac( dt^n - b)(a - ct^n)%%. Sonra $$ \mathrm(d)x = \frac(n t^(n-1)(ad - bc))(\left(a - ct^n\right)^2)\mathrm(d)t. $$
Örnek 2
%%\displaystyle\int \sqrt(\dfrac(1 -x)(1 + x))\dfrac(\mathrm(d)x)(x + 1)%%'yi bulun.
%%t = \sqrt(\dfrac(1 -x)(1 + x))%%, sonra %%x = \dfrac(1 - t^2)(1 + t^2)%%, $ alalım $ \begin(array)(l) \mathrm(d)x = -\frac(4t\mathrm(d)t)(\left(1 + t^2\right)^2), \\ 1 + x = \ frac(2)(1 + t^2), \\ \frac(1)(x + 1) = \frac(1 + t^2)(2). \end(array) $$ Bu nedenle, $$ \begin(array)(l) \int \sqrt(\dfrac(1 -x)(1 + x))\frac(\mathrm(d)x)(x + 1) = \\ = \frac(t(1 + t^2))(2)\left(-\frac(4t \mathrm(d)t)(\left(1 + t^2\right)^2) )\right) = \\ = -2\int \frac(t^2\mathrm(d)t)(1 + t^2) = \\ = -2\int \mathrm(d)t + 2\int \frac(\mathrm(d)t)(1 + t^2) = \\ = -2t + \text(arctg)~t + C = \\ = -2\sqrt(\dfrac(1 -x)( 1 + x)) + \text(arctg)~\sqrt(\dfrac(1 -x)(1 + x)) + C. \end(dizi) $$
%%\int R\left(x, \sqrt(ax^2 + bx + c)\right) \mathrm(d)x%% biçimindeki integralleri düşünün. En basit durumlarda, tam kare seçildikten sonra değişkenlerde bir değişiklik yapılırsa, bu tür integraller tablosal olanlara indirgenir.
Örnek 3
%%\displaystyle\int \dfrac(\mathrm(d)x)(\sqrt(x^2 + 4x + 5))%% integralini bulun.
%%x^2 + 4x + 5 = (x+2)^2 + %1% olduğuna göre, %%t = x + 2, \mathrm(d)x = \mathrm(d)t%% alırız, sonra $$ \begin(array)(ll) \int \frac(\mathrm(d)x)(\sqrt(x^2 + 4x + 5)) &= \int \frac(\mathrm(d)t) (\sqrt(t^2 + 1)) = \\ &= \ln\left|t + \sqrt(t^2 + 1)\sağ| + C = \\ &= \ln\left|x + 2 + \sqrt(x^2 + 4x + 5)\sağ| + C. \end(dizi) $$
Daha karmaşık durumlarda, %%\int R\left(x, \sqrt(ax^2 + bx + c)\right) \mathrm(d)x%% biçimindeki integralleri bulmak için şunu kullanırız:
Kesirlerin ve köklerin integrallerini ele almaya devam ediyoruz. Hepsi süper karmaşık değil, sadece bir nedenden ötürü, örnekler diğer makalelerde biraz "konu dışı" idi.
Örnek 9
belirsiz integrali bulun
Kökün altındaki paydada, "x" şeklinde kök "ek" dışında bir kare üçlü artı artı vardır. Bu formun bir integrali, standart bir ikame kullanılarak çözülür.
![]() .
.
Değiştirme basittir:
![]()
Değişimden sonra hayata bakmak:

(1) Yerine koyma işleminden sonra kök altındaki terimleri ortak bir paydaya indirgeriz.
(2) Kökün altından çıkarıyoruz.
(3) Pay ve paydayı azaltıyoruz. Aynı zamanda kök altında terimleri uygun bir düzende yeniden düzenledik. Biraz deneyimle, (1), (2) adımları, yorumlanan eylemler sözlü olarak gerçekleştirilerek atlanabilir.
(4) Ortaya çıkan integral, hatırladığınız gibi çözüldü. tam kare seçim yöntemi. Tam bir kare seçin.
(5) Entegrasyonla sıradan bir "uzun" logaritma elde ederiz.
(6) Tersine değiştirmeyi gerçekleştiriyoruz. Başlangıçta ise, sonra geri: .
(7) Nihai eylem, sonucu düzeltmeyi amaçlamaktadır: kökün altında, terimleri tekrar ortak bir paydaya getiriyoruz ve kökün altından çıkarıyoruz.
Örnek 10
belirsiz integrali bulun
![]() .
.
Bu bir kendin yap örneğidir. Burada, yalnız x'e bir sabit eklenir ve değiştirme hemen hemen aynıdır:
![]() .
.
Gereken tek şey, yapılan değiştirmeden "x"i ek olarak ifade etmektir:
![]() .
.
Dersin sonunda tam çözüm ve cevap.
Bazen böyle bir integralde kökün altında bir kare binom olabilir, bu çözümün çözülme şeklini değiştirmez hatta daha da basit olacaktır. Farkı Hisset:
Örnek 11
belirsiz integrali bulun
Örnek 12
belirsiz integrali bulun
Dersin sonunda kısa çözümler ve cevaplar. Örnek 11'in tam olarak binom integrali, çözümü derste ele alınan İrrasyonel fonksiyonların integralleri.
Derecenin paydasında ayrıştırılamayan 2. dereceden bir polinomun integrali
Daha nadir, ancak yine de, integralin pratik örneklerinde ortaya çıkan bir form.
Örnek 13
belirsiz integrali bulun
İntegrandın paydası ayrıştırılamaz bir kare binom içerir. Faktörlere ayrılamazlığın önemli bir özellik olduğunu vurguluyoruz. Polinom çarpanlarına ayrılırsa, her şey çok daha nettir, örneğin:
Şanslı sayı 13 ile örneğe geri dönelim. Bu integral aynı zamanda, nasıl çözüleceğini bilmiyorsanız oldukça fazla acı çekebileceğinizler kategorisindendir.
Çözüm, yapay bir dönüşümle başlar:

Bence herkes payın paydaya terim terime nasıl bölüneceğini zaten anlıyor.
Ortaya çıkan integral parçalar halinde alınır:


Formun bir integrali için
nerede ( k≥ 2) türetilmiş bir doğal sayıdır yinelenen düşürme formülü:
![]() ; derecesi 1'den küçük olan bir integraldir.
; derecesi 1'den küçük olan bir integraldir.
Payda ek bir polinom varsa ne olur? Bu durumda, belirsiz katsayılar yöntemi kullanılır ve integral kesirlerin toplamına genişletilir. Böyle bir integral oluşursa, ders kitabına bakın - orada her şey basit.

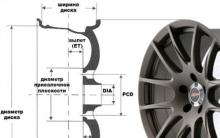
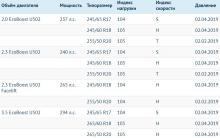




Bir dizüstü bilgisayarda Skype'ı nasıl geri yükleyeceğimizi düşünüyoruz.
Fixies ustaları tam sürüm Fixies oyunu tam sürüm bilgisayarınıza indirin
Net framework 3 hatalarını yükleme veya güncelleme, düzeltme
Dünyadaki sanal para birimleri ve sanal borsalar
Altın Numaralar Güzel bir telefon numarası nasıl satılır