Çıkış koordinatlarının vektörünün oluşumunda bir sistem gözlemlenebilir olarak adlandırılır. durum değişkenleri vektörünün tüm bileşenleri dahil edilir. Vektörün bileşenlerinden hiçbiri sistemin çıktısının oluşumunu etkilemiyorsa, böyle bir sistem gözlemlenemez olacaktır.

Kontrol edilebilirlik ve gözlemlenebilirlik analizi kullanılarak gerçekleştirilir kontrol edilebilirlik matrisleri ve gözlenebilirlik veya kullanarak gramer kontrol edilebilirliği ve gözlenebilirlik.

Matrisler bazında iki yardımcı matris oluşturalım.

r = [ , , ..., n-1 ], NS= [,, ..., n -1]

matrisler r ve NS buna göre adlandırılır kontrol matrisi ve gözlemlenebilirlik matrisi sistemler. MATLAB paketinde komutlar kullanılarak oluşturulabilirler. ctrb ve obsv.

Sistemin (3.2) kontrol edilebilir olması için gerekli ve

kontrol edilebilirlik matrisinin tam sıraya sahip olması yeterlidir. rütbeR = n.

(3.2) sisteminin gözlenebilir olması için gözlenebilirlik matrisinin tam sıralı olması gerekli ve yeterlidir. sıraD = n.

Matrisin bir girişi ve bir çıkışı olan sistemler olması durumunda r ve NS karedir, bu nedenle, kontrol edilebilirliği ve gözlemlenebilirliği kontrol etmek için, R ve D matrislerinin determinantlarını hesaplamak yeterlidir. Eğer sıfıra eşit değillerse, matrisler tam ranklıdır.

Ders 4. ACS işleyişinin değerlendirilmesi

Statik özelliklerin değerlendirilmesi

ACS'de meydana gelen süreçlere bağlı olarak, ACS'nin ve elemanlarının iki çalışma modu ayırt edilir: dinamik ve statik.

Geçici süreç, ACS'nin ve öğelerinin dinamik çalışma moduna karşılık gelir. TAU'da çoğu zaman bu moda ayrılmıştır. Dinamik modda, ACS'nin durumunu belirleyen değerler ve elemanları zamanla değişir. Yukarıda, otomatik kontrol sisteminin dinamik moddaki matematiksel modelleri diferansiyel denklemler şeklinde sunulmuştur. n-th (2.1) veya durum denklemleri (3.2, 3.3) şeklinde.

Aksine, ACS'deki kararlı durum süreci, ACS'nin durumunu karakterize eden değerlerin zamanla değişmediği statik bir çalışma moduna karşılık gelir. ACS'yi statik (sabit durum) modda değerlendirmek için kontrol doğruluğu adı verilen bir gösterge kullanılır. Bu gösterge, ACS'nin statik özellikleri tarafından belirlenir.

Pirinç. 4.1. Statik ve astatik sistemlerin statik özellikleri

ACS'nin statik özelliği, çıkış parametresinin kararlı durum değerinin bağımlılığını temsil eder. - y 0 giriş parametresinden - sen 0 sabit bozulma veya çıkış parametresinin bağımlılığı ile - 0 pertürbasyondan kararlı durumda - F sabit giriş parametresi ile. ACS'nin statik denklemleri şu şekildedir: veya ... Genel olarak, denklemler doğrusal olmayabilir. İkinci denkleme göre oluşturulmuş elemanların veya bir bütün olarak ACS'nin (Şekil 4.1) statik özelliklerini düşünün. Sistemdeki hatanın kararlı durum değeri, bozukluğun kararlı durum değerine bağlıysa F, o zaman sistem statik olarak adlandırılır (Şekil 4.1, a) ve bağımlı değilse, o zaman astatiktir (Şekil 4.1, b).

Sistemin göreli statik hatası veya devletçiliği,

Ayrıca, devletçilik, statik özelliğin eğiminin tanjantına eşit olan devletçilik katsayısı ile karakterize edilebilir (Şekil 3.1, a).

ACS'nin sabit durumda statik kontrolünün etkinliği, otomatikleştirilmemiş kontrol nesnesinin (kontrolör olmadan) mutlak statik hatasının oranına eşit olan sözde kontrol doğruluğu derecesi ile tahmin edilir. otomatik sistemin mutlak statik hatası.

Bazı durumlarda, statik bir hata istenmez, daha sonra astatik düzenlemeye geçerler veya bozulmalar üzerinde dengeleyici etkiler oluştururlar.

V.N. Nepopalov

Durum değişkeni yöntemi

öğretici

Çelyabinsk 2003

UDC 621.3.011 (075.8)

Nepopalov V.N. Durum değişkenlerinin yöntemi: Ders kitabı. - Nizhnevartovsk, Ed. 2003. - 26 s.

Doğrusal elektrik devrelerinde geçici süreçleri hesaplamak için durum değişkenleri yöntemi göz önünde bulundurulur. Ders kitabı, öğrencilere "Elektrik mühendisliğinin ek bölümleri" dersinde bağımsız çalışma konusunda yardımcı olmayı amaçlamaktadır.

1. Durum 4 denklemlerinin normal formu

2. Durum 5 denklemlerinin normal formunun elde edilmesi

3. Durum 6'nın normal denklem formunu elde etme örnekleri

4. Hal denklemlerinin klasik yöntemle çözülmesi 9

5. Durum denklemlerini çözmek için matris teorisinin öğelerini kullanma 15

6. Geçici olayların hesaplanmasına uygulama 22

7. Kontrol soruları 24

Durum değişkeni yöntemi

Durum değişkenleri t zamanında tanımlanır 0 değerleri için belirtilenlerle birlikte bir dizi fonksiyon (voltajlar, akı bağlantıları, akımlar veya yükler)T T 0 girdi eylemleri, herhangi bir an için çıktı işlevlerini açık bir şekilde belirlemek yeterlidirT T 0 .

Kesin olarak o an için, yani anahtarlamadan hemen sonra tanımlanan belirli bir dizi voltaj, yük, akım veya akı bağlantıları, elektrik devresinin durum değişkenleri olarak seçilebilir. Bu durum, kapasitörlerdeki voltajlar veya yükler ve indüktörlerdeki akımlar veya akı bağlantıları ile durum değişkenlerini seçme olasılığını sınırlar, çünkü bu miktarların değerleri anahtarlama anında değişmez T  0:

,,,.

Durum değişkenlerinin sayısını belirleyen niceliklerin sayısı, bağımsız fiziksel başlangıç ​​koşullarının sayısına eşittir.

1. Normal hal denklemleri

Durum değişkenleri zaman içinde bir noktada T belirlenir sütun matrisi
, boyut

Durum değişkenlerinin yardımıyla, zamandan bağımsız parametrelere sahip doğrusal bir elektrik devresinin matematiksel modeli bir dizi diferansiyel denklem ile belirlenir:

ve cebirsel denklemler:

nerede x(T) Boyutlu durum değişkenlerinin bir matris sütunudur
;

durum değişkenlerinin türevlerinin matris sütunu;

F(T) - verilen girdi değişkenlerinin veya girdi eylemlerinin matris sütunu;

Y(T)– çıktı değişkenlerinin matris sütunu;

A,V,İLE BİRLİKTE,NS- bilinen miktarların matrisleri ve, A- kare düzen matrisi n... matrislerin boyutları M.Ö, NS belirli bir problemin koşulları tarafından belirlenir.

Formun diferansiyel denklemleri

durum denklemlerinin normal formu ve formun cebirsel denklemleri olarak adlandırılacaktır.

çıkış fonksiyonlarının denklemleri.

2. Durum denklemlerinin normal formunun elde edilmesi

Durum denklemlerinin normal formunu elde etmek için

1. Devre şemasının yönlendirilmiş bir grafiğini çizin. Bu grafik için normal bir ağaç oluşturun. Normal bir ağaçta şunları eklemeniz gerekir: kapları ve kaynakları olan tüm şubeler e. ile birlikte... Bu bir ağaç elde etmek için yeterli değilse, dirençlerle dallar ekleyin, bu bir ağaç elde etmek için yeterli değilse, indüktörlerle dallar ekleyin. Grafiğin bağlantıları (kordları), endüktanslı dallar, akım kaynakları ve grafik ağacına dahil olmayan dirençli dallar olmalıdır.

2. Ağacın her dalı için, ağacın yalnızca bir dalı ve belirli bir dizi grafik bağlantılarını (kordlar) içeren bir bölüm belirleyin. Bağımsız bölüm sayısı ağaç dalı sayısına eşittir: B T  Q - 1, nerede - Q düğüm sayısı. Her ana bölümün akımları için Kirchhoff denklemlerini yazın ve ağacın dallarının akımlarını kirişlerin dallarının akımları cinsinden ifade edin. Ana denklemler, kapasitans akımlarını (varsa) içeren denklemlerdir.

3. Her bağlantı için, yalnızca bir bağlantı ve belirli bir ağaç dalı kümesi içeren bir kontur tanımlayın. Bağımsız konturların sayısı, bağlantıların sayısına eşittir: B ben  b - q + 1, nerede B– grafiğin dallarının sayısı. Her devre için ikinci Kirchhoff yasasına göre denklemleri yazın ve indüktörler (varsa) üzerindeki gerilimleri diğer elemanlar üzerindeki gerilimler cinsinden ifade edin. Bağlantılar akım kaynaklarına sahip dallarsa, durum denklemleri hazırlanırken, bu devreler için ikinci Kirchhoff yasasına göre denklemler yazılmaz. Ana denklemler, indüktörler arasındaki voltajları içeren denklemlerdir.

4. Kalan denklemlerin yardımıyla, direnç dallarının gerilimlerini ve akımlarını temel denklemlerden çıkarın. Kapasitans akımlarını ve endüktans voltajlarını, kapasitans voltajları ve endüktans akımları aracılığıyla ifade edin.

5. Elementlerin denklemlerini temel denklemlerle değiştirin:

;
.

6. Ortaya çıkan sistemi, durum denklemlerinin normal biçimine dönüştürün.

7. Çıkış fonksiyonlarının cebirsel denklemlerini yazın.

Durum değişkeni yöntemi (durum uzayı yöntemi olarak da adlandırılır), matris biçiminde yazılmış iki denkleme dayanır.

Birinci denklemin yapısı, durum değişkenlerinin ilk zaman türevlerinin matrisini, durum değişkenlerinin kendi matrisleri ve e olarak kabul edilen dış etkiler ile bağlaması ile belirlenir. vb. ile. ve kaynak akımları.

İkinci denklem yapı olarak cebirseldir ve çıktı miktarları y matrisini durum değişkenleri ve dış etkilerin matrisleri ve ile birleştirir.

Durum değişkenlerini tanımlarken, aşağıdaki özelliklerini not ederiz.

1. Elektrik devrelerinde durum değişkenleri olarak, indüktörlerdeki akımlar ve kapasitörlerdeki voltajlar seçilmelidir ve tüm endüktanslarda ve tüm kapasitelerde değil, yalnızca bağımsız olanlar için, yani sistemin genel sırasını belirleyenler için seçilmelidir. devrenin diferansiyel denklemleri.

2. Zincirin durum değişkenlerine göre diferansiyel denklemleri kanonik biçimde yazılır, yani durum değişkenlerinin zamana göre birinci türevlerine göre çözülmüş olarak gösterilirler.

Durum değişkenleri olarak yalnızca bağımsız endüktanslardaki ve bağımsız kapasitörlerdeki gerilimlerdeki k akımlarının durumu seçildiğinde, durum değişkeni yönteminin ilk denkleminin yukarıdaki yapıya sahip olacağına dikkat edin.

Kapasitörlü dallardaki akımlar veya dirençli dallardaki akımlar ve ayrıca indüktörlerdeki voltajlar veya dirençlerdeki voltajlar durum değişkenleri olarak seçilirse, durum değişkenleri yönteminin ilk denklemi kanonik biçimde de gösterilebilir, yani, Bu değerlerin ilk zaman türevlerine göre çözülmüştür. Bununla birlikte, sağ taraflarının yapısı, dış etkilerin birinci türevlerinin matrisini de içereceğinden, yukarıda verilen tanıma karşılık gelmeyecektir.

3. Durum değişkenlerinin sayısı, incelenen elektrik devresinin diferansiyel denklem sisteminin sırasına eşittir.

4. Değişken olarak akım ve voltaj durumunun seçimi de uygundur, çünkü bu miktarlar, komütasyon yasalarına göre (§ 13-1), komütasyon anında aniden değişmez, yani aynıdırlar. zamanın anları için

5. Durum değişkenleri böyle adlandırılır çünkü her an elektrik devresinin enerji durumunu ayarlarlar, çünkü ikincisi ifadelerin toplamı ile belirlenir

6. Denklemlerin kanonik formda gösterilmesi, analog bilgisayarlarda çözülürken ve sayısal bilgisayarlarda çözülürken programlama için çok uygundur. Bu nedenle, modern bilgisayar teknolojisinin yardımıyla bu denklemleri çözerken böyle bir temsil çok önemlidir.

Şekildeki devre örneği ile gösterelim. 14-14 Durum değişkenli denklemlerin nasıl oluşturulduğu.

İlk olarak, yöntemin ilk matris denklemine karşılık gelen bir diferansiyel denklem sistemi elde ediyoruz ve ardından bunu matris biçiminde yazıyoruz. Herhangi bir elektrik devresi için bu denklemleri derleme algoritması aşağıdaki gibidir. İlk olarak, denklemler Kirchhoff yasalarına göre veya döngü akımları yöntemiyle yazılır; daha sonra durum değişkenleri seçilir ve orijinal denklemlerin türevleri alınarak ve diğer değişkenler ortadan kaldırılarak elde edilir.

durum değişkenleri yönteminin denklemleri bulunur. Bu algoritma, değişkenlerden birine göre bir sonuç diferansiyel denklemi elde etmek için geçici süreçleri hesaplamak için klasik yöntemde kullanılana çok benzer.

Özel durumlarda, devrede kapasitif devreler olmadığında, yani tüm dalları kapasite içeren devreler ve her birinde indüktör bulunan bağlı dallara sahip düğümler olmadığında, başka bir algoritma da belirtilebilir. Üzerinde durmadan, sadece kapların emülsiyon kaynaklarıyla değiştirilmesine dayandığını not ediyoruz. vb., indüktörler - akım kaynakları ve süperpozisyon yönteminin uygulanması.

Zincir için şek. Kirchhoff yasalarına göre 14-14

(14-36)

Birinci denklemden belirleme, üçüncüde yerine koyma, ortaya çıkan diferansiyel denklemi değiştirme ve kanonik formda sunma ile elde ederiz:

İkinci denklemi (14-36) göre çözerek, birinci denkleme (14-36) göre değiştirerek ve değiştirerek şunu elde ederiz:

Terim terim (14-38) toplanarak denklem (14-37) ile çarpılır ve elde edilen sonuçtan belirlenir, şunu elde ederiz:

(14-39) ve (14-37) denklemlerini matris biçiminde yeniden yazalım:

(14-4 °)

düşünülen zincir için elimizde:

(14-42a)

Genel durumda, durum değişkenleri yönteminin matris formundaki ilk denklemi şu şekilde yazılır:

(14-43)

Lineer devrelerde A ve B matrisleri sadece devrenin parametrelerine bağlıdır, yani sabit değerlerdir. Bu durumda A, mertebenin kare matrisidir ve zincirin ana matrisi olarak adlandırılır, matris B genellikle dikdörtgendir, boyuta zincirin girişi ile durum değişkenleri arasındaki bağlantı matrisi denir, matrisler sütundur. durum değişkenlerinin matrisleri veya vektörleri (boyut ve dış rahatsızlıklar (boyut)

Söz konusu örnekte, durum değişkenlerinin sayısı dış düzensizliklerin sayısına eşit olduğundan, B matrisinin ikinci mertebeden kare olduğu ortaya çıktı.

Gelelim yöntemin ikinci denkleminin derlenmesine.Değerlerden herhangi biri çıktı olarak seçilebilir. Örneğin, çıktı olarak üç miktar alın

Değerleri doğrudan denklemlerden durum değişkenleri ve dış rahatsızlıklar cinsinden yazılabilir (14 36)

(14-44)

veya matris formunda

veya kısaltılmış

(14-46)

düşünülen zincir için nerede

ve genel durumda durum değişkenleri yönteminin ikinci denklemi

Matrisler C ve D sadece devrenin parametrelerine bağlıdır. Genel durumda, bunlar karşılık gelen boyutlarda dikdörtgen matrislerdir ve C, durum değişkenlerinin devrenin çıkışıyla bağlantı matrisi, devrenin (veya sistemin) giriş ve çıkışının doğrudan bağlantısının matrisi olarak adlandırılır.

Bir dizi fiziksel sistem için, D bir sıfır matrisidir ve (14-48)'deki ikinci terim, doğrudan bir matris olmadığı için yok olur. Sistemin giriş ve çıkışı arasındaki iletişim.

Örneğin, akım i ve voltajı durum değişkenleri olarak alırsak ve bunlar için diferansiyel denklemleri kanonik biçimde temsil edersek, o zaman (tüm ara dönüşümleri atlayarak) matris biçimindeki yöntemin denklemlerinden ilki şu şekilde olacaktır:

Bu nedenle, aslında, durum değişkenleri yönteminin ilk denklemi, yalnızca akım ve voltaj durumları değişken olarak seçilirse matris formunda (14-43) formuna sahip olacaktır.

Matris diferansiyel denkleminin (14-43) çözümüne geçerken, öncelikle kare temel matris A'nın diyagonal olması durumunda özellikle basitleştirildiğini not ediyoruz. Daha sonra tüm lineer diferansiyel denklemler (14-43) ayrıştırılır, yani durum değişkenlerinin türevleri her biri yalnızca kendi durum değişkenine bağlıdır.

Önce lineer homojen olmayan matris diferansiyel denkleminin (14-43) operatör yöntemiyle çözümünü ele alalım.Bunu yapmak için Laplace'a göre dönüştürüyoruz:

ayrıca, durum değişkenlerinin ilk değerlerinin sütun matrisi, yani.

(14-53)

anahtarlama anında aniden değişmeyen, verilen ve o andaki değerlerine eşit olan

Yeniden yazalım (14-51):

birim sıra matrisi nerede.

Durum değişkenlerinin görüntülerinden oluşan bir matris elde etmek için, soldaki her iki tarafı (14-54) ters matrisle çarpıyoruz.

Ters Laplace dönüşümünü kullanarak orijinallere geri dönersek, şunu elde ederiz:

Operatör yönteminden bilinmektedir ki

Analojiyle, ters Laplace dönüşümünü matris biçiminde yazarsak, şunu elde ederiz:

sistemin durumunun geçiş matrisi nerede, aksi takdirde temel olarak adlandırılır.

Böylece birinci terimin aslını sağ tarafta (14-56) buluyoruz.

Ters matris, ilişkili veya karşılıklı matrisin ana matrisin determinantına bölünmesiyle belirlenir:

denklem nerede

(14-61)

incelenen devrenin karakteristik denklemidir.

(14-56)'nın sağındaki ikinci terimin aslı matris formunda evrişim teoremi kullanılarak bulunur.

eğer koyarsak

Daha sonra (14-62) - (14-64)

ve (14-56), (14-59) ve (14-65)'e dayalı diferansiyel homojen olmayan matris denkleminin (14-43) genel çözümü şu şekilde olacaktır:

(14-66)

Sağ taraftaki ilk terim (14-66) durum değişkenlerinin değerlerini veya devrenin sıfır girişteki tepkisini yani başka bir deyişle devredeki serbest işlemlerin ilk bileşenini temsil eder. Devrenin durum değişkenlerinin sıfır olmayan başlangıç ​​değerleri nedeniyle ve bu nedenle denklemin bir çözümüdür. İkinci terim, zincir reaksiyonunun, yani zincirin sıfır durumundaki bileşenidir.

Bir devrenin sıfır durumu, tüm durum değişkenlerinin başlangıç ​​değerleri sıfıra eşit olduğunda böyle bir durumdur. Başka bir deyişle, ikinci terim (14-66), dış etkilerin etkisi altında ortaya çıkan zincirin zorunlu reaksiyonu sırasındaki toplam ve serbest süreçlerin ikinci bileşenidir.

Eşitlik (14-66), zincirin reaksiyonunun sıfır giriş ve sıfır durumdaki reaksiyonların toplamına eşit olduğu anlamına gelir.

Elimizdeki çıkış değerleri için (14-48) ve (14-66) esas alınmıştır.

Zincirin durumu o anda değil, o anda belirtilirse, (14-66) ve (14-67) eşitlikleri genelleştirilir:

(14-68)

Örnek 14-5. İkinci dereceden dallanmış bir devre için durum denklemleri yazılır

sıfır olmayan başlangıç ​​koşulları ve tek bir e kaynağı ile. vb. ile.

Durum değişkenlerini bulun.

Çözüm. Durum denklemlerini matris formunda yeniden yazalım

İlk olarak sıfır girişte durum değişkenlerinin ilk serbest bileşenlerini bulalım. Bunun için matrisi oluşturuyoruz.

Bitişik veya karşılıklı matrisi bulmak için önceki matristeki her bir elemanı cebirsel tümleyeni ile değiştirin.Matrisi elde ederiz.

İlişkili veya karşılıklı matrisi bularak onu değiştiririz:

Matrisin determinantını bulun

(14-60)'a göre matrisin tersi şu şekilde olacaktır:

Bunun için her bir öğesinin ters Laplace dönüşümüne tabi tutulması gerektiği gerçeğini göz önünde bulundurarak, onu ters Laplace dönüşümüne tabi tutalım. (14-73)'e dayanarak, devrenin durumunun geçiş matrisini elde ederiz.

Örneğin,

Sistemin durumunun geçiş matrisi için şunu elde ederiz:

Durum değişkenlerinin ilk serbest bileşenleri için,

Elde edilen sonuçları özetleyerek, durum değişkenlerinin istenen değerlerini buluyoruz:

Denklemin (14-43) çözümü yukarıda elde edildiğinden ve formül (14-66) ile verildiğinden, daha sonra çözümün doğruluğunu kontrol etmek (14-66) ve durum değişkenlerinin matrisini onunla hesaplamak için, önce doğrudan yerine koyabilirsiniz. (14-66)'ya ( 14-43) ikincinin bir kimliğe dönüşmesini sağlayın. Bunu yapmak için önce (14-66) türevini alarak hesaplamanız yeterlidir. Bu durumda şunu elde ederiz:

Artık (14-66) matris diferansiyel denkleminin bir çözümü olduğunu doğrudan doğrulamak kolaydır.

Em sisteminin durumunun geçiş matrisinin durum uzayında, yani boyutların sayısı durum değişkenleri vektörünün bileşenlerinin sayısına eşit olan uzayda, yer değiştirme başlangıcını bulmamıza izin verdiğine dikkat edin. bazı başlangıç ​​konumundan (at veya at) ve vektör önemli bilgiler içerir, çünkü aynı anda tüm durum değişkenlerini, yani zamanın işlevlerini tanımlar.

Durum denklemleri, devrenin modunu belirleyen herhangi bir denklem sistemi olarak adlandırılabilir. Daha dar anlamda, türevlere göre çözülen birinci mertebeden diferansiyel denklemler sistemidir.

Durum değişkenleri yöntemine, Cauchy formunda yazılmış (birinci dereceden) durum denklemlerinin çözümüne dayanan bir zincirin analizi denir. Bu nedenle, durum değişkenleri yöntemi, her şeyden önce geçici süreçleri hesaplama yöntemlerinden biridir. Ayrıca devrenin yalnızca bağımsız kaynaklara sahip olduğu ve endüktif bölümler ve kapasitif devreler içermediği varsayılmıştır. Aksi takdirde, denklem yazmak çok daha zor hale gelir.

Sabit toplu parametrelere sahip bir lineer devre için, her dalın akımı, seçilen terminaller arasındaki voltaj, kapasitör plakalarındaki yük vb. her zaman derlenen akım, voltaj, yük vb. için bir çözüm olarak bulunabilir. bu diferansiyel denklem için (örneğin, Kirchhoff denklemleri sisteminden diğer akımları ve voltajları hariç tutarak):

Değişkenleri tanıtarak, bu denklem eşdeğer bir birinci mertebeden diferansiyel denklem sistemine indirgenir:

Burada durum değişkenleri adı verilen değişkenler x ve türevleridir.

Bildiğiniz gibi, parametreleri (r, L, C, M değerleri) ve çalışma kaynakları dışında herhangi bir devredeki geçici süreç, bağımsız başlangıç ​​(t = 0) koşulları - endüktif elemanlardaki akımlar ve voltajlar ile belirlenir. Bilinmesi veya hesaplanması gereken kapasitif elemanlar üzerinde. Aranan değerler, geçiş sürecinde bunlar aracılığıyla ifade edilir. Ayrıca zincirin enerji durumunu da belirlerler. Bu nedenle, durum değişkenleri olarak akımların ve gerilimlerin seçilmesi tavsiye edilir. İşletim kaynakları girdi miktarları olarak adlandırılabilir , aranan değerler çıktıdır ... n tane bağımsız akım ve gerilime sahip bir devre için, n tane daha bağımsız başlangıç ​​koşulu belirtilmelidir.

Kısaca, durumun diferansiyel denklemlerini matris formunda aşağıdaki gibi yazarız:

veya daha kısa

burada X, durum değişkenlerinin (durum değişkenlerinin vektörü) bir sütun matrisidir (boyut n x 1); F - matris sütunu (boyut m x 1) EMF ve kaynak akımları (harici rahatsızlıklar); A - n dereceli kare matris (temel); B - n x m boyutunda matris (iletişim matrisi). Bu matrislerin elemanları topoloji ve devre parametreleri tarafından belirlenir.

Matris biçimindeki çıkış büyüklükleri için (endüktif akımlar ve kapasitif elemanlardaki gerilimler belirlenmemişse), cebirsel denklemler sistemi şu şekildedir:

veya daha kısa

burada W bir sütun matrisidir (l x 1 boyutunda); M - bağlantı matrisi (boyut l x n); N - bağlantı matrisi (boyut l x m).

Matris elemanları topoloji ve devre parametrelerine bağlıdır. Durum denklemleri için topoloji ve parametre değerlerine dayalı makine oluşum algoritmaları da geliştirilmiştir.

Matris biçiminde (14.91) denklemler, örneğin süperpozisyon yöntemi kullanılarak oluşturulabilir. Durum değişkenlerinin türevleri arasındaki bağımlılıkları elde etmek için, yani. ve durum değişkenlerinin yanı sıra devreye etki eden EMF ve kaynak akımları, durum değişkenlerinin verildiğini varsayacağız. Söz konusu devre, örneğin Şek. 14.41, a, verilen her akımın bir akım kaynağı tarafından temsil edildiği ve verilen her voltajın bir voltaj kaynağı (EMF) tarafından temsil edildiği eşdeğer bir akımla (Şekil 14.41.6) değiştirdikten sonra değiştiririz. Süperpozisyon yöntemini uygulayarak (pozitif yönler seçilir), voltajları ve akımları yazarız (önce kaynakların hareketini, sonra devrede hareket eden kaynakları dikkate alırız):

O zamandan beri

Elbette Kirchhoff denklemlerinden direnç elemanlarının akım ve gerilimleri hariç tutularak denklemler (14.93) elde edilebilir. Bununla birlikte, zincirin dallarının sayısındaki artışla Kirchhoff denklemlerinin ortak çözümü giderek daha hantal hale gelir.

Durum denklemleri doğrudan matris formunda oluşturulabilir.

Akım kaynağı ve EMF yoksa, yani F = 0, denklemler (14.91) basitleştirilir

ve zincirdeki serbest süreçleri karakterize eder. Çözümü forma yazıyoruz.

nerede X (0) - durum değişkenlerinin ilk değerlerinin matris sütunu; - matris üstel işlevi.

(14.94)'ü (14.91c) yerine koyarak özdeşliğin elde edildiğinden emin olacağız.

Denklemi (14.91) çözerken, formda temsil ederiz

burada Ф (t) zincirin bazı matris fonksiyonudur. (14.95) türevini aldıktan sonra,

(14.96) ile (14.91а) karşılaştırın

ve integrasyondan sonra çarparak şunu buluruz:

q, entegrasyon değişkenidir veya

Bu ifadeyi (14.95) ile değiştirin:

Özellikle, t = 0 için

Bu nedenle, durum değişkenlerinin çözümü şu şekilde yazılır:

(zincirleme reaksiyon, sıfır giriş ve sıfır başlangıç ​​durumundaki reaksiyonların toplamına eşittir).

Bu çözüm, bölümde ele alınan geçişleri hesaplamak için operatör yöntemi uygulanarak elde edilebilir.

Çıkış miktarları (14.92) ile bulunabilir.

Zincirin durumu t = 0'da değil de 'de verilirse, o zaman (14.97)'de ilk terim şu şekilde yazılır: ve integralin alt sınırı 0 değil, t'dir.

Hesaplamanın ana zorluğu, matris üstel fonksiyonunun hesaplanmasında yatmaktadır. Yollardan biri şu şekildedir: ilk olarak, A matrisinin l ​​özdeğerlerini, yani denklemin köklerini buluyoruz.

burada 1 denklemden belirlenen n mertebesindeki birim matristir

A matrisinin elemanları nerede?

Özdeğerler, devrenin karakteristik denkleminin kökleri ile çakışır.

Argümanı n mertebesinde bir Аt matrisi olan bir matris üstel, sonlu sayıda n terimle temsil edilebilir. Özdeğerler farklıysa, o zaman

zamanın işlevleri nerede; vesaire.

Son olarak, (14.100)'den (14.99) belirledikten sonra X(t)'yi (14.97) buluruz.

Örnek 14.6. Şekildeki devredeki akımı belirleyin. 14.42'de geçiş yaptıktan sonra.

Çözüm. Endüktif elemanlarda, yani durum değişkenlerinde ve akımda akımların pozitif yönlerini seçiyoruz. Bağımsız başlangıç ​​koşulları:. diferansiyel devre denklemleri

Akımı ortadan kaldırarak, durum değişkenlerinin türevleri için denklemleri elde ederiz:

yani, (14.91)'e göre

ve başlangıç ​​değerlerinin sütun matrisi

Özdeğerleri hesaplayalım; tarafından (14.98)

nerede . Durum değişkenli denklemlerin ana belirleyicisini sıfıra eşitlersek, aynı değerleri alırız. .

(14.100) 'e göre ak katsayılarını, yani denklem sisteminden buluyoruz.

Anlarda hesaplanan güncel değerler sonunda akımın kararlı durumdan %1,5'ten daha az farklı olduğu 0 - 0,1 s zaman aralığı için saniyeler tabloda verilmiştir. 14.1. Hesaplamalarda, örnekte ve tabloda verilen tüm formüllerde sayılar 8 haneli yazılmıştır. 14.1 yuvarlama ile gösterilmiştir.

Tablo 14.1

A matrisinin n özdeğerleri arasında q katları varsa, n - q farklı kökler için sistem (14.100) derlenir ve q katları için ilk q - 1 türevleri hesaplandıktan sonra denklemler elde edilir. denklemin her iki tarafı da bir kök ile, yani

Zincirin tek bir rahatsız edici etkiye tepkisini bilmek, ör. geçici iletkenlik fonksiyonu veya / ve voltaj geçici fonksiyonu, devrenin isteğe bağlı bir şekle tepkisini bulabilirsiniz. Yöntem - Duhamel integralini kullanarak hesaplama yöntemi - süperpozisyon ilkesine dayanmaktadır.

Üzerinde entegrasyonun gerçekleştirildiği değişken ile devredeki akımın belirlendiği anı belirleyen değişkeni ayırmak için Duhamel integralini kullanırken, ilki genellikle, ikincisi ise t olarak gösterilir.

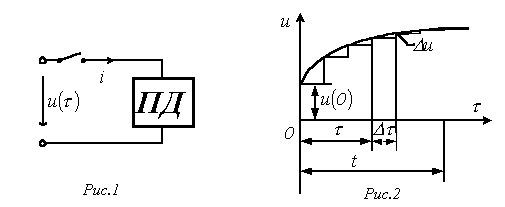
Sıfır başlangıç ​​koşullarına sahip devreye şu anda izin verin (pasif iki terminalli PD incirde. 1) keyfi voltajlı bir kaynak bağlı. Devredeki akımı bulmak için, orijinal eğriyi bir adımla değiştiririz (bkz. Şekil 2), ardından devrenin doğrusal olduğunu dikkate alarak, ilk voltaj sıçramasından ve tüm voltaj adımlarından gelen akımları toplarız. gecikmeli olarak yürürlüğe giren t anına kadar.

t zamanında, ilk voltaj sıçraması tarafından belirlenen toplam akımın bileşeni eşittir.

Şu anda, bir voltaj sıçraması var Atlamanın başlangıcından ilgili an t'ye kadar olan zaman aralığını hesaba katan , mevcut bileşeni belirleyecektir.

t zamanındaki toplam akım, dikkate alındığında, bireysel voltaj dalgalanmalarından gelen tüm akım bileşenlerinin toplamına açıkça eşittir, yani.

Zaman artışının sonlu aralığını sonsuz küçük bir aralıkla değiştirmek, yani. toplamdan integrale geçerek yazıyoruz

.

(1)

İlişki (1) denir Duhamel integrali.

Gerilmenin Duhamel integrali kullanılarak da belirlenebileceğine dikkat edilmelidir. Bu durumda (1)'de geçici iletkenlik yerine bir gerilim geçiş fonksiyonu olacaktır.

kullanarak hesaplama sırası
Duhamel integrali

Duhamel integralini kullanmanın bir örneği olarak, Şekil 2'de devredeki akımı tanımlıyoruz. 3 önceki derste dahil etme formülü kullanılarak hesaplanmıştır.

Hesaplama için ilk veriler: , , .

Elde edilen sonuç, dahil etme formülüne dayalı olarak önceki derste tanımlanan mevcut ifadeye benzer.

Durum değişkeni yöntemi

Elektromanyetik durum denklemleri, bir elektrik devresinin çalışma modunu (durumunu) belirleyen bir denklem sistemidir.

Durum değişkenleri yöntemi, türevlere göre çözülen birinci mertebeden diferansiyel denklemler sisteminin düzenli bir şekilde derlenmesine ve çözümüne dayanır, yani. bilgisayar teknolojisi ile uygulanan sayısal entegrasyon yöntemlerinin uygulanması için en uygun biçimde yazılmıştır.

Durum değişkenlerinin sayısı ve dolayısıyla durum denklemlerinin sayısı, bağımsız enerji depolama birimlerinin sayısına eşittir.

Durum denklemleri için iki ana gereksinim vardır:

denklemlerin bağımsızlığı;

Durum değişkenlerine (durum denklemlerinin yazıldığı değişkenler) dayalı olarak diğer değişkenleri kurtarma yeteneği.

İlk gereklilik, aşağıda ele alınacak olan durum denklemlerini hazırlamak için özel bir yöntemle karşılanmaktadır.

İkinci şartı yerine getirmek için, akı bağlantıları (endüktif elemanlı dallardaki akımlar) ve kapasitörlerdeki yükler (gerilimler) durum değişkenleri olarak alınmalıdır. Aslında, bu değişkenlerin zaman içindeki değişim yasasını bilerek, her zaman bilinen parametrelere sahip EMF ve akım kaynakları ile değiştirilebilirler. Devrenin geri kalanı dirençlidir ve bu nedenle her zaman kaynakların bilinen parametreleriyle hesaplanır. Ayrıca bu değişkenlerin başlangıç ​​değerleri bağımsızdır, yani. genel durumda, diğerlerinden daha kolay hesaplanırlar.

Durum değişkenleri yöntemiyle hesaplanırken, birinci türevleri ilişkilendiren durum denklemlerine ek olarak ve değişkenlerin kendileri ve dış etki kaynakları - EMF ve akım ile, aranan miktarları durum değişkenleri ve dış etki kaynakları ile birleştiren bir cebirsel denklem sistemi oluşturmak gerekir.

Böylece, matris formundaki tam denklem sistemi şu şekildedir:

;

(2)

.

(3)

Burada ve durum değişkenlerinin sütunlu matrisleri ve bunların ilk zaman türevleri sırasıyla; - dış etki kaynaklarının matris sütunu; - çıktı (aranan) değerlerinin sütunlu matrisi; - kare boyut nxn(burada n, durum değişkenlerinin sayısıdır) Jacobi matrisi olarak adlandırılan bir parametre matrisi; - kaynaklar ve durum değişkenleri arasındaki dikdörtgen bağlantı matrisi (satır sayısı n'ye eşittir ve sütun sayısı kaynak sayısına eşittir m); - durum değişkenlerinin gerekli değerlere sahip dikdörtgen bir bağlantı matrisi (satır sayısı gerekli değerlerin sayısına eşittir k ve sütun sayısı n'ye eşittir); - dikdörtgen boyut kxm girişten çıkışa iletişim matrisi.

Denklem (2) için başlangıç ​​koşulları, başlangıç ​​değerlerinin (0) vektörü ile verilir.

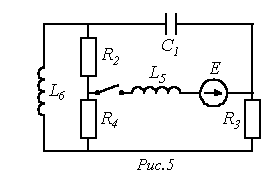
Durum denklemlerinin bir örneği olarak, Şekil 1'deki devreyi düşünün. 4, a, akımları belirlemek için gerekli olan ve.

Bu zincir için Kirchhoff'un yasalarına göre yazıyoruz

;

(5)

(3) biçimindeki bir matris denklemi, (4) ve (6) bağıntılarından gelir:

Başlangıç ​​değeri vektörü (0) =.

Karmaşık devreler için durum denklemlerini oluşturmak için Kirchhoff yasalarını doğrudan kullanmak zor olabilir. Bu bağlamda, durum denklemlerinin düzenli bir şekilde derlenmesi için özel bir teknik kullanılır.

Durum denklemlerini hazırlama yöntemi

Bu teknik aşağıdaki ana adımları içerir:

1. Tüm kapasitörleri ve voltaj kaynaklarını (EMF) kapsayan bir ağacın seçildiği devrenin yönlendirilmiş bir şeması çizilir (bkz. Şekil 4, b). Dirençler, gerektiği gibi ağaca dahil edilir: ağaçtaki tüm düğümleri kapsayacak şekilde. İletişim dalı indüktörleri, akım kaynaklarını ve kalan dirençleri içerir.

2. Grafiğin dallarının (ve devredeki elemanların) numaralandırılması aşağıdaki sırayla gerçekleştirilir: önce grafiğin kapasitörlü bölümleri (devreler) numaralandırılır, ardından ağaca dahil edilen dirençler, sonraki dirençlerle iletişim dalları ve son olarak endüktif elemanlara sahip dallar ( bkz. Şekil 4, b).

3. Devredeki elemanların bağlantısını açıklayan bir tablo derlenir. Tablonun ilk satırı (bkz. Tablo 1) ağacın kapasitif ve dirençli elemanlarının yanı sıra voltaj kaynaklarını (EMF) listeler. İlk sütun, akım kaynaklarının yanı sıra kuplaj dallarının dirençli ve endüktif elemanlarını listeler.

Tablo 1 . Bağlantı tablosu

Tabloyu doldurma prosedürü, bir kontur elde edilene kadar iletişim dallarının yardımıyla ağacın dallarının dönüşümlü olarak zihinsel olarak kapatılmasından ve ardından ilgili iletişim dalının yönüne göre ikincisinin çaprazlanmasından oluşur. “+” İşareti ile, yönü konturu geçme yönü ile çakışan grafiğin dalları ve “-” işareti ile zıt yönlü olan dallar yazılır.

Tablo sütunlara ve satırlara göre karalanmıştır. İlk durumda, birinci Kirchhoff yasasına göre, ikincisinde - ikincisine göre denklemler elde edilir.

İncelenen durumda (eşitlik önemsizdir)

,

nereden, orijinal devredeki akımların numaralandırılmasına göre

.

Pasif elemanlar üzerindeki voltaj hatları ile bağlantı tablosunu çizerken, tablonun karşısındaki işaretlerle almak gerekir:

(7)

Bu denklemler sırasıyla (6) ve (5) ilişkileriyle örtüşmektedir.

(7)'den hemen sonra gelir

.

Böylece, resmi bir şekilde, Kirchhoff yasaları kullanılarak yukarıda derlenenlere benzer denklemler elde edildi.

Edebiyat

1. Bessonov L.A. Elektrik mühendisliğinin teorik temelleri: Elektrik devreleri. Ders kitabı. üniversitelerin elektrik, enerji ve enstrüman yapımı uzmanlık öğrencileri için. –7. baskı, Rev. ve Ekle. –M.: Daha yüksek. shk., 1978. -528'ler.
2. Matkhanov P.N. Elektrik devresi analizinin temelleri. Doğrusal devreler.: Ders kitabı. elektrik mühendisliği için. radyo mühendisliği uzman. üniversiteler. 3. baskı, Rev. ve Ekle. –M.: Daha yüksek. okul., 1990. -400'ler.

Test soruları ve görevleri

A
V