Bir X kümesinde belirli bir Ω topolojisini tanımlamak için, Ω ailesinin tüm alt kümelerini doğrudan belirtmeye gerek yoktur. Taban kavramını kullanarak bir topoloji oluşturmanın çok uygun başka bir yolu daha var.
Uzayın (X, Ω) açık kümelerinin β koleksiyonuna denir. temel topolojiΩ veya temel uzay(X, Ω) ise topolojik uzayın her boş olmayan açık kümesi (X, Ω) β'ya ait bazı kümeler topluluğunun birleşimi olarak temsil edilebilir. Özellikle X, tüm taban kümelerinin birleşimine eşittir.
Teorem 1.9.
Ω topolojisinin açık kümelerinin β koleksiyonu, ancak ve ancak, herhangi bir açık küme U Ω ve herhangi bir х U noktası için, х V U olacak şekilde bir V β kümesi varsa, bu topolojinin temelidir.
Kanıt.Ω topolojisinin tabanı β olsun. U, Ω ailesinden rastgele bir açık kümedir, х, U kümesinin keyfi bir noktasıdır. O zaman, taban tanımına göre, küme, β koleksiyonuna ait bazı küme ailesinin olduğu kümedir. x U olduğundan, x V α0 β ve V α0 U olacak şekilde bir α 0 J indeksi vardır. Tersine, eğer U, Ω ailesinden rastgele bir açık küme ise, o zaman herhangi bir x U noktası için bir V x kümesi vardır. β öyle ki x V x U. Bu tür tüm V x'lerin birleşiminin U: ile çakıştığı doğrudan doğrulanır. Böylece, Ω ailesinden herhangi bir açık küme, β'ya ait bazı kümelerin birleşimidir. Bu nedenle, β, tanım gereği, Ω topolojisinin tabanıdır.
Teorem kanıtlanmıştır.
X'ten S α alt kümelerinden oluşan bir sisteme denir kaplama X birleşimi X ile çakışıyorsa S kapağına denir açık eğer her S α uzayda (X, Ω) açıksa.
Özellikle, uzayın tabanı (X, Ω) X'in açık bir örtüsüdür. Bununla birlikte, X'in her örtüsü, X üzerinde bir topolojinin tabanı olarak hizmet edemez.
Soru ortaya çıkar: eğer X'in bir kaplamasıysa, o zaman bu aile bu topolojinin temeli olacak şekilde X üzerinde bir topoloji hangi koşullar altında inşa edilebilir? Aşağıdaki teorem bu soruya cevap verir.
Teorem 1.10.
İzin vermek . Bir örtü β =, X üzerindeki bazı topolojinin bir tabanıdır, ancak ve ancak, β'dan her V α için β'dan her V β ve her x V α V β noktası için, x V olacak şekilde bir V γ β varsa γ (V α V β).
Kanıt.β = uzayın tabanı olsun (X, Ω). β Ω olduğundan, topolojik uzayın c) aksiyomu sayesinde, β koleksiyonundan herhangi iki kümenin kesişimi bir açık kümedir, yani, V α V β Ω. Dolayısıyla, Teorem 1.9'a göre, herhangi bir х V α V β noktası için, x V γ (V α V β) olacak şekilde V γ β vardır.
Tersine, örtünün β teoremin koşulunu sağlamasına izin verin. Boş bir kümeden ve β'den gelen tüm olası küme birleşimlerinden oluşan bir Ω ailesi tanımlayalım. Oluşturulan Ω ailesinin bir topolojik uzayın a) - c) aksiyomlarını sağladığını gösterelim. Aksiyom a) açıktır: boş küme hipotez yoluyla Ω'a girer ve küme, β'dan gelen tüm kümelerin birleşimi olarak Ω'a aittir. b) aksiyomunu kontrol edelim. J'den herhangi bir α indeksi için U α Ω olan bir kümeler ailesi olsun. Her U α kümesi, β'den bazı kümeler koleksiyonunun birleşimidir: burada V α, γ β her α J indeksi ve her bir γ G indeksi için. Sonra, yani... küme, β'dan bazı küme koleksiyonlarının birleşimidir ve bu nedenle, Ω ailesine aittir. Aksiyom c)'yi doğrulamak için, herhangi iki U kümesinin Ω'dan kesişimini göstermek yeterlidir. Ω'a aittir. U kümelerini aşağıdaki biçimde temsil ediyoruz: burada her γ G için V γ β, her δ D için δ β. Kesişmeyi düşünün. İlk olarak, V γ δ formunun her kümesinin Ω'a ait olduğundan emin olalım. Gerçekten de, herhangi bir x V γ δ noktası için, teoremin hipotezine göre, x W x V γ δ olacak şekilde bir W x β kümesi vardır. Bu nedenle, V γ δ = kümesi. Elde edilen eşitlik, V γ δ Ω kümesinin, β koleksiyonundaki bazı küme ailelerinin birleşimi olduğunu göstermektedir. Bu nedenle, U kümesi, Ω'a ve dolayısıyla b), U Ω aksiyomuna ait bazı kümeler ailesinin birleşimidir. Böylece, Ω ailesi, bir topolojik uzayın a) - c) aksiyomlarını karşılar, yani, X üzerinde bir topolojidir ve β kaplaması tanım gereği Ω için bir tabandır.
Teorem kanıtlanmıştır.
Teorem 1.10'un ispatında, eğer teoremin koşullarını karşılayan bir kaplama β verilirse, X üzerinde bir topoloji oluşturmak için bir yöntemin belirtildiğine dikkat edin.
İsteğe bağlı bir kapsama alanı verilirse X üzerinde bir topoloji oluşturmak mümkün müdür? Bu sorunun cevabı aşağıdaki teorem ile verilmektedir.
Teorem 1.11.
X kümesinin keyfi bir kaplaması olsun. O zaman S'den gelen tüm olası sonlu eleman kesişimlerinin ailesi, X üzerindeki bazı topolojinin tabanını oluşturur.
Kanıt. K'nin I'nin keyfi bir sonlu alt kümesi olduğu örtünün temel kriteri sağladığını doğrulayalım. β ailesinin herhangi iki öğesinin kesişiminin yine β ailesinin bir öğesi olduğunu fark ederek, Teorem 1.10'u uygularız: β'ya ait herhangi bir U α, V β kümesi için V γ = V α V β koyarız. O zaman S'den sonlu sayıda kümenin kesişimi olarak V γ β. Sonuç olarak, herhangi bir х V α V β noktası için: х V γ = (V α V β) elde ederiz. Böylece, Teorem 1.10'a göre β, X üzerindeki bazı topolojilerin bir tabanıdır.
Teorem kanıtlanmıştır.
Uzayın (X, Ω) açık alt kümelerinin γ ailesine denir. temel topolojiΩ ailesi, γ'den kümelerin olası tüm sonlu kesişimlerinden oluşan β ailesi, Ω topolojisinin tabanını oluşturur.
Teorem 1.11, bir X kümesinin her kapağının, X üzerindeki bazı topolojinin bir ön temeli olduğunu iddia eder.
Açıkçası, bir uzayın her tabanı aynı zamanda onun ön tabanıdır. Tipik olarak, bir topolojinin birçok tabanı ve ön tabanı vardır. Çözülmekte olan probleme bağlı olarak bunlardan biri veya diğeri tercih edilebilir.
ders çalışması
konuyla ilgili: "Genel topolojinin unsurları"
Tanıtım
Topoloji, geometrinin en genç dallarından biridir. Topoloji, modern matematiğin en soyut alanlarından biridir. Yaklaşık yüz yıllık varlığı boyunca matematiğin birçok dalı için önemli sonuçlar elde etmiştir.
Topoloji (Yunanca "τοποξ" - yer, mahalle, "λογοξ" - yasadan) süreklilik fikirlerini inceleyen bir matematik dalıdır. Topolojide, çizgi ve yüzey gibi temel geometri kavramlarının kesin tanımları ilk kez verilmektedir. Topolojinin konusu, homeomorfizmalar altında korunan, yani bire bir ve her iki yönde de sürekli olan şekillerin özellikleridir. Bir bilim olarak topoloji, matematiksel analizle ilgili ihtiyaçlardan doğmuştur. Bu bilim, genç olarak kabul edilmesine rağmen, tam olarak matematiksel analizle olan yakın bağları nedeniyle uzun süredir bilinmektedir. Topoloji fikirleri, 19. yüzyılın önde gelen matematikçilerinin eserlerinden gelmektedir. Rimman, Poincare, Cantor, Euler gibi. Topolojinin gelişimi hızlı bir tempoda ve çok sayıda yönde ilerliyor, topolojinin karşı karşıya olduğu bir dizi büyük problem başarıyla çözülmüş olsa da, bu süreç şu anda bitmedi. Topolojik yöntemler, matematiksel araştırmalar için güçlü bir araç haline geldi. Topolojik yaklaşım, klasik matematiğin temel teoremlerinin birçok ispatını basitleştirmeyi ve bu teoremleri daha geniş uzay sınıflarına genelleştirmeyi mümkün kılar.
Okul dersinin geometrisi, esas olarak uzunluk, alan, hacim kavramlarıyla ilişkili şekillerin özellikleri, yani şekillerin metrik özellikleri ile ilgilidir. Okul geometri dersinin sadece çok az teorem ve problemi farklı nitelikteki özellikleri dikkate alır. Topoloji, tam olarak, nicelikleri ölçmeden ve karşılaştırmadan oluşturulabilen, ancak aynı zamanda geometrik bir anlama sahip olan şekillerin özelliklerini inceleyen geometri dalıdır.
Ders çalışmasının ilk bölümünün amacı, genel topolojinin ana unsurlarını ele almaktı.
· Bir topolojik uzayın tanımını verin;
· Topolojik uzayların özelliklerini göz önünde bulundurun;
· Topolojik dönüşümleri karakterize etmek.
Bu çalışmanın ikinci bölümünde yüzeylerin topolojik özelliklerini ele almaya çalıştık. Aşağıdaki görevler belirlendi:
· İki boyutlu manifoldun bir tanımını verin;
· Yüzeyin Euler özelliklerini göz önünde bulundurun;
· Yönlendirilmiş ve yönlendirilmemiş yüzeyleri karakterize etmek.
1. Genel topolojinin unsurları
1.1 Bir topolojik uzay kavramı
1.1.1 Metrik uzay kavramı
Tanım 1. A ve B kümelerinin Kartezyen çarpımı, tüm sıralı çiftlerin (x, y) kümesi olarak tanımlanır; burada xÎA, yÎB, yani
A´B = ((x, y) | xÎA, yÎB).
Özellikle, A = B mümkündür.
Tanım 2. Bir eşleme tanımlanmışsa, bir X kümesinde bir r metriğinin verildiğini söylüyorlar.
r: X ´ X®R,
aşağıdaki aksiyomların karşılanması:
1. "x, y Î X (r (x, y) ³ 0) ve r (x, y) = 0 Û x = y."
2. "x, y Î X (r (x, y) = r (y, x))).
3. "x, y, zÎ X (r (x, y) + r (y, z) ³r (x, z))).
Koşul 1, 2, 3 metrik aksiyom olarak adlandırılırken, koşul 2 simetri aksiyomu ve 3 ise üçgen aksiyomu olarak adlandırılır.
Tanım 3.Üzerinde belirli bir r metriği bulunan X kümesine metrik uzay denir ve (X, r) ile gösterilir.
Hangi metrikten bahsettiğimizin açık olduğu durumlarda, metrik uzay (X, r) basitçe X ile gösterilir.
r (x, y) sayısına X uzayında x ve y noktaları arasındaki uzaklık denir.
1.1.2 Metrik uzay örnekleri
örnek 1... Rasgele boş olmayan bir X kümesinin elemanlarının uzaklığını aşağıdaki gibi tanımlarız:
.Açıkça, 1 - 3 aksiyomları sağlanır ve bu nedenle (X, r) bir metrik uzaydır.
Örnek 2 ... Uzaklık ile gerçek sayılar kümesi R
r (x, y) = (y - x) 2 bir metrik uzay değil.
Gerçekten de, üçüncü aksiyom tutmaz. Örneğin, 2, 3 ve 4 numaralı üç nokta için şunu elde ederiz:
r (2, 3) = (3 - 2) 2 = 1, r (3, 4) = (4 - 3) 2 = 1,
r (2, 4) = (4 - 2) 2 = 4 ve r (2, 3) + r (3, 4)< r(2, 4).
Tanım 1.(X, r) bir metrik uzay olsun, x 0 Î X,
r> 0 gerçek bir sayıdır. Merkezi x 0 ve yarıçapı r olan açık bir top küme olarak adlandırılır.
U (x 0, r) = (x | xÎX, r (x, x 0) Tanım 2. GÌ X alt kümesi açık olarak adlandırılacaktır. (X, r) noktalarından herhangi biri G'de bulunan bir açık topun merkeziyse. Boş küme Æ da açık küme olarak kabul edilir. Tanım 3. Bu noktayı içeren herhangi bir açık kümeye Ametrik uzaydaki bir noktanın komşuluğu denir. (X, r)'deki tüm açık kümelerin koleksiyonunu basitçe Ф r ile gösterelim. O halde aşağıdaki teorem geçerlidir. Teorem. 1) Ф r'den kümelerin herhangi bir koleksiyonunun (G a) birleşimi Ф r'ye aittir. 2) Ф r'den herhangi iki G 1 ve G 2 kümesinin kesişimi Ф r'ye aittir. G 1 ÇG 2 Î Ф r. 3) X metrik uzayı bir açık kümedir, yani, X Î Ф r, ÆÎ Ф r. Kanıt. 1) İzin ver Rastgele bir x 0 ÎG noktası alın. O zaman x 0 Î olacak şekilde bir 0 vardır. U (x 0, r 0) Ì O halde G bir açık kümedir. 2) G = G 1 ÇG 2 olsun, burada G 1, G 2 Î Ф r ve G x 0 ÎG ise, x 0 ÎG 1 ve x 0 ÎG 2. O zaman öyle bir yarıçap vardır ki r 1 ve r 2 U (x 0, r 1) ÌG 1, U (x 0, r 2) ÌG 2. r = min (r 1, r 2) gösteririz, o zaman U (x 0, r) ÌG 1 ÇG 2 = G. O halde G bir açık kümedir. 3. Her zaman hayal edebileceğiniz gibi burada U a, nokta merkezli r yarıçaplı açık bir top Aşağıda, metrik uzaydaki (X, r) tüm açık kümelerin tanımlanan Ф r ailesi, X'deki r metriği tarafından indüklenen topoloji olarak adlandırılacaktır. 1.1.3 Topolojik uzayların tanımı ve örnekleri Metrik uzaylar teorisinin birçok kavramı (limit, limit noktası, temas noktası, kümenin kapanması, kümenin sınırı, süreklilik vb.) komşuluk kavramına veya aynısı olan açık küme kavramı. Komşuluk ve açık küme, metrikler kullanılarak tanımlanır. Metrik uzaydaki açık kümelerin özellikleri aksiyom olarak alınır. Bu yol bizi, metrik uzayların özel bir durum olduğu topolojik uzaylara götürür. Tanım 1. X, keyfi nitelikteki boş olmayan bir öğeler kümesi olsun, Ф = ( 1. X kümesinin kendisi ve boş Æ kümesi F ailesine aittir. 2. Φ'den herhangi bir küme ailesinin birleşimi de F'ye aittir. 3. Φ kümesinden herhangi iki kümenin kesişimi de F kümesine aittir. Daha sonra Φ ailesine topoloji veya topolojik yapı denir. Bir çift (X, Ф) veya başka bir deyişle, belirli bir topolojinin verildiği bir X kümesine topolojik uzay denir. X kümesinin öğelerine topolojik uzayın noktaları, Φ ailesinin öğelerine (X, Φ)'deki açık kümeler denir. Yanlış anlaşılmalar söz konusu olmadığında, basitçe şunu yazmasına izin verilir: X bir topolojik uzaydır, G Topolojik uzaylara örnekler. Örnek 1. X keyfi bir kümedir. Bir topolojik uzayın 1. aksiyomu, X'teki herhangi bir topolojik yapının açık kümeleri arasında boş bir Æ kümesi ve X kümesinin kendisinin olması gerektiğini ima eder. Ф т = (Æ, X), sadece bu iki kümeden oluşan aksiyom 2 ve 3 de geçerlidir. Bu nedenle, Φ m = (Æ, X), X'teki en basit topolojik yapıdır. Bu topolojiye önemsiz denir ve (X, Φ) çiftine önemsiz bir topolojik uzay denir. Bu çifte bazen antidiscrete topolojik uzay denir. Örnek 2. Diğer uç nokta ise ayrık topolojik uzaydır (X, Φ d), burada Φ d, X kümesinin tüm alt kümelerinin ailesidir. Açıkçası, bu durumda, tüm aksiyomlar 1 - 3 karşılanır. Bu kavramların doğası tarafından belirlenen doğal genellik düzeyinde süreklilik ve sınıra geçiş çalışmasına ayrılmış geometri dalı. O. t.'nin ilk kavramları, kavramlardır. topolojik uzay ve sürekli ekran, 1914 yılında F. Hausdorf tarafından tahsis edilmiştir. Sürekli eşlemelerin özel bir durumu, homeomorfizmler, topolojik sürekli karşılıklı özdeş eşlemelerdir. sürekli ters eşlemeli uzaylar. Bir homeomorfizm (yani, homeomorfik uzaylar) vasıtasıyla birbirine haritalanabilen uzayların, bir optik uzayda aynı olduğu varsayılır. Optik teorinin ana görevlerinden biri, doğal topolojik nesnelerin seçimi ve incelenmesidir. değişmezler, homeomorfizmalar tarafından korunan uzayların bir özelliğidir. Elbette, bir uzayın formüle edilen her özelliği hariç tutulur. topolojisi açısından, otomatik olarak topolojiktir. değişmez. Kanıt topolojiktir. uzayın özelliğinin değişmezliği, yalnızca uzay noktaları kümesinde tanımlanan herhangi bir ek yapının dahil edilmesiyle ve topolojisiyle şu veya bu şekilde ilgili olarak formüle edildiğinde gereklidir. Bir örnek topolojiktir. homoloji gruplarının değişmezliği. Topolojik değişmez mutlaka bir sayı değildir; örneğin, bağlanabilirlik, kompaktlık, ölçülebilirlik - topolojik. değişmezler. Sayısal değişmezler arasında (belirli topolojik uzaylarda sayısal değerler alarak), en önemlileri boyut değişmezleridir: küçük endüktif boyut ind, büyük endüktif boyut Ind ve Lebesgue boyut dim (kaplama anlamında boyut). Önemli bir rol topolojik tarafından oynanır. değerleri olan farklı nitelikteki değişmezler Kardinal sayılar. Aralarında: ağırlık, karakter. Topolojik sistemle bağlantılı olarak. değişmezler topolojik sınıfları ortaya çıkarır. boşluklar - her sınıf, bir veya başka bir topolojik kısıtlama ile belirlenir. in-varyasyon. En önemli sınıflar metriklenebilir uzaylar, bikompakt uzaylar, Tikhonov uzayları, parakompakt uzaylar, cirrus uzayları. Optik teorinin ana "iç" sorunları şunlardır: 1) yeni önemli topolojik sınıfların tanımlanması. boşluklar; 2) farklı topolojik sınıfların karşılaştırılması. boşluklar; 3) belirli bir sınıf içindeki uzayların ve bu sınıfın bir bütün olarak kategorik özelliklerinin incelenmesi. Bu grubun merkezi, elbette, O. t'nin iç birliğini sağlamayı amaçlayan görev 2)'dir. Yeni önemli topolojik sınıfların tahsisi. uzaylar (yani, yeni topolojik değişmezler) genellikle bir uzaydaki (sayısal, cebirsel, sıralı) ek yapıların, topolojisiyle doğal olarak tutarlı olmasıyla ilişkilendirilir. Böylece metriklenebilir uzaylar, sıralı uzaylar, topolojik grupların uzayları ayırt edilir. simetrik uzaylar vb. 1), 2), 3) problemlerinin çözümünde önemli bir rol kaplama yöntemi ile oynanır. En önemlileri yazılı ve yıldız yazılı ilişkileri olan kaplamalar ve kaplamalar arasındaki ilişkiler dilinde, bicompact ve paracompact uzayların temel sınıfları ayırt edilir ve tenyolojik formüle edilir. kompaktlık tipinin özellikleri. Kaplama yöntemi önemli bir rol oynar. teorinin pas boyutluluğu. Merkezi problemi 2) çözmek için, uzayların ve eşlemelerin karşılıklı sınıflandırılması yöntemi özellikle önemlidir. Farklı topolojik sınıflar arasında bağlantılar kurmayı amaçlar. boşluklar, bir veya daha fazla basit kısıtlamaya tabi olan sürekli eşlemeler aracılığıyla. Çok genel nitelikteki uzaylar, burada "iyi" eşlemeler altındaki daha basit uzayların görüntüleri olarak tanımlanabilir. Örneğin, ilk sayılabilirlik aksiyomuna sahip uzaylar, metriklerin görüntüleri olarak karakterize edilir. sürekli açık eşlemeler altındaki boşluklar. Bu tür bağlantılar, topolojik sınıflar düşünüldüğünde etkili bir referans noktaları sistemi oluşturur. boşluklar. Ters yöntem spektrum, kaplama yöntemi ve haritalama yöntemi ile yakından ilgili, karmaşık topolojik çalışmayı azaltmanıza izin verir. uzaylar daha basit olan uzay haritalarının sistemlerini dikkate alır. Son olarak, problem 2) çözümünde, kardinal değerli topolojik yöntem değişmezler veya güç özellikleri. Bu tür değişmezler, O. t'nin küme-teorik doğasıyla en uyumludur. Bu bağlamda, kardinal değerli değişmezler sistemi oldukça dallıdır ve pratik olarak tüm diğer topolojik üzerinde bir etkiye sahiptir. özellikler. Kardinal değerli değişmezlerin bir diğer önemli özelliği, bu değişmezler üzerinde aritmetik gerçekleştirme yeteneğine dayanan yakın ilişkileridir. işlemleri ve büyüklüklerini karşılaştırın. Bu özellikleri nedeniyle, temel değerli değişmezler teorisi, teori teorisinde birleştirici bir rol oynar ve bölümlerinin herhangi birine bir yaklaşım sağlar. Optik teorinin dış problemleri arasında, genel bir doğaya sahip şu problem öne çıkıyor: topolojinin ve bu topoloji ile tutarlı diğer yapıların özellikleri nasıl ilişkilidir ve etkileşim içindedir? Bu tür somut problemler topolojik gruplar, topolojik vektör uzayları ve topolojik uzaylar üzerindeki ölçülerle ilgilidir. Her bicompactum'a karşılık gelen banach cebiri Bu kompakt uzaydaki tüm sürekli gerçek fonksiyonların Bu teori topolojiktir. uzaylar, Banach cebirleri teorisi ile yakından ilişkilidir. Fonksiyonel analizde önemli bir rol şu şekilde oynanır: zayıf topolojiler Banach uzaylarında. Bu, uygulamalar için ölçülemeyen topolojilerin önemli bir sınıfıdır. Her Tikhonov uzayı, noktasal yakınsama topolojisinde, üzerindeki tüm sürekli gerçek fonksiyonların halkası ile benzersiz bir şekilde karakterize edilir. Bu tür sonuçlar O. t.'ye bağlanır ve topolojik cebir. konsept bikompakt uzantı potansiyel teoride uygulama buldu ( Çevre sınırı, Martina sınırı).
O. t. Metodik olarak önemlidir. matematik öğretirken tutum. Süreklilik, yakınsama, paralel geçiş gibi temel kavramlar ancak kendi kavramları ve yapıları çerçevesinde tam olarak açıklığa kavuşturulmuş ve şeffaftır. Teori teorisinin kavramlarının ve dilinin hiç kullanılmadığı matematik alanlarını adlandırmak zordur. Bu, özellikle matematikteki birleştirici rolünü ortaya koymaktadır. t teorisinin matematikteki konumu da genel matematiksel bir takım ilke ve teoremlerin olması gerçeğiyle belirlenir. anlam, doğal (yani, bu ilkelerin, teoremlerin doğasına karşılık gelen) formülasyonunu yalnızca genel bir teori çerçevesinde kazanır. Örnekler, kompaktlık kavramıdır - sonlu bir alt örtünün seçimine ilişkin Heine - Borel lemmasından bir soyutlama bir aralığın, kompakt uzayların bir ürününün kompaktlığı üzerine teorem (bunun arkasında, bir ön görüntü olarak, sonlu boyutlu bir küpün kompaktlığı hakkındaki iddia), bir kompakt uzayda sürekli bir gerçek fonksiyonun sınırlı olduğu teoremi maksimum ve minimum değerlerine ulaşır. Bu örnek dizisi devam ettirilebilir: ikinci kategorideki bir küme kavramı, tamlık kavramı, uzam kavramı (bir bütün olarak matematik için önemli olan bu kavramların doğası ve bunlarla ilgili sonuçlar, OT çerçevesinde çalışmalarını en doğal ve şeffaf hale getirir). Aydınlatılmış.: Aleksandrov PS, Gerçek değişkenli fonksiyonlar teorisi ve topolojik uzaylar teorisi, Moskova, 1978, s. 280-358; onu, "Uspekhi Matem. Nauk", 1960, cilt 15, c. 2, s. 25-95; onunla aynı yerde, 1964, c. 19, c. 6, s. 3-46; 1965, cilt 20, c. 1, s. 253-54; Aleksndrov P.S, Fedorchuk V.V., age, 1978, cilt 33, yüzyıl. 3, s. 3- 48; Arkhangelsky A.V., age, 1966, t. 21, yüzyıl. 4, s. 133-84; him, age, 1978, cilt 33, c. 6, s. 29-84. Fiziksel ansiklopedi matematik ansiklopedisi matematik ansiklopedisi Modern Doğa Biliminin Başlangıçları Doğal bilim. ansiklopedik sözlük Büyük Sovyet Ansiklopedisi Collier'in Ansiklopedisi Büyük ansiklopedik sözlük Rus dilinin yazım sözlüğü Ushakov'un Açıklayıcı Sözlüğü Efremova'nın Açıklayıcı Sözlüğü Yazım sözlüğü referansı Rusça yazım sözlüğü Rus dilinin yabancı kelimeler sözlüğü Kelime formları eşanlamlı sözlük Leonardo'nun Topolojisi Üstadın günlüklerini inceledikten sonra araştırmacılar, topoloji gibi bir bilimin kökeninde Leonardo olduğunu güvenle söyleyebilirler.Topoloji, çalışmayı en genel biçimde ele alan bir matematik dalıdır. fenomen Bölüm 2. Kuantum kronotopunun topolojisi “Uzay-zaman fiziğinde yanlış öncüllere sahip koşullu ifadelerin (" Faraday 1830'da öldüyse ... ") mantıklı olmadığı sonucuna varmak zorunda kalıyoruz. Mantıkçılar bu tür ifadelere koşullu, çelişkili gerçekler ve Ticari Topoloji Bölümümüzde, Mobius'un kendisinin imreneceği topolojik süreçler gelişiyordu.Hastanede çalışmaya başladığımda, Sayman tarafından yönetilen hemşirelik liderliği, departmandaki gücü çoktan ele geçirmişti. Kadife bir devrimdi çünkü BİR GÜLÜMSEMENİN TOPOLOJİSİ Yüzyıldan önce doğmuş bir genç şimdi doğuyor! Mikhail Kuzmin Söylenti doğrudan devamını seste buluyor. Dahası. Kulaklara kadar uzanan salyangoz dudakları bir gülümseme oluşturur. Basitçe "ağızdan kulağa" denir ve şiirsel olarak - "Doğum 1.9. Tat Topolojisi 1.9.1. Kulüp Tavsiyeleri ve Okuma Sevgisi İşbirliğine dayalı filtrelemeden doğan çeşitli uygulamaları ve kurumları analiz ederken, bunların sağlam temeller üzerine inşa edildiğinden emin olmanın zararı olmaz. Bu yüzden görmezden gelmeye hakkımız yok. GEÇMİŞİN TOPOLOJİSİ Bu, geçmişi anlama çabamızdaki ikinci kitabımız. Masonluğun kökenleri hakkında mümkün olduğunca çok şey öğrenmeyi umarak araştırmamıza temiz bir kağıtla başladık. Ancak yavaş yavaş çalışmamız daha geniş alanları kapsadı ve daha uzun sürdü, yazar Ağ topolojisi Bir ağ oluşturmaya başlamadan önce, bağlanacak bilgisayarların nerede ve nasıl bulunacağını bulmanız gerekir. Ayrıca gerekli ağ ekipmanının yerini ve bilgisayarları birbirine bağlayan kabloların nasıl çalışacağını belirlemek gerekir. Bir kelimeyle, Ortak veri yolu topolojisi Bu topolojinin kısa bir tanımı, tek bir kablo üzerinden bağlanan bir dizi bilgisayardır (Şekil 12.1). Ağ, bir koaksiyel kablo temelinde inşa edilmiştir. Pirinç. 12.1. Ortak veri yolu topolojisi Bu topoloji ilkti, ancak aktif olarak Yıldız topolojisi Bu topolojide her bilgisayar kendi kablosuyla hub gibi bir ağ aygıtına bağlanır. Böyle bir bağlantı, adının geldiği bir yıldıza benziyor (Şekil 12.2). Pirinç. 12.2. Yıldız ağı Halka topolojisi Bilgisayarların bağlı olduğu kablo kapalı ise topolojiye “halka” adı verilir (Şekil 12.3). Pirinç. 12.3. "Halka" topolojisine göre oluşturulmuş bir ağ Böyle bir bağlantı ile, her bilgisayar ortaya çıkan sinyali daha önce bir daire içinde iletmelidir. Birleşik topoloji Birleşik topoloji, yukarıdaki topolojilerden biri diğeriyle kesiştiğinde oluşur (Şekil 12.4). Pirinç. 12.4. Ağ bağlayan yıldız ve ortak veri yolu topolojileri Bu tür topolojilerin örnekleri aşağıdakileri içerir. Sanmak Fiziksel topoloji Bir PKI sistemi, sertifika verme, anahtar oluşturma, güvenliği yönetme, kimlik doğrulama ve verileri kurtarma gibi bir dizi işlevi gerçekleştirmenin yanı sıra, harici sistemlerle entegrasyon sağlamalıdır. PKI ile etkileşime girmesi gerekiyor Standart veya Gelişmiş lisans ile kullanılabilir. Topoloji, düzenleme araçları ve teknolojileriyle birlikte bir coğrafi veritabanındaki geometrik ilişkileri daha doğru bir şekilde modellemenize olanak tanıyan bir kurallar dizisidir. ArcGIS'te topoloji, özelliklerin coğrafi alanda kendi kendine nasıl konumlandırılacağını tanımlayan bir dizi kural ve aynı şekilde paylaşılan geometriye sahip unsurlara uygulanan bir dizi düzenleme aracı aracılığıyla sağlanır. Topoloji, bir veya daha fazla özellik sınıfındaki özelliklerin geometriyi nasıl paylaştığını tanımlayan bir veya daha fazla ilişki olarak bir coğrafi veritabanında depolanır. Topolojiye katılan özellikler basit özellik sınıfları olarak sınıflandırılır - topoloji bir özellik sınıfının tanımını değiştirmez, daha ziyade bu özelliklerin uzamsal ilişkilerini tanımlar. Uzun bir süredir topoloji, verileri yönetmek ve bütünlüğünü kontrol etmek için CBS'nin önemli bir unsuru olmuştur. Genel olarak, topolojik veri modeli, uzamsal nesneleri (nokta, çizgi ve alan nesneleri) şematik topolojik ilkeller - düğümler, yüzler ve kenarlar biçiminde temsil ederek uzamsal ilişkileri yönetir. Bu ilkeller, aralarındaki ve sınırlarını temsil ettikleri nesnelerle olan ilişki, topolojik elemanların bir grafiğindeki özelliklerin geometrisinin haritalanmasıyla belirlenir. Topoloji, öncelikle uzamsal ilişkilere sahip verilerin kalite kontrolü için kullanılır ve ayrıca derlemeye yardımcı olur. Çoğu durumda, topoloji aynı zamanda uzamsal ilişkileri analiz etmek için de kullanılır - örneğin, aynı öznitelik değerine sahip olan bitişik çokgenler arasındaki sınırları kaldırmak veya bir topolojik grafik öğeleri ağı boyunca bir yol döşemek için. Topoloji ayrıca birkaç farklı özellik sınıfı arasında geometri entegrasyonunu modellemek için kullanılır. Bu bazen özellik sınıflarının dikey entegrasyonu olarak adlandırılır. Özellikler bir topoloji içinde geometriyi paylaşabilir. Aşağıdakiler bitişik özelliklere örneklerdir: Ayrıca, paylaşılan geometri, coğrafi veritabanı topolojisi kullanılarak özellik sınıfları arasında paylaşılabilir. Örneğin: Parseller, parselleri, sınırları, köşe noktalarını ve kontrol noktalarını modellemek için gereken özellik sınıfları kümesi, eşleşen kuralları izlediğinden, parseller genellikle basit özellik sınıfları ve coğrafi veritabanı topolojisi kullanılarak yönetilir. Paketleri yönetmenin başka bir yolu da bu katmanları otomatik olarak sağlayan bir paket veri kümesi kullanmaktır. Parsel veri kümesi kendi iç topolojisini yönetir, bu nedenle coğrafi veri tabanı topolojisini korumaya veya parseller tarafından kullanılan katmanlar üzerinde herhangi bir topolojik düzenleme gerçekleştirmeye gerek yoktur. Basit özellikler olarak modellenen parseller ile bir parsel veri setindeki parseller arasındaki temel fark, parsel sınırlarının (parsel veri setindeki çizgiler) parsel veri setinde paylaşılmamasıdır — her parsel tam bir sınır çizgisi seti içerir; bitişik parsel hatları örtüşür ve birbiriyle örtüşür. Ancak parsel veri kümeleri bir coğrafi veritabanı topolojisine katılabilir; orada, örtüşen sınır çizgileri farklı geometrilere sahiptir, çizgiler ayrılır ve topoloji grafiği her zamanki gibi oluşturulur. Bir çokgen katmanı tanımlanabilir ve kullanılabilir: Bu, uzamsal nesnelerle çalışmak için iki seçenek olduğu anlamına gelir: bir durumda, koordinatları verilmiş uzamsal nesnelerle çalışırsınız ve diğerinde, topolojik öğelerin sıralı bir grafiği olarak temsil edilen nesnelerle çalışırsınız. Geodatabase topolojisi ile çalışmak için bu bölümü okumak gerekli değildir. Ancak, coğrafi veritabanlarında topolojinin tarihi ve evrimi ile ilgileniyorsanız bu bölümü okuyun. ArcInfo Workstation kaplamaları uzun bir kullanım geçmişine sahiptir ve verilerin mekansal bütünlüğünü sağlamak için topolojinin önemini göstermiştir. Kapsama veri modeli aşağıdaki unsurları içerir. Özellik sınırları ve kapsamadaki noktalar, ArcInfo Workstation tarafından yönetilen birkaç çekirdek dosyada saklandı. "ARC" dosyası, "yaylar" adı verilen topolojik kenarlar biçiminde çizgi veya çokgen sınır geometrisi içeriyordu. LAB dosyası, çokgen çizmek için başlangıç noktaları olarak veya kuyular gibi ayrı nokta özellikleri olarak kullanılan nokta özelliklerini içeriyordu. Çokgen kenarları arasındaki topolojik ilişkileri tanımlamak ve sürdürmek için başka dosyalar kullanıldı. Örneğin, "PAL" dosyası ("Poligon-yay listesi"), her bir çokgenin yaylarının sırasını ve yönünü içeriyordu. ArcInfo Workstation'da programlı mantık kullanılarak, verileri görüntülemek, analiz etmek ve sorgulamak amacıyla her bir çokgenin koordinatları birleştirildi. PAL dosyasında bulunan sıralı liste, ARC dosyasında saklanan kenar koordinatlarını bulmak ve birleştirmek için kullanıldı. Çokgenler, çalışma sırasında gerektiği gibi monte edildi. Kaplama modelinin çeşitli avantajları vardı: İlginç bir tarihsel gerçek: Arc'ın Bilgi tablosu yöneticisi ile birleşimi, Esri ürün ailesindeki tüm sonraki Arc ürünlerinin evrimleştiği ArcInfo Workstation ürün adını doğurdu - ArcInfo, ArcIMS, ArcGIS, vb. Kaplamaların ayrıca birkaç dezavantajı vardı: 1980'lerin başında, kaplamalar, çokgenlerin kapalı döngüler olarak depolandığı eski çokgen ve çizgi sistemleri üzerinde önemli bir gelişme olarak görülüyordu. Bu eski sistemlerde, unsurların tüm koordinatları, bu unsurların geometrisi ile birlikte saklandı. Kapsama ve ArcInfo Workstation'ın ortaya çıkmasından önce, bu basit çokgen ve çizgi yapıları kullanılıyordu. Bu veri yapısı basitti, ancak "çift sayısallaştırılmış sınırların" önemli bir dezavantajı vardı. Onlar. ortak yüzleri olan her çokgenin geometrisinde, bitişik parseller için koordinatların iki kopyası saklandı. Ana dezavantaj, o sırada CBS yazılımının paylaşılan kenarların bütünlüğünü yönetememesiydi. Ayrıca, bilgi depolamanın maliyeti çok yüksekti, her bir baytın kaydedilmesi gerekiyordu. 1980'lerin başında, 300 MB'lık bir sabit disk, çamaşır makinesi boyutundaydı ve 30.000 dolara mal oluyordu. İki veya daha fazla koordinat setini saklamak pahalıydı ve hesaplamalar çok fazla makine zamanını aldı. Bu nedenle, bir kapsama topolojisi kullanmanın gerçek faydaları vardı. 1990'ların ortalarında, disk alanı maliyeti düştükçe ve bilgi işlem gücü arttıkça basit geometrik yapılara olan ilgi arttı. Aynı zamanda, CBS veri kümeleri giderek daha erişilebilir hale geldi ve CBS kullanıcıları, birincil veri derlemesinden veri işleme ve analizine geçmeye başladı. Kullanıcılar verilerle çalışırken performansı artırmak istediler (örneğin, şu anda gerekli olan çokgenin geometrisinin hesaplanmasını beklemek değil, yalnızca çokgenlerin koordinatlarını olabildiğince çabuk almak). Unsurların tam geometrisinin kullanılabilirliğinin daha verimli olduğu bulundu. Binlerce GIS kullanıcısı çok sayıda kullanılabilir veri seti oluşturmuştur. Esri, bu süre zarfında şekil dosyası biçimini geliştirdi ve yayınladı. Shapefiles, özelliklerin koordinatlarını saklamak için çok basit bir model kullandı. Her şekil dosyası bir özellik sınıfını (nokta, çizgi veya çokgen) temsil ediyordu ve özelliklerin koordinatları için basit bir depolama modeli kullandı. Şekil dosyaları, kapsamlardan ve diğer CBS formatlarından kolayca oluşturuldu. Hızla fiili format haline geldiler, yaygınlaştılar ve bugün hala kullanılıyorlar. Birkaç yıl sonra ArcSDE, verileri ilişkisel veritabanı tablolarında depolamak için basit bir model önerdi. Bir özellik tablosu, geometrisi ve nitelikleri hakkında bilgilerle birlikte tek bir özelliği bir dize olarak saklayabilir. Durum çokgenlerini içeren böyle bir tablonun bir örneği aşağıda gösterilmiştir. Her satır bir durumu temsil eder. Şekil sütunu, her durum için çokgen geometrisini içerir. Bu basit özellik modeli, SQL işleme motoruna çok uygundur. İlişkisel veritabanları kullanılarak veri hacmindeki ve kullanıcı sayısındaki artış performans düşüşüne yol açmamıştır. CBS verilerini yönetmek için RDBMS kullanmaya başladık. Şekil dosyaları her yerde bulunur hale geldi ve ArcSDE sayesinde bu basit geometri depolama motoru, RDBMS'lerdeki özellikler için ana depolama modeli haline geldi. (Verilerin birlikte çalışabilirliğini sağlamak amacıyla Esri, OGC ve ISO basit geometri spesifikasyonunun oluşturulmasında lider bir rol üstlendi.) Basit nesneleri saklamanın belirgin avantajları vardı: Dezavantajlarından biri, basit nesnelerle çalışırken veri bütünlüğünü korumak için topolojiyi kullanamamasıydı. Sonuç olarak, kullanıcılar düzenleme ve depolama (kapsam) için bir veri modeli ve işleme için başka bir veri modeli (şekil dosyaları veya ArcSDE katmanları) kullandılar. Kullanıcılar, verileri düzenlemek ve çalışmak için bu hibrit yaklaşımı benimsemeye başladı. Örneğin, kullanıcılar kapsamlardaki, CAD dosyalarındaki veya diğer formatlardaki verileri düzenleyebilir. Ardından, haritalama kullanımı için verileri şekil dosyalarına dönüştürebilirler. Böylece, basit nesnelerin yapısı doğrudan kullanım için uygun bir format haline gelse de, paylaşılan geometrinin topolojik düzenlemesini ve yönetimini desteklemedi. Doğrudan veritabanları basit bir yapı kullanabilirdi, ancak düzenleme için farklı bir topolojik form kullanıldı. Bu, verilerle çalışırken faydalı oldu. Ancak aynı zamanda veriler güncelliğini yitirdi, güncellenmeleri gerekiyordu. Bu şema işe yaradı, ancak bilgilerin güncellenmesinde bir gecikme oldu. Sonuç olarak - topoloji yok. GIS, basit özellik geometrisi kullanan ve topolojinin bu veri yapısıyla birlikte kullanılmasına izin veren bir özellik depolama motoru gerektiriyordu. Bu, kullanıcıların nihayet her iki yaklaşımın avantajlarını birleştirebilecekleri anlamına geliyordu - topoloji sorgularına, birlikte yazmaya ve veri bütünlüğü kontrolüne izin veren işlemsel bir veri modeli ve basit geometriye dayalı basit, yüksek düzeyde ölçeklenebilir bir depolama motoru. Bu veri modelinin basit, hızlı ve verimli olduğu kanıtlanmıştır. Herhangi bir sayıda kullanıcının doğrudan düzenlenmesine ve eşzamanlı çalışmasına izin verir. Aslında, topoloji sadece bir depolama modelinden fazlasını içerir. Topoloji şunları içerir: Coğrafi veritabanı topolojisinde doğrulama süreci, özelliklerin paylaşılan koordinatlarını (hem aynı özellik sınıfı içinde hem de sınıflar arasında) belirler. Kümeleme algoritması, paylaşılan koordinatların tam olarak eşleşmesini sağlar. Paylaşılan koordinatlar, her özelliğin basit geometrisinin bir parçası olarak saklanır. Bu, topolojik özellikler (düğümler, kenarlar ve yüzler) için hızlı ve ölçeklenebilir bir arama sağlar. Ek bir avantaj, RDBMS SQL motoru ve işlem yönetimi ile çalışmaktır. Verileri düzenlerken veya güncellerken, yeni özellikler eklendikten hemen sonra kullanılabilir. Haritanın "değişen alanlar" olarak adlandırılan güncellenmiş alanları, her bir özellik sınıfında etiketlenir. Kullanıcılar istedikleri zaman topolojik analiz ve değişen alanların doğrulamasını yapabilirler. Yeniden oluşturma, yalnızca değiştirilen alanların topolojisi için gereklidir, bu da işlem süresini azaltır. Sonuç olarak, topolojik ilkeller (düğümler, kenarlar ve yüzler), aralarındaki ilişkiler ve ait oldukları özellikler hızla keşfedilebilir ve birleştirilebilir. Bu topoloji aşağıdaki avantajlara sahiptir: Kullanıcıların topolojik ilkelleri depolamayı tercih ettiği durumlarda, çeşitli analitik işlemler ve veri alışverişi için tablolar oluşturabilir ve bunlara topoloji ve bağlantılar yerleştirebilirler (örneğin, topolojik ilkellerin tablolarını depolayan Oracle Spatial'a bilgi yerleştirmek gerekirse). ). Pratik bir konu olarak, ArcGIS topoloji çözümü işe yarar. Hem veri hacmi hem de kullanıcı sayısı açısından performanstan ödün vermeden ölçeklenir. Bir coğrafi veri tabanında topoloji oluşturmak ve işlemek için çok çeşitli doğrulama ve düzenleme araçları kullanmanıza olanak tanır. Kullanıcıların hem dosya hem de ilişkisel veritabanı seviyelerinde çalışan esnek sistemler oluşturmasını ve herhangi bir sayıda şema kullanmasını sağlayan güçlü ve esnek veri modelleme araçları içerir. makalenin içeriğiKitaplarda "GENEL TOPOLOJİ"
Leonardo topolojisi
Leonardo da Vinci'nin kitabından. Bir dahinin gerçek hikayesi yazar Alferova Marianna Vladimirovna
Bölüm 2. Kuantum kronotopunun topolojisi
Grigory Perelman ve Poincaré'nin varsayımı kitabından yazar Arsenov Oleg Orestovich
ticari topoloji
Forge of Mercy kitabından yazar Smirnov Aleksey Konstantinoviç
SMİLE TOPOLOJİSİ
Osip Mandelstam'ın Dünyalar ve Çarpışmalar kitabından yazar Amelin Gregory
1.9. lezzet topolojisi
Yeni Ekonomi Manifestosu kitabından. Piyasanın ikinci görünmez eli yazar Dolgin Alexander Borisoviç
GEÇMİŞİN TOPOLOJİSİ
İkinci Mesih kitabından. Masonların büyük gizemi yazar Şövalye Christopher
Ortak veri yolu topolojisi
yazar Vatamanyuk Aleksandr İvanoviç
Yıldız topolojisi
Kitaptan Bilgisayarı kendi ellerimizle monte etmek yazar Vatamanyuk Aleksandr İvanoviç
halka topolojisi
Kitaptan Bilgisayarı kendi ellerimizle monte etmek yazar Vatamanyuk Aleksandr İvanoviç
birleşik topoloji
Kitaptan Bilgisayarı kendi ellerimizle monte etmek yazar Vatamanyuk Aleksandr İvanoviç
Fiziksel topoloji
Açık Anahtar Altyapıları kitabından yazar Polyanskaya Olga Yurievna
Topoloji neden gereklidir?
Topolojideki özellikler geometriyi nasıl paylaşır?
Not:
İki tür: topolojinin nesneleri ve öğeleri
Coğrafi veritabanı topolojisine yönelik kapsam gelişimi
Not:
"Yay düğümü" ve "jeo-ilişkisel" terimlerinin kökeni

Önceki sürümler:
Şekil dosyaları ve basit geometri depolama

ArcGIS'te topoloji çalışma alanı
TOPOLOJİ, gerilme, sıkıştırma veya bükme gibi sürekli deformasyonlar altında tutulan şekillerin (veya boşlukların) özelliklerini inceleyen bir matematik dalı. Sürekli deformasyon, kırılma (yani şeklin bütünlüğünün ihlali) veya yapıştırma (yani noktalarının tanımlanması) olmayan bir şeklin deformasyonudur. Bu geometrik özellikler, şeklin şekli veya boyutuyla değil, konumuyla ilgilidir. Öklid ve Riemann geometrileri, Lobachevsky'nin geometrisi ve uzunlukları ve açıları ölçmekle ilgili diğer geometrilerin aksine, topoloji metrik olmayan ve niteliksel bir karaktere sahiptir. Daha önce, durum analizi (konum analizi) ve nokta küme teorisi olarak adlandırılıyordu. Popüler bilim literatüründe topoloji, gerilmiş, sıkıştırılmış veya bükülmüş mükemmel elastik kauçuk levhalar üzerine çizilen şekillerin geometrisi olarak görselleştirilebildiği için genellikle "kauçuk levha geometrisi" olarak adlandırılır. Topoloji, matematiğin en yeni dallarından biridir.
Tarih.
1640'ta Fransız filozof ve matematikçi R. Descartes (1596-1650), basit çokyüzlülerin köşe, kenar ve yüzleri arasında değişmez bir ilişki buldu. Descartes bu oranı şu formülle ifade etti: V - E + F= 2, nerede V- köşe sayısı, E- kaburga sayısı ve F Yüz sayısıdır. 1752'de İsviçreli matematikçi L. Euler (1707-1783) bu formülün kesin bir kanıtını verdi. Euler'in topolojinin gelişimine bir başka katkısı da ünlü Königsberg köprüleri probleminin çözümüdür. Königsberg'deki Pregel Nehri üzerindeki bir ada (nehrin iki kola ayrıldığı yerde - Eski ve Yeni Pregel) ve adayı bankalara bağlayan yedi köprü hakkındaydı. Buradaki zorluk, her birini yalnızca bir kez ziyaret edip başlangıç noktasına geri dönen yedi köprünün tümünü kesintisiz bir rota boyunca atlamanın mümkün olup olmadığını bulmaktı. Euler, kara alanlarını noktalarla ve köprüleri çizgilerle değiştirdi. Euler, elde edilen konfigürasyona bir grafik, noktalar - köşeleri ve çizgiler - kenarlar adını verdi. Köşeleri çift veya tek sayıda kenarın köşeden ayrılıp ayrılmadığına bağlı olarak çift ve tek olarak ayırdı. Euler, bir grafiğin tüm kenarlarının, yalnızca grafik yalnızca çift köşeler içeriyorsa, sürekli kapalı bir rota boyunca tam olarak bir kez geçilebileceğini gösterdi. Königsberg köprüleri problemindeki grafik sadece tek köşeler içerdiğinden, köprüler, her birini tam olarak bir kez ziyaret ettikten ve rotanın başlangıcına geri döndüğünden, sürekli bir rota boyunca baypas edilemez.
Euler'in Königsberg köprüleri sorununa çözümü sadece köprülerin göreli konumuna bağlıdır. Matematiğin bir dalı olarak topolojinin resmi temelini attı. K. Gauss (1777-1855), daha sonra I. Listing (1808-1882), P. Tate (1831-1901) ve J. Alexander tarafından incelenen düğüm teorisini yarattı. 1840'ta A. Möbius (1790-1868), daha sonra O. de Morgan (1806-1871) ve A. Keley (1821-1895) tarafından araştırılan dört renk problemini formüle etti. Topoloji üzerine ilk sistematik çalışma, Ön Topoloji Çalışmaları Listeleme (1874).
Modern topolojinin kurucuları G. Cantor (1845-1918), A. Poincaré (1854-1912) ve L. Brauer'dir (1881-1966).
Topoloji bölümleri.
Topoloji üç alana ayrılabilir: 1) geometrik formları düzenli olarak birbirine bitişik basit şekillere bölerek inceleyen kombinatoryal topoloji; 2) grup teorisine vurgu yaparak topolojik uzaylarla ilişkili cebirsel yapıların incelenmesiyle ilgilenen cebirsel topoloji; 3) kümeleri nokta kümeleri olarak inceleyen (bir nesneyi daha basit nesnelerin birliği olarak temsil eden kombinatoryal yöntemlerin aksine) ve kümeleri açıklık, kapalılık, bağlanabilirlik vb. gibi topolojik özellikler açısından tanımlayan küme teorik topolojisi. Elbette, topolojinin bölgelere ayrılması biraz keyfidir; birçok topolog, içindeki diğer bölümleri tercih eder.
Bazı temel kavramlar.
topolojik uzay birçok noktadan oluşur S ve kümenin alt kümelerinin S koleksiyonu S aşağıdaki aksiyomların karşılanması:
(1) bütün set S ve boş küme S kümesine aittir;
(2) S'den herhangi bir küme koleksiyonunun birleşimi S'den bir kümedir;
(3) S'den herhangi bir sonlu sayıda kümenin kesişimi S'den bir kümedir.
S kümesinde bulunan kümelere denir. açık kümeler, ve bu setin kendisi - topoloji v S. Santimetre... SET TEORİSİ.
topolojik dönüşüm, veya homeomorfizm, bir geometrik şekil S başka bir, Sў, bir eşlemedir ( P ® Pў) puan P itibaren S noktalara Pў SО Aşağıdaki koşulların sağlanması: 1) Noktalar arasında kurduğu yazışmalar. S ve Sў birebirdir, yani. her nokta P itibaren S sadece bir puan eşleşir Pў Sў ve her noktaya Pў sadece bir nokta görüntülenir P; 2) eşleme karşılıklı olarak süreklidir (her iki yönde de süreklidir), yani. iki puan verilirse P, Q itibaren S ve nokta P hareket eder, böylece nokta ile nokta arasındaki mesafe Q sıfıra, ardından karşılık gelen noktalar arasındaki mesafeye eğilimlidir Pў, Qў Sў ayrıca sıfıra eğilimlidir ve bunun tersi de geçerlidir.
Topolojik dönüşümler sırasında birbirine dönüşen geometrik şekillere denir. homeomorfik... Bir karenin çemberi ve sınırı homeomorfiktir, çünkü topolojik bir dönüşümle (yani, kırmadan ve yapıştırmadan bükme ve germe, örneğin bir karenin kenarını, etrafı çevrelenmiş bir daire ile germe) ile birbirlerine dönüştürülebilirler. ). Küpün küresi ve yüzeyi de homeomorfiktir. Rakamların homeomorf olduğunu kanıtlamak için karşılık gelen dönüşümü belirtmek yeterlidir, ancak bazı şekiller için bir dönüşüm bulamamamız bu rakamların homeomorfik olmadığını kanıtlamaz. Topolojik özellikler burada yardımcı olur.
topolojik özellik(veya topolojik değişmez) geometrik şekillerin, belirli bir şekille birlikte, topolojik bir dönüşüm sırasında dönüştüğü herhangi bir şekle de sahip olan bir özelliktir.
En az bir nokta içeren herhangi bir açık bağlantılı kümeye denir. alan.
Herhangi bir kapalı basit (yani, bir daireye homeomorfik) eğrinin bir noktaya kadar daraltılabildiği ve her zaman bu bölgede kalan bir bölgeye denir. basitçe bağlı basit bağlantı... Bu alanın kapalı bir basit eğrisi bir noktaya kadar çekilemiyor ve sürekli bu alanda kalıyorsa o alana alan denir. çoklu bağlantılı, ve bölgenin karşılık gelen özelliği çoklu bağlantı... Biri deliksiz ve diğeri delikli iki dairesel bölge veya disk hayal edin. İlk bölge basitçe bağlantılıdır, ikincisi çoklu bağlantılıdır. Tekli bağlantı ve çoklu bağlantı topolojik özelliklerdir. Deliği olan bir bölge, homeomorfizma altında deliksiz bir bölgeye dönüştürülemez. İlginçtir ki, çoklu bağlantılı bir diskte, her bir delikten diskin kenarına kadar kesim boyunca çizersek, o zaman basitçe bağlantılı hale gelir.
Kapalı bir yüzeyin ayrı parçalara ayrılmadan kesilebileceği maksimum kapalı basit ayrık eğri sayısına denir. doğuştan yüzey. Cins, bir yüzeyin topolojik değişmezidir. Kürenin cinsinin sıfır olduğu, torus cinsinin ("çörek" yüzeyinin) bir olduğu, simit cinsinin (iki delikli torus) iki olduğu, yüzeyin cinsinin iki olduğu kanıtlanabilir. P delikler P... Buradan ne küpün yüzeyinin ne de kürenin simit için homeomorfik olmadığı sonucu çıkar.
Yüzeyin topolojik değişmezleri arasında kenar sayısı ve kenar sayısı da not edilebilir. Diskin 2 kenarı, 1 kenarı ve 0 cinsi vardır. Torusun 2 kenarı vardır, kenarları yoktur ve cinsi 1'dir.
Yukarıda tanıtılan kavramlar, topolojinin tanımını netleştirmeyi mümkün kılmaktadır: topoloji, homeomorfizmalar altında korunan özellikleri inceleyen bir matematik dalıdır..
Önemli sorunlar ve sonuçları.
Ürdün kapalı eğri teoremi.
Yüzeye basit bir kapalı eğri çizilirse, yüzey deforme olduğunda eğrinin korunan herhangi bir özelliği var mıdır? Böyle bir özelliğin varlığı aşağıdaki teoremden çıkar: bir düzlem üzerindeki basit bir kapalı eğri, düzlemi iç ve dış olmak üzere iki bölgeye ayırır.... Bu görünüşte önemsiz teorem, örneğin bir daire için basit bir formun eğrileri için açıktır; ancak karmaşık kapalı çokgen çizgiler için durum farklıdır. Teorem ilk olarak C. Jordan (1838–1922) tarafından formüle edilmiş ve kanıtlanmıştır; ancak Jordan'ın kanıtının yanlış olduğu ortaya çıktı. 1905'te O. Weblen (1880-1960) tarafından tatmin edici bir kanıt önerildi.
Brouwer sabit nokta teoremi.
İzin vermek NS- bir daire ve iç kısmından oluşan kapalı bir alan. Brouwer teoremi, etki alanının her noktasını alan herhangi bir sürekli dönüşüm için şunu belirtir: NS aynı alanda bir noktaya kadar, bu dönüşüm sırasında sabit kalan bir nokta vardır. (Dönüşümün birebir olması gerekmez.) Brouwer'ın sabit nokta teoremi özellikle ilgi çekicidir çünkü matematiğin diğer dallarında en sık kullanılan topolojik teorem gibi görünmektedir.
Dört renk sorunu.
Sorun şudur: Herhangi bir harita, ortak bir sınırı olan herhangi iki ülkenin farklı renklerde boyanması için dört renkle renklendirilebilir mi? Dört renk sorunu topolojiktir, çünkü ne ülkelerin şekli ne de sınırların konfigürasyonu önemli değildir.
Herhangi bir haritanın renklendirilmesi için dört rengin yeterli olduğu hipotezi ilk olarak 1852'de ifade edildi. Deneyimler, dört rengin gerçekten yeterli olduğunu göstermiştir, ancak yüz yılı aşkın bir süredir kesin bir matematiksel kanıt elde edilememiştir. Ve sadece 1976'da Illinois Üniversitesi'nden K. Appel ve W. Haken, 1000 saatten fazla bilgisayar zamanı harcayarak başarıya ulaştı.
Tek taraflı yüzeyler.
En basit tek taraflı yüzey Mobius yaprağı, 1858'de olağanüstü topolojik özelliklerini keşfeden A. Möbius'un onuruna böyle adlandırılmıştır. ABCD(incir. 2, a) Dikdörtgen bir kağıt şerididir. noktayı yapıştırırsanız A nokta ile B ve nokta C nokta ile NS(incir. 2, B), iç yüzeyi, dış yüzeyi ve iki kenarı olan bir halka elde edersiniz. Halkanın bir tarafı (şek. 2, B) renklendirilebilir. Boyalı yüzey, halkanın kenarlarıyla sınırlanacaktır. Böcek, boyalı veya boyasız bir yüzeyde kalarak halkanın etrafında "dünyayı dolaşabilir". Ancak, uçları yapıştırmadan önce şeridi yarım tur bükerseniz ve noktayı yapıştırırsanız A nokta ile C, a B ile birlikte NS, sonra bir Mobius şeridi elde edersiniz (Şekil 2, v). Bu şeklin sadece bir yüzeyi ve bir kenarı vardır. Mobius şeridinin yalnızca bir tarafını boyamaya yönelik herhangi bir girişim, Mobius şeridinin yalnızca bir tarafı olduğundan başarısızlığa mahkumdur. Mobius yaprağının ortasında sürünen bir böcek (kenarları geçmeden) baş aşağı pozisyonda başlangıç noktasına dönecektir. Bir Mobius yaprağını orta hat boyunca keserken iki parçaya bölünmez.
Düğümler.
Bir düğüm, uzayda birbirine bağlı uçları olan karışık bir ince ip parçası olarak düşünülebilir. En basit örnek, bir ip parçasından ilmek yapmak, uçlarından birini ilmek içinden geçirmek ve uçlarını bağlamaktır. Sonuç olarak, nasıl gerilir veya bükülürse bükülsün, tek tek noktaları kırmadan veya yapıştırmadan topolojik olarak aynı kalan kapalı bir eğri elde ederiz. Topolojik değişmezler sistemine göre düğümleri sınıflandırma sorunu henüz çözülmemiştir.





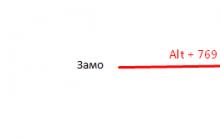




Taramalı Atomik Kuvvet Mikroskobu Laboratuvar raporu şunları içermelidir:
Havai iletişim ağı desteklerinin raflarının seçimi
AC katener tasarımı ve hesaplanması
Mikroişlemci sistemlerinin geliştirilmesi Mikroişlemci sistemlerinin tasarım aşamaları
mcs51 ailesinin mikrodenetleyicileri