Odošlite svoju dobrú prácu do znalostnej bázy je jednoduché. Použite nasledujúci formulár
Študenti, doktorandi, mladí vedci, ktorí využívajú vedomostnú základňu pri štúdiu a práci, vám budú veľmi vďační.
Zverejnené dňa http://www.allbest.ru/
1. Pri riešení výrobných a ekonomických problémov sa používajú metódy lineárneho programovania
Techniky lineárneho programovania sú určené na optimalizačné problémy týkajúce sa funkcií lineárnej zdatnosti alebo prietoku s lineárnymi obmedzeniami na parametre alebo vstupné premenné. Na riešenie problémov s alokáciou aktív sa bežne používa lineárne programovanie. Vo svete obchodovania je jednou z možných aplikácií lineárneho programovania hľadanie optimálneho rozdelenia finančných prostriedkov do rôznych finančných nástrojov pre maximálny zisk. Ak je zisk optimalizovaný s ohľadom na možné riziko, potom nemožno použiť lineárne metódy. Výnos upravený o riziko nie je lineárnou funkciou váh rôznych investícií do celkového portfólia; sú tu potrebné ďalšie metódy, napríklad genetické algoritmy.
2. Grafická metóda založenáo geometrickej interpretácii predávať lineárne programovanie
1. Graficky je možné vyriešiť:
Úlohy uvedené v štandardnom formulári, ktorý obsahuje najviac dve premenné;
Problémy uvedené v kanonickej forme s počtom voľných premenných (r je poradie matice systému obmedzení);
Všeobecné problémy, ktoré po redukcii na kanonickú formu budú obsahovať najviac dve voľné premenné.
2. Hlavnou formou grafického riešenia je prvý typ problému. Preto ak sa vyskytne druhý alebo tretí typ problému, potom sa ich model musí najskôr zredukovať na prvý typ.
3. Technika riešenia úloh LP grafickou metódou
I. V obmedzeniach problému nahraďte znaky nerovností znakmi presnej rovnosti a zostrojte zodpovedajúce úsečky.
II. Nájdite a vytieňujte poloroviny, ktoré sú vyriešené každou z nerovností obmedzenia problému. Ak to chcete urobiť, musíte nahradiť súradnice bodu [napríklad (0; 0)] konkrétnou nerovnosťou a skontrolovať pravdivosť výslednej nerovnosti. Ak je nerovnosť pravdivá, je potrebné zatieniť polorovinu obsahujúcu daný bod; inak (nerovnosť je nepravdivá), je potrebné zatieniť polrovinu, ktorá daný bod neobsahuje.
Pretože a musia byť nezáporné, ich prípustné hodnoty budú vždy nad osou a napravo od osi, t.j. v kvadrante I.
Obmedzenia rovnosti umožňujú iba tie body, ktoré ležia na zodpovedajúcej čiare. Preto je potrebné takéto rovné čiary v grafe zvýrazniť.
III. Definujte ODR ako časť roviny, ktorá patrí do všetkých povolených oblastí súčasne, a vyberte ju. Ak chýba IDT, problém nemá riešenie.
IV. Ak ODR nie je prázdna množina, musíte vytvoriť cieľový riadok, t.j. ktorákoľvek z úrovňových čiar (kde L je ľubovoľné číslo, napríklad násobok a, teda vhodné pre výpočty). Metóda výstavby je podobná konštrukcii priamych obmedzení.
V. Zostrojte vektor, ktorý začína v bode (0; 0) a končí v bode. Ak sú cieľová čiara a vektor zostavené správne, budú kolmé.
VI. Pri hľadaní maxima CF je potrebné posúvať cieľovú čiaru v smere vektora, pri hľadaní minima CF je potrebné pohybovať sa proti smeru vektora. Posledným vrcholom ODR pozdĺž pohybu bude maximálny alebo minimálny bod CF. Ak taký bod (body) neexistuje, môžeme dospieť k záveru, že CF je bez obmedzenia na množine plánov zhora (pri hľadaní maxima) alebo zdola (pri hľadaní minima).
VII. Určte súradnice bodu max (min) DF a vypočítajte hodnotu DF. Na výpočet súradníc optimálneho bodu je potrebné vyriešiť sústavu rovníc priamok, ktorých priesečník je.
4 ... Ako zostaviť počiatočný plán problému LP jednoduchou metódou a skontrolovať jeho optimálnosť
Pre nájdenie referenčného riešenia je potrebné uviesť základné premenné (premenné, ktoré boli v systéme obmedzení pred prenesením do kanonickej podoby, nazývajú sa hlavné premenné úlohy), na nulu, potom sa ďalšie premenné budú rovnať zodpovedajúcim voľným členom. Plán sa považuje za optimálny pri riešení maximálneho problému, ak v indexovom riadku nie sú záporné koeficienty. Pri riešení minimálneho problému sú naopak koeficienty radu C nezáporné.
5 ... Ako definovať premennú (vektor), ktorá sa má zahrnúť do základu, a premennú (vektor), ktorá sa má vylúčiť zo základne
Na určenie, ktorá z premenných musí byť zadaná do základu, je potrebné nájsť rozlišovací stĺpec. Aby sme to dosiahli, pozrieme sa na riadok indexu simplexovej tabuľky: obsahujúci najväčší záporný prvok v absolútnej hodnote, ak problém vyriešime na minime, potom najväčší kladný. Na určenie premennej, ktorú je potrebné odvodiť zo základu, je definovaný reťazec riešenia. Na jeho určenie je potrebné vypočítať, či úlohu vyriešime na maximum, potom bude stĺpec riešenia simplexný vzťah.
Simplexná relácia (Q) \u003d Členovia stĺpca voľného člena
Zodpovedajúce prvky stĺpca povolení
Hodnoty simplexného pomeru sú uvedené v tabuľkách.
Spomedzi získaných pomerov je zvolený najmenší nezáporný simplexný pomer, a to ako pri riešení úlohy na minimum, tak aj pri riešení na maximum. Nula simplexného vzťahu definuje rozlišovací reťazec, ak menovateľ tohto pomeru obsahuje kladné číslo. Ak je získaných niekoľko rovnakých simplexných vzťahov, potom je ako riešiaci vybraný ktorýkoľvek riadok. Na priesečníku riešiaceho riadku a stĺpca je riešiaci prvok.
6 ... Aká metóda riešenia sústav lineárnych rovníc je základom simplexovej metódy
Určenie východiskového podporného riešenia a prechod na ďalšie podporné riešenie sa uskutočňuje na základe aplikácie Jordan-Gaussovej metódy pre systém lineárnych rovníc kanonického tvaru, v ktorom musí byť vopred napísaný počiatočný LPP; smer prechodu z jedného referenčného riešenia na druhé sa volí na základe kritéria optimality (objektívnej funkcie) pôvodného problému.
7. Popíšte algoritmus simplexovej metódy
Schéma riešenia problému lineárneho programovania pomocou simplexnej metódy pozostáva z nasledujúcich hlavných etáp. 1. Matematická formalizácia problému; 2. uvedenie systému obmedzení do kanonickej podoby; 3. Hľadanie referenčného riešenia a hľadanie základu problému; 4. Zostavenie prvého simplexného stola; 5. Kontrola optimality plánu; 6. Neustále zlepšovanie plánu na získanie optimálneho plánu.
8. Popíšte pravidlá konštrukcie problému duálneho LP
Pravidlá pre konštrukciu dvojakých problémov:
Záznam pôvodného problému je usporiadaný (ak je objektívna funkcia maximalizovaná, potom by obmedzenia nerovnosti mali mať tvar<= если минимизируется то >\u003d), splnenie týchto podmienok sa dosiahne vynásobením zodpovedajúcich obmedzení číslom -1. Ak sa priamy problém vyrieši na maximum, potom je minimálne na duálnej úrovni a naopak. Pre každé obmedzenie priameho problému zodpovedá premenná duálneho problému a naopak. Matica systému obmedzení duálneho problému sa získa z matice systému obmedzení priameho problému transpozíciou. Voľnými pojmami systému obmedzení priameho problému sú koeficienty pre zodpovedajúce premenné objektívnej funkcie duálneho problému a naopak. ale nie, nie je to ako obmedzenie rovnosti. Ak je akékoľvek obmedzenie priameho problému zapísané ako rovnosť, potom podmienka nezápornosti nie je uvalená na zodpovedajúcu premennú duálneho problému.
9 ... Aká je ekonomická interpretácia duálnych hodnotení
Z ekonomického hľadiska možno dvojakú úlohu interpretovať takto:
aká by mala byť jednotková cena každého zo zdrojov, aby sa minimalizovali celkové náklady na náklady pre dané množstvo zdrojov b i a hodnoty jednotkových nákladov C j? A počiatočný problém definujeme takto: koľko a akých produktov xj (j \u003d 1,2, ..., n) je potrebné vyrobiť tak, aby za dané náklady C j (j \u003d 1,2, ..., n) bola produkčná jednotka a veľkosť dostupných zdrojov bi (i \u003d 1,2, ..., n) na maximalizáciu výroby v hodnotovom vyjadrení.
1 0 ... Ako sa určujú duálne odhady z poslednej simplexnej tabuľky
Pri hľadaní riešenia duálneho problému najskôr nájdeme riešenie pôvodného problému metódou na umelom základe. Posledná simplexná tabuľka ukazuje, že duálny problém má riešenie.
1 1 ... Sformulujte problém optimálneho plánovania výroby a zapíšte si ho ako model LP
Niektoré podniky vyrábajú n druhov výrobkov a utrácajú m druhov zdrojov. Známe sú tieto parametre: aij - množstvo i-tého zdroja potrebného na výrobu jednotkového množstva j-tého produktu; aij0 (i \u003d 1, ..., m; j \u003d 1, ..., n);
b-sklad i-tého zdroja v podniku, bi\u003e 0;
cj je cena jednotkového množstva j-tého produktu, cj\u003e 0.
Predpokladá sa, že náklady na zdroje rastú priamo úmerne s objemom výroby. Nech xj je plánovaný objem výroby j-tého produktu. Potom je prípustná iba taká sada produktov x \u003d (x1, x2, ..., xn), u ktorej celkové náklady na každý typ i-tého zdroja nepresahujú jeho zásoby:
Ďalej máme nasledujúce obmedzenie: xj0; j \u003d 1, ..., n. (2)
Cena súboru výrobkov x sa vyjadruje ako: (3)
Problém plánovania výroby je kladený nasledovne: spomedzi všetkých vektorov x vyhovujúcich obmedzeniam (1), (2) nájdite taký, pre ktorý má hodnota (3) najväčšiu hodnotu.
1 2 ... Sformulujte problém optimálneho zloženia zmesi a zapíšte si ho ako model LP
Nech existuje m druhov surovín, ktorých zásoby sú d1, ..., dm. Z tejto suroviny je potrebné vyrobiť zmes obsahujúcu n látok, ktoré určujú technické vlastnosti zmesi. Známe sú množstvá aij (i \u003d 1, m; j \u003d 1, n), ktoré určujú množstvo j-tej látky v jednotke i-tého druhu suroviny, ktorej cena sa rovná ci (i \u003d 1, m), ako aj bj (j \u003d 1 , n) je najmenšie prípustné množstvo j-tej látky v zmesi.
Je potrebné získať zmes s požadovanými vlastnosťami pri čo najnižších nákladoch na suroviny.
Cieľom úlohy (objektívna funkcia) je minimalizovať celkové náklady na suroviny.
Nájdite vektor X \u003d (x 1, x 2, ..., x n) vyhovujúci systému obmedzení:
a dodanie minimálnej hodnoty objektívnej funkcii.
1 3 ... Sformulujte problém transportu LP a zapíšte si jeho model
Problém s dopravou je jedným z najbežnejších problémov v matematickom programovaní (zvyčajne lineárny). Vo všeobecnosti to možno znázorniť nasledovne: je potrebné nájsť taký plán dodávky tovaru od dodávateľov k spotrebiteľom, aby náklady na prepravu (alebo celková vzdialenosť alebo objem prepravných prác v tonokilometroch) boli čo najmenšie. V dôsledku toho sa scvrkáva na najracionálnejšie pripútanie výrobcov k spotrebiteľom a naopak. V najjednoduchšej podobe, keď sa distribuuje jeden typ produktu a spotrebiteľom je jedno, od ktorého dodávateľa ho majú dostať, je problém formulovaný takto.
Základné informácie:
Mi je počet nákladných jednotiek v i-tom bode odchodu (i \u003d 1, 2, ..., k);
Nj - potreba j-tého cieľa (j \u003d 1, 2, ..., l) (v nákladných jednotkách);
aij - náklady na prepravu jednotky nákladu z i-tého bodu do j-tého bodu.
Označme xij plánovaný počet nákladných jednotiek na prepravu z bodu i-ro do j-tého.
V prijatej notácii:
Celkové (celkové) náklady na prepravu;
Množstvo vyvážaného nákladu z bodu i-ro;
Množstvo nákladu dodaného do bodu j.
V najjednoduchšom prípade musia byť splnené tieto zrejmé podmienky:
Matematická formulácia problému v doprave bude teda:
za podmienok:
Tento problém sa nazýva uzavretý (uzavretý, vyvážený) model dopravy. Podmienkou je prirodzená podmienka riešiteľnosti uzavretého dopravného problému. Všeobecnejším dopravným problémom je takzvaný otvorený (nevyvážený) dopravný model:
za podmienok:
1 4 . Ktoré dopravné problémové modely sa nazývajú otvorené a ako previesť otvorený model na uzavretý?
Pre vyriešiteľnosť problému s dopravou je nevyhnutné a dostatočné, aby sa zásoby v miestach odchodu rovnali potrebám nákladu v cieľových bodoch. Ak je splnená podmienka vyváženia, potom sa model problému s prenosom nazýva uzavretý. Ak nie je splnená podmienka vyváženia, potom sa model problému s prenosom nazýva otvorený. Na získanie uzavretého modelu sa zavádza ďalšia (fiktívna) základňa so zásobou chýbajúceho nákladu.
Ak je do modelu zavedený fiktívny (m + 1) -tý dodávateľ, pre ktorý sa skladová zásoba rovná rozdielu medzi celkovým dopytom spotrebiteľov a skutočnou skladovou zásobou dodávateľov. Všetky tarify za dodanie tovaru od fiktívneho dodávateľa sa považujú za rovné 0 :. Jeden riadok sa pridá do transportnej tabuľky.
Do modelu je zavedený fiktívny (n + 1) spotrebiteľ, po ktorom sa dopyt rovná rozdielu medzi celkovou ponukou dodávateľov. Všetky tarify za dodanie tovaru s fiktívnymi potrebami sa považujú za rovné 0 :. Jeden stĺpec sa pridá do transportnej tabuľky.
15 ... Potenciálna metóda
Metóda potenciálov je rozšírená metóda na riešenie dopravných problémov. Ak je uskutočniteľné riešenie (i \u003d 1,2, ..., m; j \u003d 1,2, ... n) dopravného problému optimálne, potom existujú potenciály (počty) dodávateľov (i \u003d 1,2, ..., m) a spotrebiteľov (j \u003d 1,2, ..., n). Podporné riešenie je optimálne, ak odhady nie sú pozitívne pre všetky vektory stavu (bunky tabuľky). Algoritmus riešenia dopravných problémov potenciálnou metódou:
a) skontrolovať splnenie nevyhnutných a dostatočných podmienok na riešenie problému. Ak má úloha nesprávnu rovnováhu, potom sa predstaví fiktívny dodávateľ alebo spotrebiteľ s chýbajúcimi zásobami alebo požiadavkami a nulovými nákladmi na prepravu. b) zostavte riešenie počiatočnej podpory (metódou minimálnych nákladov alebo inou metódou), skontrolujte správnosť jej konštrukcie počtom obsadených buniek (malo by ich byť m + n-1) a uistite sa, že vektory podmienok sú lineárne nezávislé (použije sa metóda delécie). c) vybudovať systém potenciálov zodpovedajúci referenčnému riešeniu. Za týmto účelom je vyriešený systém rovníc, ktorý má nekonečné množstvo riešení. Na nájdenie konkrétneho riešenia systému je jednému z potenciálov (obvykle takému, ktorý zodpovedá väčšiemu počtu obsadených buniek) ľubovoľne priradená nejaká hodnota (zvyčajne nula). Zvyšok potenciálov je jednoznačne určený vzorcami. d) skontrolujte splnenie podmienky optimality pre voľné bunky tabuľky. Za týmto účelom sa odhady pre všetky voľné bunky vypočítajú pomocou vzorcov a tie z nich, ktoré sú väčšie ako nula, sa zapíšu do ľavého dolného rohu buniek. Ak pre všetky voľné bunky, potom sa vypočíta hodnota objektívnej funkcie a riešenie problému sa skončí, pretože získané riešenie je optimálne. Ak existuje aspoň jedna bunka s pozitívnym skóre, riešenie podpory nie je optimálne.
e) prejsť na referenčné riešenie, pri ktorom bude hodnota objektívnej funkcie menšia. Ak to chcete urobiť, vyhľadajte bunku tabuľky úloh, ktorá zodpovedá najvyššiemu kladnému skóre. Je zostavený cyklus, ktorý obsahuje túto bunku a časť buniek obsadených podporným riešením. V bunkách cyklu striedajte znamienka „+“ a „-“, začínajúce od „+“ v bunke s najvyšším pozitívnym skóre. Posun (prerozdelenie zaťaženia) sa vykonáva v priebehu cyklu o určitú hodnotu. Bunka so znamienkom „-“, v ktorej je dosiahnutá, zostáva prázdna. Ak je minimum dosiahnuté vo viacerých bunkách, potom jedna z nich zostáva prázdna a vo zvyšku sú nastavené základné nuly, takže počet obsadených buniek zostáva rovnaký. Potom prejdite na krok 3 tohto algoritmu.
MODELY PLÁNOVANIA SIETE
1. Aké sú ciele uplatňovania metód SPM? Popíšte oblasť použitia sieťových metód v systéme Windowsekonomika
Sieťové plánovanie je komplex grafických a výpočtových metód organizačných opatrení, ktoré poskytujú modelovanie, analýzu a dynamickú reštrukturalizáciu plánu na implementáciu zložitých projektov a vývojov, napríklad: výstavba a rekonštrukcia akýchkoľvek objektov; vykonávanie výskumných a vývojových prác; príprava výroby na výrobu; prezbrojenie armády. Charakteristickou črtou takýchto projektov je, že pozostávajú z množstva samostatných, základných diel. Vzájomne sa podmieňujú tak, že niektoré práce nemôžu byť zahájené skôr, ako sú niektoré dokončené. Hlavným cieľom plánovania a riadenia siete je skrátenie trvania projektu na minimum. Úlohou plánovania a riadenia siete je graficky, vizuálne a systematicky zobrazovať a optimalizovať postupnosť a vzájomnú závislosť prác, činností alebo činností, ktoré zabezpečujú včasné a systematické dosiahnutie konečných cieľov.
Systém SPU umožňuje:
Zostaviť harmonogram vykonávania určitého súboru prác; identifikovať a mobilizovať rezervy času, práce, materiálnych a finančných zdrojov; - riadiť komplex prác na princípe „vedúceho spojenia“ s predpovedaním a predchádzaním možným prerušeniam pri práci; - zlepšiť efektívnosť riadenia ako celku s jasným rozdelením zodpovednosti medzi manažérmi na rôznych úrovniach a osobami vykonávajúcimi prácu; - jasne zobraziť rozsah a štruktúru riešeného problému, identifikovať sa s požadovaným stupňom podrobnosti práce, ktorá tvorí jeden komplex procesu riešenia problému; - - určovať udalosti, ktorých spáchanie je nevyhnutné na dosiahnutie stanovených cieľov; - identifikovať a komplexne analyzovať vzťah medzi dielami, pretože samotná technika budovania sieťového modelu obsahuje presný odraz všetkých závislostí od stavu objektu a podmienok vonkajšieho a vnútorného prostredia; - vo veľkej miere využívať výpočtovú techniku; - rýchlo spracovať veľké množstvo údajov z výkazov a poskytnúť vedeniu včasné a komplexné informácie o skutočnom stave vykonávania programu; - - zjednodušiť a zjednotiť spravodajskú dokumentáciu.
2. Čo je sieťový graf?
Sieťový model je plán implementácie určitého súboru vzájomne prepojených diel špecifikovaných vo forme siete, ktorého grafické znázornenie sa nazýva sieťový diagram.
3. Čo sa myslí pod pojmami práca a udalosti, akotypy práce, ktoré poznáš?
Sieťové modely sa skladajú z nasledujúcich troch prvkov:
Práca (alebo úloha) Udalosť (míľniky) Komunikácia (závislosť)
Práca (aktivita) - proces, ktorý je potrebné vykonať, aby ste dosiahli určitý (daný) výsledok, zvyčajne vám umožňujú začať ďalšie aktivity. Pojmy „úloha“ a „práca“ môžu byť totožné, ale v niektorých prípadoch sa úlohy zvyčajne nazývajú vykonávanie akcií, ktoré idú nad rámec priamej výroby, napríklad „Kontrola projektovej dokumentácie“ alebo „Rokovania so zákazníkom“. Niekedy sa pojem „úloha“ používa na vyjadrenie činností na najnižšej úrovni v hierarchii. Udalosť (uzol) - okamih, keď sa zmení stav systému, najmä okamih začiatku alebo konca akejkoľvek práce je vo svojej podstate udalosťou a každé dielo musí mať nevyhnutne počiatočnú a záverečnú udalosť. Práca je akcia alebo proces, ktoré musia nastať, aby sa mohol presunúť z počiatočnej udalosti do konečnej udalosti. Niektoré udalosti sú spoločné pre niekoľko úloh, v tomto prípade je výskytom okamih zodpovedajúci dokončeniu poslednej z úloh bezprostredne predchádzajúcich tejto udalosti. Medzník je typ udalosti, ktorá charakterizuje dosiahnutie významných priebežných výsledkov (samostatné etapy projektu). Prepojenie je logický vzťah medzi načasovaním individuálnej práce a výskytom udalostí. Ak je na to, aby bolo možné začať vykonávať akúkoľvek prácu, potrebné dokončiť ďalšiu prácu, hovoria, že tieto práce sú spojené odkazom (spojené). Vzťahy v ich podstate môžu byť určené technológiou práce alebo ich organizáciou. Podľa toho sa rozlišujú technologické a organizačné typy väzieb. Vzťahy sa dajú tiež nazvať závislosťami (Relationship) alebo figurínami (Dummy Activity). Spojenia nevyžadujú výkonných umelcov a priame investovanie času, ale je možné ich charakterizovať predĺžením trvania (kladné, záporné alebo nulové).
4. Popíšte hlavné požiadavky, ktoré majú byťmôže uspokojiť sieťový plán
Pri vytváraní sieťového diagramu musíte dodržiavať niekoľko pravidiel.
1. V sieťovom modeli by nemali existovať žiadne „slepé“ udalosti, to znamená udalosti, z ktorých neodchádza žiadna práca, s výnimkou ukončovacej udalosti. Tu buď práca nie je potrebná a musí byť zrušená, alebo nie je zaznamenaná potreba určitej práce nasledujúcej po udalosti na splnenie nejakej nasledujúcej udalosti. V takýchto prípadoch je potrebné starostlivo študovať vzťah udalostí a pracovať na náprave vzniknutého nedorozumenia.
2. V pláne siete by nemali byť žiadne „chvostové“ udalosti (okrem počiatočnej), ktorým by predchádzala najmenej jedna úloha. Po nájdení takýchto udalostí v sieti je potrebné určiť umelcov predchádzajúcich diel a zahrnúť ich do siete.
3. Sieť by nemala mať uzavreté slučky a slučky, to znamená cesty spájajúce niektoré udalosti so sebou. Keď sa objaví kontúra (a v zložitých sieťach, to znamená v sieťach s vysokým indexom zložitosti, stáva sa to pomerne často a je zistená iba pomocou počítača), je potrebné sa vrátiť k pôvodným údajom a revíziou rozsahu práce dosiahnuť ich elimináciu.
4. Akékoľvek dve udalosti musia byť priamo spojené najviac štyrmi šípkami. Porušenie tejto podmienky nastáva pri zobrazovaní súbežnej práce. Ak tieto diela ponecháte tak, ako sú, dôjde k zámene z dôvodu, že dve rôzne diela budú mať rovnaké označenie. Obsah týchto prác, zloženie zúčastnených dodávateľov a množstvo zdrojov vynaložených na práce sa však môžu výrazne líšiť.
5. Ako sa určujú časové odhady pracovných miest a udalostí?
Začiatok a koniec akejkoľvek práce je opísaný dvojicou udalostí, ktoré sa nazývajú udalosti začiatku a konca. Preto sa na označenie konkrétneho diela používa pracovný kód P i, j, ktorý sa skladá z čísel počiatočných (i-tých) a konečných (j-tých) udalostí (obr. 1, a). Obrázok 1, b zobrazuje príklad kódovania práce a udalostí v prijatej notácii: t ij - trvanie práce Р i, j, t - skorý dátum (očakávaný okamih) udalosti, t * - neskorý dátum (maximálny okamih) udalosti, n - číslo udalosti, n cm - číslo predchádzajúcej (susednej) udalosti.
Obr. Označenie prvkov sieťového diagramu: a - pracovný kód; b - príklad kódovacích udalostí v prijatých označeniach; c - príklad obrazu udalosti vo vyššie uvedenom zápise.
Obrázok 1c zobrazuje príklad obrazu udalosti vo vyššie uvedenom zápise. Označme to súborom úloh zahrnutých do j-tej udalosti a - súborom úloh vznikajúcich z i-tej udalosti. Skorý dátum (očakávaný okamih) j-tej udalosti je časový okamih, pred ktorým k udalosti nemôže dôjsť, a je vypočítaný podľa vzorca
Neskorý čas (limitujúci moment) i-tej udalosti ukazuje maximálne oneskorenie v čase výskytu tejto udalosti:
6. Rozšírte obsah, metódu definície a význam kritickej cestyv modeloch plánovania siete
Kritická cesta je sled činností medzi počiatočnými a konečnými udalosťami v sieti, ktoré majú najväčšie časové trvanie. Minimálny čas potrebný na dokončenie projektu zapojeného do siete sa rovná dĺžke kritickej cesty. Sieťový diagram môže obsahovať nie jednu, ale niekoľko kritických ciest. Práce a udalosti nachádzajúce sa na tejto ceste sa tiež nazývajú kritické. Interval rezervy od t do t * pre udalosti ležiace na kritickej ceste je 0. Pre konečnú sieťovú udalosť musí byť neskorý dátum udalosti rovný jej skorému dátumu, to znamená t p \u003d t * p. Dĺžka kritickej cesty je rovná skorému dátumu dokončenie udalosti, t. j. t cr \u003d t p \u003d t * p.
PROBLÉMY TEÓRIE HROMADNEJ SLUŽBY
1. Aké systémy sa vyšetrujú pomocou teórie čakania v rade?
Z hľadiska modelovania procesu čakania na rad nastávajú situácie, keď sa tvoria rady požiadaviek (požiadaviek) na obsluhu. Po vstupe do obslužného systému sa žiadosť pripojí do frontu ďalších (predtým prijatých) požiadaviek. Servisný kanál vyberie požiadavku od tých, ktorí sú vo fronte, aby ju mohol začať obsluhovať. Po dokončení servisného postupu pre ďalšiu požiadavku začne obslužný kanál obsluhovať ďalšiu požiadavku, ak je v čakajúcom bloku. Cyklus fungovania tohto systému radenia sa opakuje mnohokrát počas celej doby prevádzky obsluhujúceho systému. V takom prípade sa predpokladá, že prechod systému na obsluhu nasledujúceho zákazníka po dokončení servisu predchádzajúceho zákazníka nastáva okamžite, v náhodných časoch.
2. Pozrite si príklady systémov čakania v radeiya v ekonomike, vo výrobe
Príklady systémov čakania v rade sú: · miesta na údržbu automobilov; · Osobné počítače slúžiace na prichádzajúce aplikácie alebo požiadavky na riešenie určitých problémov; · Útvary daňových inšpektorátov zaoberajúce sa prijímaním a overovaním aktuálneho výkazníctva podnikov; · Audítorské spoločnosti; · Telefónne ústredne atď.
3. Ako sú klasifikované systémy čakania na rad?
SOT sú rozdelené do rôznych skupín v závislosti od zloženia a času stráveného vo fronte pred začiatkom služby a od disciplíny vybavovania požiadaviek. Podľa zloženia SOT existujú jednokanálové (s jedným servisným zariadením) a viackanálový (s veľkým počtom servisných zariadení). Viackanálové systémy môžu pozostávať z obslužných zariadení rovnakého alebo rozdielneho výkonu.
Podľa času, ktorý zostáva vo fronte pred začiatkom údržby, sú systémy rozdelené do troch skupín:
1) s neobmedzenou dobou čakania (s čakaním),
2) s odmietnutiami;
3) zmiešaný typ.
4. Aké sú vlastnosti najjednoduchšieho streamu?
Najjednoduchší stream má nasledujúce dôležité vlastnosti:
1) Vlastnosť stacionarity, ktorá vyjadruje nemennosť pravdepodobnostného režimu toku v čase. To znamená, že počet požiadaviek vstupujúcich do systému v pravidelných intervaloch by mal byť v priemere konštantný. Napríklad počet vagónov prichádzajúcich na naloženie v priemere za deň by mal byť rovnaký pre rôzne časové obdobia, napríklad na začiatku a na konci desaťročia.
2) Absencia aftereffectu, ktorý určuje vzájomnú nezávislosť príchodu určitého počtu servisných požiadaviek v neprekrývajúcich sa časových intervaloch. To znamená, že počet požiadaviek prichádzajúcich v danom časovom intervale nezávisí od počtu vybavených požiadaviek v predchádzajúcom časovom intervale. Napríklad počet vozidiel, ktoré dorazili na materiál desiaty deň v mesiaci, nezávisí od počtu vozidiel obsluhovaných štvrtý alebo ktorýkoľvek predchádzajúci deň v mesiaci.
3) Vlastnosť ordinárnosti, ktorá vyjadruje praktickú nemožnosť súčasného príchodu dvoch alebo viacerých požiadaviek (pravdepodobnosť takejto udalosti je v porovnaní s uvažovaným časovým obdobím, keď je druhá smerovaná na nulu, nemerateľne malá).
Pri najjednoduchšom toku pohľadávok sa distribúcia pohľadávok vstupujúcich do systému riadi Poissonovým distribučným zákonom:
pravdepodobnosť, že obsluhujúci systém prijme presne k zákazníkov v čase t:
kde. - priemerný počet prijatých žiadostí o službu za jednotku času.
5. Aké rozdelenie má zvyčajne čas služby?
Jednou z najdôležitejších charakteristík servisných zariadení, ktorá určuje priepustnosť celého systému, je čas služby. Doba služby jednej požiadavky () je náhodná premenná, ktorá sa môže meniť v širokom rozmedzí. Závisí to od stability činnosti samotných obslužných zariadení, ako aj od rôznych parametrov vstupujúcich do systému, požiadaviek (napríklad rôzna nosnosť vozidiel prichádzajúcich na nakládku alebo vykládku). Náhodná premenná je úplne charakterizovaná zákonom o rozdelení, ktorý sa určuje na základe štatistických testov.
V praxi sa najčastejšie prijíma hypotéza o zákone exponenciálneho rozdelenia času služby.
Zákon exponenciálneho rozloženia času služby nastane, keď hustota distribúcie prudko klesá so zvyšujúcim sa časom t. Napríklad keď sa väčšina požiadaviek vybaví rýchlo a dlhodobá služba je zriedkavá. Existencia zákona exponenciálneho rozdelenia času služby je stanovená na základe štatistických pozorovaní.
Pri exponenciálnom zákone distribúcie času služby je pravdepodobnosť udalosti, že čas služby nebude trvať dlhšie ako t, je:
kde v je intenzita obsluhy jedného zákazníka jedným obsluhovacím zariadením, ktorá sa určuje z pomeru:
kde je priemerná doba vybavovania jednej požiadavky jedným servisným zariadením.
Je potrebné poznamenať, že ak je zákon rozloženia času služby exponenciálny, potom za prítomnosti viacerých obslužných zariadení rovnakej sily bude mať zákon o rozložení času služby aj niekoľko indikatívnych prvkov:
kde n je počet servisných zariadení.
6. Aká je praktická aplikácia teórie čakania v rade pri analýze fungovania EÚ?lenivosť výroby?
Aplikácia systému radenia sa používa pri problémoch, keď sú hromadne prijímané žiadosti o službu s ich následnou spokojnosťou. V praxi to môže byť príjem surovín, materiálov, polotovarov, výrobkov do skladu a ich prepustenie zo skladu; spracovanie širokej škály dielov na rovnakom technologickom zariadení; organizácia nastavenia a opráv zariadení; dopravné operácie; plánovanie rezerv a bezpečných zásob zdrojov; stanovenie optimálneho počtu oddelení a služieb podniku; spracovanie plánovacej a reportovacej dokumentácie.
VZORY MEDZIOBOROVEJ BILANCE
1. Oblasť použitia medziodvetvových odvetvízľavy a medziprodukty
Medziodvetvová bilancia (MOB, metóda vstupu a výstupu) je model ekonomickej a matematickej rovnováhy, ktorý charakterizuje medziodvetvové výrobné vzťahy v ekonomike krajiny. Charakterizuje vzťah medzi výstupom v jednom priemysle a nákladmi, výdavkami na výrobky všetkých zúčastnených priemyselných odvetví nevyhnutnými na zabezpečenie tohto výstupu. Zostatok vstupov a výstupov sa zostavuje v hotovosti a v naturáliách.
2. Čo ukazujú a odrážajú súvahové modely?
Medzipriemyselná bilancia je prezentovaná vo forme sústavy lineárnych rovníc. Bilancia vstupov a výstupov (IOB) je tabuľka, ktorá odráža proces formovania a používania agregovaného sociálneho produktu v sektorovom kontexte. V tabuľke je uvedená štruktúra výrobných nákladov na každý výrobok a štruktúra jeho distribúcie v ekonomike. Stĺpce odrážajú hodnotové zloženie hrubej produkcie sektorov hospodárstva podľa prvkov medzispotreby a pridanej hodnoty. Riadky odrážajú využitie zdrojov v jednotlivých priemyselných odvetviach.
3. Daj charakterzačiarknite časti bilančného modelu
V schéme MOB podľa metodiky SNA, rovnako ako v dobre známom otvorenom štatistickom modeli, existujú tri hlavné časti (kvadranty): vnútorný (alebo prvý) kvadrant (I); bočné (alebo pravé) krídlo (II. kvadrant); dolné krídlo (III. kvadrant). IV kvadrant sa nevyvíja. Všeobecná schéma IOB je nasledovná:
Vnútorný (alebo prvý) kvadrant (I) charakterizuje vzájomné prepojenie priemyselných odvetví, odráža medzispotrebu; v II. kvadrante je uvedená štruktúra konečného použitia hrubého domáceho produktu (HDP); III. kvadrant ukazuje štruktúru hrubej pridanej hodnoty podľa prvkov. V kvadrante I („šachová tabuľka“) sa odvetvia hospodárstva zaznamenávajú v riadkoch a stĺpcoch. V stĺpcoch kvadrantu I pre každé odvetvie sú uvedené náklady na výrobu výrobkov, prác, služieb (náklady na suroviny, materiál, palivo, energie, služby) a riadky ukazujú, ako sú výrobky každého odvetvia rozdelené medzi všetky odvetvia. Na pravej strane IOB (// kvadrant) zodpovedajú riadky spotrebnému priemyslu. Stĺpce predstavujú kategórie konečného použitia: konečná spotreba (výdavky na konečnú spotrebu domácností, vlády a neziskové organizácie slúžiace domácnostiam), tvorba hrubého kapitálu (tvorba hrubého fixného kapitálu, zmeny stavu zásob, čisté nadobudnutie hodnôt), exportná bilancia - dovoz tovaru a služieb. Tretí kvadrant predstavuje nákladovú štruktúru HDP. Stĺpce kvadrantu III zodpovedajú spracovateľskému priemyslu a riadky zodpovedajú hlavným nákladovým zložkám hrubej pridanej hodnoty (mzdy zamestnancov, hrubý zisk, hrubý zmiešaný príjem, dane a dotácie súvisiace s výrobou) a daní a dotácií na výrobky. Ak teda uvažujeme údaje MOB vertikálne, potom stĺpce zobrazujú nákladovú štruktúru produkcie jednotlivých priemyselných odvetví, ktorá sa skladá z medzispotreby (kvadrant I) a hrubej pridanej hodnoty (III kvadrant) a horizontálne - po riadkoch - prírodná materiálové zloženie výrobkov, ktoré sa vynakladajú na medzispotrebu (I. kvadrant) a konečné použitie (II. kvadrant). Pre každé odvetvie hospodárstva sa zdroje produktov rovnajú ich použitiu. Štvrtá časť sa nachádza pod druhou. Charakterizuje redistribučné vzťahy v ekonomike uskutočňované prostredníctvom finančného a úverového systému. V plánovaných výpočtoch sa štvrtá časť spravidla nepoužíva, a preto sa nebude brať do úvahy v rámci nášho kurzu.
4 . Popíšte metódy formovania koeficientov priamych nákladov v bilančných modeloch. Ako sa tieto pomery počítajú?
Logické koeficienty, alebo, ako sa tiež nazývajú, koeficienty priamych intraprodukčných nákladov ukazujú, koľko z produktu i-tého odvetvia sa musí minúť na výrobu jednotky hrubého produktu j-tého odvetvia. Koeficienty priamych nákladov sa v statických medzisektorových modeloch považujú za konštantné. Ako možno získať hodnoty aij koeficientov? Existujú dva hlavné spôsoby.
1. Štatistické. Aij koeficienty sa určujú na základe analýzy súvah za predchádzajúce roky. V tomto prípade sa nemennosť koeficientov priamych nákladov v čase dosiahne vhodným výberom sektorov bilancie vstupov a výstupov. Ako ukazuje prax, pri správnom výbere dostatočne veľkých priemyselných odvetví sa aij koeficienty ukážu ako celkom stabilné.
kde Xij a Xj sú prevzaté zo súvahy.
2. Normatívne. Vytvára sa model odvetvia vstupov a výstupov. V tomto modeli sa toto odvetvie považuje za súbor samostatných priemyselných odvetví, pre ktoré už boli vypracované nákladové normy. Ak vopred viete, aké produkty budú priemyselné odvetvie vyrábať, potom podľa nákladových noriem môžete vypočítať priemerné priemerné koeficienty priamych nákladov v priemysle.
Po určení koeficientov aij je možné pomocou systému (4) vyriešiť vyššie uvedené problémy 1 - 3.
Technologické koeficienty majú nasledujúce vlastnosti:
HERNÉ MODELY V EKONOMIKE
1. Aké sú dôvody neistoty vo výsledkoch hry?
Rozlišujú sa tieto skupiny dôvodov vzniku neistoty a rizík z nej vyplývajúcich: neurčitosť mnohých procesov a javov, ktoré majú vplyv na ekonomiku (vedecký a technický pokrok, prírodné katastrofy, správanie konkurencie a spotrebiteľov); neúplnosť, nepresnosť a nekonzistentnosť informácií, ktoré sú spôsobené jednak technickými ťažkosťami pri získavaní a spracovaní, jednak z čisto ekonomických dôvodov - príliš vysoké náklady na získavanie informácií, ktoré presahujú možné výhody plynúce z ich držby.
nerovnaká úroveň informovanosti účastníkov trhových dohôd, napríklad predávajúcich a kupujúcich, o predmete a podmienkach dohôd (asymetria informácií); multikritériá a konflikty pri hodnotení rozhodnutí, ak je potrebné vedome robiť kompromisy, napríklad pri vytváraní systému obehu komodít treba robiť kompromisy medzi rýchlosťou spracovania objednávky a náklady na udržiavanie zásob hotových výrobkov.
2. Ako určiť dolnú a hornú cenu maticovej hry a aký je medzi nimi vzťah?
Zvážte hru m × n s maticou a určte najlepšiu stratégiu spomedzi stratégií A 1, A 2,…, A m. Pri výbere stratégie A i, hráč A musí počítať s tým, že hráč B na ňu zareaguje stratégiou B j, pre ktorú je výplata pre hráča A minimálna (hráč B sa snaží hráča „poškodiť“ A). Nech b označuje najmenšiu výplatu hráča A, keď si zvolí stratégiu A; pre všetky možné stratégie hráča B (najmenšie číslo v i-tom rade výplatnej matice). Nazvajme b nižšiu cenu hry alebo maximálnu výplatu (maximín). Toto je zaručená výplata hráča A pre akúkoľvek stratégiu hráča B. Preto
Stratégia zodpovedajúca maximínu sa nazýva stratégia maximínu. Hráč B má záujem na znížení výhier hráča A; pri voľbe stratégie B j berie do úvahy maximálny možný zisk pre A. Zavolajme B hornú cenu hry alebo minimaxovú výplatu (minimax). Toto je zaručená strata hráča B. Preto ,.
Stratégia zodpovedajúca minimaxu sa nazýva stratégia minimax. Princíp, ktorý diktuje hráčom výber tých „najopatrnejších“ stratégií minimax a maximin, sa nazýva princíp minimax. Tento princíp vyplýva z rozumného predpokladu, že každý hráč sa snaží dosiahnuť cieľ opačný k cieľu súpera. Ak sú horná a dolná cena hry rovnaká, potom sa celková hodnota hornej a dolnej ceny hry b \u003d c \u003d n nazýva čistá cena hry, alebo cena hry.
3. Sformulujte základnéveta teórie maticových hier
Hlavná veta teórie maticových hier (Neumannova veta o minime) tvrdí, že v akýchkoľvek maticových hrách existujú optimálne zmiešané stratégie x *, y *, pri ktorých sú dosiahnuteľné „minimax“ rovnaké (ich spoločnou hodnotou je hodnota hry).
Alebo Pre maticovú hru s ľubovoľnou maticou A sú hodnoty a navzájom rovnaké, t.j.
Okrem toho existuje najmenej jedna situácia v zmiešaných stratégiách, pre ktoré je vzťah k dispozícii
4. Aké sú spôsoby zjednodušenia hry?
Prvá metóda použitá na zmenšenie dimenzie matice je založená na jednom z najdôležitejších konceptov v teórii hier - tomto koncepte stratégie dominancie.
Ak je i-tý riadok po prvkoch najmenej (?) Z j-tého radu, potom sa hovorí, že i-tý rad dominuje nad j-tym riadkom. Preto hráč A nepoužíva j-tú stratégiu, pretože jeho výplata za i-tú stratégiu nie je menšia ako pri j-tej stratégii bez ohľadu na to, ako hrá hráč B. Podobne, ak je i-tý stĺpec minimálne po prvkoch ( ?) j-tého stĺpca, potom sa hovorí, že j-tý stĺpec dominuje nad i-tym stĺpcom. Preto hráč B nepoužíva i-tú stratégiu, pretože jeho strata (rovná sa zisku hráča A) s j-tou stratégiou nie je väčšia (?) Ako s i-tou stratégiou bez ohľadu na to, ako hrá hráč A. Stratégie, ostatnými stratégiami by mali byť zahodené a mali by im byť priradené nulové pravdepodobnosti. To neovplyvní cenu hry. Veľkosť hernej matice sa ale zmenší. Tu musíte začať hru riešiť. Osobitný prípad dominancie je duplikácia stratégie... Ak hracia platobná matica obsahuje niekoľko rovnakých riadkov (stĺpcov), potom z nich ponecháme iba jeden riadok a zvyšné riadky (stĺpce) zahodíme. Vyradeným stratégiám priradíme nulové pravdepodobnosti. Zjednodušenie (zmenšenie rozmeru) platobných matíc vylúčením zjavne nepriaznivých čistých stratégií je možné z nasledujúcich dôvodov Dominantné strategické vety:
Nech som byť hrou, v ktorej matici dominuje i-tá stratégia prvého hráča i + 1, a G je hra, ktorej matica sa získa z matice I vylúčením stratégie i + 1 (riadok). Potom:
1. cena hry I sa rovná cene hry G;
2. optimálna zmiešaná stratégia Q * \u003d (q 1 *, q 2 *,…, q n *) druhého hráča v hre G je zároveň jeho optimálnou zmiešanou stratégiou v hre I;
3. ak P * \u003d (p 1 *, p 2 *,…, pi *, p * i + 2,…, pm *) je optimálna zmiešaná stratégia prvého hráča v hre G, potom jeho zmiešaná stratégia P * \u003d (p 1 *, p 2 *,…, pi *, p * i + 2,…, pm *) je optimálne v hre I.
Z vyššie uvedeného vyplýva, že nemá zmysel, aby prvý aj druhý používali dominovanú stratégiu, preto môžu byť všetky dominujúce stratégie zahodené, t. v skutočnosti sú riadky a stĺpce pôvodnej matice A zodpovedajúce týmto riadkom zahodené. Táto transformácia zmenšuje rozmer pôvodnej platobnej matice A, čím zjednodušuje hľadanie optimálneho riešenia.
5. Geometrické metódy riešenia hier s 2_ maticami_nam 2 a ich uplatňovanie
Riešenie hry v zmiešaných stratégiách umožňuje jasnú geometrickú interpretáciu. Geometrická metóda riešenia hry obsahuje nasledujúce etapy. 1. V karteziánskom súradnicovom systéme pozdĺž úsečky je vynesený segment A1A2, ktorého dĺžka je 1 (obr. 2.1.). Ľavý koniec segmentu, bod x \u003d 0, zodpovedá stratégii A1, pravý koniec, kde x \u003d 1,0 - stratégia A2. Všetky medziľahlé body tohto segmentu zodpovedajú zmiešaným stratégiám S1 \u003d (p1, p2). 2. Na osi y od bodu O sú výhry zakreslené pre stratégiu A1. 3. Na priamke rovnobežnej s osou súradníc sa od bodu 1 vkladajú výhry pre stratégiu A2. Nech existuje hra s výplatnou maticou:
Ak hráč II použije stratégiu B1, potom sa vyplatí hráčovi I pri použití čistých stratégií A1 a A2 a11 \u003d 0,4 a a21 \u003d 0,6. Spojme tieto body priamkou В1В1. Ak hráč I so stratégiou B1 použije zmiešanú stratégiu, potom je priemerná odmena určená vzorcom matematického očakávania g1 \u003d a11p1 + a21p2 predstavovaná súradnicou bodu N na priamke B1B1. Priamka B1B1 sa nazýva stratégia B1. Súradnica ktoréhokoľvek bodu segmentu B1B1 sa rovná hodnote výplaty hráča I, keď uplatňuje stratégie A1 a A2 so zodpovedajúcimi pravdepodobnosťami p1 a p2. Podobne konštruujeme segment B2B2 zodpovedajúci uplatneniu stratégie B2 hráčom II. Súradnice bodov segmentu určujú priemer stratégií A1 a A2 so zodpovedajúcimi pravdepodobnosťami p1 a p2 a rovná sa g2 \u003d a12p1 + a22p2.
6. Na čom je založené spojenie medzi maticovou hrou a problémom lineárneho programovania?
Vývoj teórie hier strategickej matice sa spočiatku realizoval paralelne a nezávisle od lineárneho programovania. Neskôr sa zistilo, že strategická maticová hra sa dá redukovať na dvojicu problémov s duálnym lineárnym programovaním. Po vyriešení jedného z nich získame optimálne stratégie hráča 1; Riešením druhého získame optimálne stratégie hráča 2. Matematickú korešpondenciu medzi hrami strategickej matice a lineárnym programovaním vytvoril JB Danzig, ktorý sformuloval a v roku 1951 sformuloval hlavnú vetu teórie hier.
Veta. Každá maticová hra s nulovým súčtom má vždy zmiešané strategické riešenie, t.j. existuje číslo v a stratégie U * a W * hráčov 1 a 2, ktoré zodpovedajú nasledujúcim nerovnostiam:
Ujasnime si význam dokázaných nerovností: ak sa hráč 1 odchýli od svojej optimálnej stratégie, jeho výplata sa v porovnaní s cenou hry nezvýši; ak sa hráč 2 odchýli od svojej optimálnej stratégie, jeho strata sa v porovnaní s cenou hry neznižuje.
7. Aký je rozdiel medzi hraním sa s prírodou?
Charakteristickým rysom hry s prírodou je, že v nej vedome koná iba jeden z účastníkov, ktorý sa vo väčšine prípadov nazýva hráč 1. Hráč 2 (príroda) zámerne nekoná proti hráčovi 1, ale chová sa tak, že nemá konkrétny cieľ a náhodne vyberie ďalší „Presúva“ partnera v hre. Preto pojem „príroda“ charakterizuje určitú objektívnu realitu, ktorú by sa nemalo brať doslovne, aj keď môžu nastať situácie, v ktorých môže byť príroda skutočne „hráčom“ 2 (napríklad okolnosti súvisiace s poveternostnými podmienkami alebo prírodnými silami prírody).
8. Vymenujte hlavné kritériá riešenia hier s prírodou a aké sú vzorce výpočtu pre tieto kritériá.
Bayesovo kritérium.
Podľa Bayesovho kritéria je optimálnou stratégiou stratégia (čistá) A i, ktorá maximalizuje priemernú výplatu a alebo minimalizuje priemerné riziko r.
Počítame hodnoty? (A ij p j)
Laplaceovo kritérium.
Ak sú pravdepodobnosti prírodných stavov pravdepodobné, používajú Laplaceov princíp nedostatočného základu, podľa ktorého sa všetky prírodné stavy považujú za rovnako pravdepodobné, t. J .:
q 1 \u003d q 2 \u003d ... \u003d q n \u003d 1 / n.
Waldove kritérium.
Podľa Waldovho kritéria sa za optimálnu stratégiu považuje čistá stratégia, ktorá zaručuje maximálny zisk v najhorších podmienkach, t.
a \u003d max (min a ij)
Waldovo kritérium orientuje štatistiku na najnepriaznivejšie podmienky prírody, t. toto kritérium vyjadruje pesimistické hodnotenie situácie.
Savageove kritérium.
a \u003d min (max r ij)
Savageove kritérium orientuje štatistiku na najnepriaznivejšie podmienky prírody, t.j. toto kritérium vyjadruje pesimistické hodnotenie situácie.
Hurwitzovo kritérium.
Hurwitzovo kritérium je kritériom pre pesimizmus - optimizmus. Pre (optimálna stratégia je tá, pre ktorú je vzťah splnený:
kde s i \u003d y min (a ij) + (1-y) max (a ij)
Pre y \u003d 1 dostaneme Waldeho kritérium, pre y \u003d 0 dostaneme optimistické kritérium (maximax).
Hurwitzovo kritérium zohľadňuje možnosť najhoršieho a najlepšieho správania sa človeka v prírode. Ako je vybraté? Čím horšie sú následky chybných rozhodnutí, tým väčšia je túžba poistiť sa proti chybám, tým bližšie je y k 1.
Kritérium Maximax.
Kritérium maximax orientuje štatistiku na najpriaznivejšie prírodné podmienky, t. toto kritérium vyjadruje optimistické hodnotenie situácie.
Praktické úlohy
Úloha číslo 1
Vyriešime problém priameho lineárneho programovania pomocou simplexovej metódy pomocou simplexovej tabuľky.
Určte maximálnu hodnotu objektívnej funkcie F (X) \u003d 2x 1 + 5x 2 + 6x 3 za nasledujúcich podmienok obmedzenia.
7x 1 + 8x 2 + 3x 3? 81
4x 1 + x 2 + 6x 3? 68
5x 1 + x 2 + 7x 3? 54
Pri zostavovaní prvého referenčného plánu sa systém nerovností redukuje na systém rovníc zavedením ďalších premenných (prechod do kanonickej formy).
V 1. význame nerovnosť (?) Predstavíme základnú premennú x 4. V druhej významovej nerovnosti (?) Si predstavíme základnú premennú x 5. V 3. významovej nerovnosti (?) Uvedieme základnú premennú x 6.
7x 1 + 8x 2 + 3x 3 + 1x 4 + 0x 5 + 0x 6 \u003d 81
4x 1 + 1x 2 + 6x 3 + 0x 4 + 1x 5 + 0x 6 \u003d 68
5x 1 + 1x 2 + 7x 3 + 0x 4 + 0x 5 + 1x 6 \u003d 54
Matica koeficientu A \u003d a (ij) tohto systému rovníc má tvar:
Základné premenné sú premenné, ktoré sú obsiahnuté iba v jednej rovnici systému obmedzení a navyše s jednotkovým koeficientom.
Ekonomický význam ďalších premenných: ďalšie zmeny v úlohe LP označujú prebytočné suroviny, čas a ďalšie zdroje zostávajúce pri príprave daného optimálneho plánu.
Vyriešime sústavu rovníc pre základné premenné: x 4, x 5, x 6
Za predpokladu, že voľné premenné sú 0, dostaneme prvú základňu:
X1 \u003d (0,0,0,81,68,54)
Základné riešenie sa nazýva prípustné, ak je nezáporné.
Prejdime k základnému algoritmu simplexovej metódy.
Iterácia # 0.
1. Kontrola kritéria optimality.
Aktuálny referenčný plán nie je optimálny, pretože v riadku indexu sú negatívne kurzy.
2. Definícia novej bázickej premennej.
Ako úvodný zvolíme stĺpec zodpovedajúci premennej x 3, pretože ide o najväčší koeficient v module.
...Podobné dokumenty
Matematická formulácia problému lineárneho programovania. Aplikácia simplexnej metódy na riešenie problémov. Geometrická interpretácia problému lineárneho programovania. Aplikácia metód lineárneho programovania na extrémne ekonomické problémy.
semestrálna práca pridaná 5. 5. 2014
Nájdenie rozsahu prípustných hodnôt a optimálnych hodnôt cieľovej funkcie za účelom riešenia problému lineárneho programovania grafickou metódou. Nájdenie optimálnych hodnôt duálnych premenných pomocou simplexnej metódy a teórie duality.
test, pridané 04/09/2012
Riešenie úlohy lineárneho programovania grafickým spôsobom. Určenie krajného bodu. Kontrola optimality plánu. Pravidlo obdĺžnikov. Analýza a oprava výsledkov riešenia problémov lineárneho programovania pomocou simplexnej metódy.
test, pridané 5. 4. 2014
Simplexná metóda riešenia problémov lineárneho programovania. Prvky teórie hier. Systémy hromadného radenia. Problém s dopravou. Graficko-analytická metóda na riešenie problémov lineárneho programovania. Stanovenie optimálnej stratégie podľa Waldeho kritéria.
test, pridané 24. 8. 2010
História vzniku digitálnej výpočtovej technológie. Metódy a modely lineárneho programovania. Ekonomické vyjadrenie problému. Voľba metódy implementácie problému. Vlastnosti výberu programovacieho jazyka. Riešenie problému metódou sieťového plánovania.
seminárna práca pridaná 19. 2. 2015
Koncept matematického programovania ako odvetvia matematiky, ktorý je teoretickým základom pre riešenie problémov hľadania optimálnych riešení. Hlavné fázy hľadania optimálneho riešenia ekonomických problémov. Príklady problémov lineárneho programovania.
tutoriál pridaný 15. júna 2015
Modelovanie ekonomických systémov: základné pojmy a definície. Matematické modely a metódy ich výpočtu. Niekoľko informácií z matematiky. Príklady problémov lineárneho programovania. Metódy riešenia problémov lineárneho programovania.
prednáška pridaná 15. 6. 2004
Ekonomický a matematický model na získanie maximálneho zisku, jeho riešenie grafickou metódou. Algoritmus riešenia problému lineárneho programovania pomocou simplexnej metódy. Zostavenie duálneho problému a jeho grafické riešenie. Riešenie platobnej matice.
test, pridané 05/11/2014
Grafické riešenie problémov lineárneho programovania. Riešenie problémov lineárneho programovania pomocou simplexnej metódy. Možnosti praktického využitia matematického programovania a ekonomických a matematických metód pri riešení ekonomických problémov.
semestrálna práca, pridané 2. 2. 2014
Základné pojmy modelovania. Všeobecné pojmy a definícia modelu. Vyhlásenie o optimalizačných problémoch. Metódy lineárneho programovania. Všeobecná a typická úloha v lineárnom programovaní. Simplexná metóda riešenia problémov lineárneho programovania.
MINISTERSTVO POĽNOHOSPODÁRSTVA RUSKEJ FEDERÁCIE
Katedra štatistiky
a informačné systémy
v ekonomike
B2.B4 metódy optimálnych riešení
Pokyny pre disciplínu
Smer školenia 080100 Ekonomika
Poskytovanie profilov
Financie a úvery
Dane a dane
Účtovníctvo, analýza a audit
Ekonomika podnikov a organizácií
Kvalifikácia (titul) absolventa
Bakalár
Zostavil: starší učiteľ Sagadeeva E.F.
Recenzent: kandidát sociálnych vied, docent na katedre matematiky Gilmanova G. Kh.
Zodpovedný za prepustenie: hlava. Katedra štatistiky a informačných systémov v ekonómii, kandidát ekonomických vied, docent A. Ableeva
|
Úvod | |
|
1. Geometrická interpretácia problémov lineárneho programovania | |
|
2. Zjednodušená metóda riešenia problému lineárneho programovania | |
|
3. Základné pojmy teórie duality | |
|
4 metóda dual simplex | |
|
5. Simplexná metóda na umelom základe | |
|
6. Programovanie celých čísel. Gomoriho metóda | |
|
7. Frakčné lineárne programovanie | |
|
8. Problémy nelineárneho programovania. Lagrangeova multiplikačná metóda | |
|
9. Úlohy pre samostatnú prácu | |
|
10. Testovacie úlohy | |
|
11. Úlohy na vykonávanie výpočtových a grafických prác a kontrolných prác študentov korešpondencie | |
|
12. Fond testových otázok | |
|
13. Vstupenky na skúšku | |
|
14. Bibliografia |
Úvod
Optimálne rozhodovacie metódy sú odbor matematiky, ktorý študuje teóriu a metódy hľadania najlepších možností plánovania ľudských ekonomických aktivít v jednom konkrétnom podniku, v určitom priemysle alebo v konkrétnom regióne alebo v celom štáte.
Najlepšie možnosti sú také, ktoré dosahujú maximálnu produktivitu práce, minimálne náklady, maximálny zisk, minimálne využitie zdrojov atď. Z hľadiska matematiky ide o triedu optimalizačných problémov. Hlavným nástrojom na ich riešenie je matematické modelovanie. Matematický model je formálny popis skúmaného javu a „preklad“ všetkých existujúcich informácií o ňom do jazyka matematiky vo forme rovníc, identít a nerovností. Ak sú všetky tieto vzťahy lineárne, potom sa celý problém nazýva problém lineárneho programovania (LPP). Kritériom efektívnosti tohto modelu je určitá funkcia, ktorá sa nazýva cieľová funkcia.
Poďme formulovať všeobecný problém lineárneho programovania.
Nech je daný systém m lineárne rovnice a nerovnosti s n premenné (systém obmedzení):
 (1)
(1)
a lineárna funkcia
Je potrebné nájsť riešenie systému (1), v ktorom lineárna funkcia berie maximálnu (minimálnu) hodnotu.
Všeobecne môže mať LPP nekonečné množstvo riešení. Často sa nazýva riešenie vyhovujúce obmedzeniam (1) plán... Ak sú všetky komponenty (3) určené pre toner prijateľné rozhodnutie.
Optimálne riešenie alebo optimálny plán úlohy lineárneho programovania sa nazýva riešenie, ktoré spĺňa všetky obmedzenia systému (1), podmienky (3) a súčasne dáva maximum (minimum) objektívnej funkcie (2).
|
Kanonické |
Štandardné |
Všeobecné |
|
1) Obmedzenia |
||
|
Rovnice |
Nerovnosti |
Rovnice a nerovnosti |
|
2) Podmienky týkajúce sa negativity |
||
|
Všetky premenné |
Všetky premenné |
Časť premenných |
|
3) Objektívna funkcia |
||
|
(maxalebo min) |
||
Tu: - premenné problému; - koeficienty premenných v objektívnej funkcii; - koeficienty premenných v hlavných obmedzeniach problému; - pravá strana obmedzení.
Lineárne programovanie - je veda o metódach výskumu a hľadaní najväčších a najmenších hodnôt lineárnej funkcie, ktorých neznáma je lineárne obmedzená. Problémy s lineárnym programovaním teda súvisia s problémami pre podmienený extrém funkcie. Zdá sa, že na štúdium lineárnej funkcie mnohých premenných pre podmienený extrém stačí použiť dobre vyvinuté metódy matematickej analýzy, ale nemožnosť ich použitia možno celkom jednoducho ilustrovať.
Dráhu treba skutočne preskúmať kvôli extrému lineárnej funkcie
Z \u003d C 1 x 1 + C 2 x 2 + ... + C N x N
s lineárnymi obmedzeniami
a 11 x 1 + a 22 x 2 + ... + a 1 N X N \u003d b 1
a 21 x 1 + a 22 x 2 + ... + a 2N X N \u003d b 2
. . . . . . . . . . . . . . .
a M 1 x 1 + a M 2 x 2 + ... + a M N X N \u003d b M
Pretože Z je lineárna funkcia, potom Z \u003d Сj, (j \u003d 1, 2, ..., n), potom sa všetky koeficienty lineárnej funkcie nemôžu rovnať nule, preto vo vnútri oblasti tvorenej systémom obmedzení nie sú krajné body existuje. Môžu byť na hranici oblasti, ale nie je možné skúmať body hranice, pretože čiastkové derivácie sú konštanty.
Na riešenie problémov lineárneho programovania bolo potrebné vytvoriť špeciálne metódy. Lineárne programovanie je obzvlášť rozšírené v ekonómii, pretože štúdium závislostí medzi veličinami nachádzajúcimi sa v mnohých ekonomických problémoch vedie k lineárnej funkcii s lineárnymi obmedzeniami uvalenými na neznáme.
V súčasnosti vzdelávací program špecializácií z ekonómie, financií a manažmentu obsahuje disciplínu nazvanú „Metódy optimálneho rozhodovania“. V tejto disciplíne študenti študujú matematickú stránku optimalizácie, operačného výskumu, rozhodovania a modelovania. Hlavný rys tejto disciplíny je určený spoločným štúdiom matematických metód s ich aplikáciou na riešenie ekonomických problémov.
Optimalizačné úlohy: všeobecné informácie
Ak vezmeme do úvahy všeobecný prípad, potom zmyslom problému s optimalizáciou je nájsť takzvané optimálne riešenie, ktoré za určitých podmienok-obmedzení maximalizuje (minimalizuje) objektívnu funkciu.
V závislosti na vlastnostiach funkcií možno problémy s optimalizáciou rozdeliť na dva typy:
- problém lineárneho programovania (všetky funkcie sú lineárne);
- nelineárny problém s programovaním (aspoň jedna z funkcií nie je lineárna).
Konkrétnymi prípadmi optimalizačných problémov sú lineárne-zlomkové, dynamické a stochastické programovacie problémy.
Najštudovanejšími optimalizačnými problémami sú problémy s lineárnym programovaním (LPP), ktorých riešenie berie iba celočíselné hodnoty.
ZLP: formulácia, klasifikácia
Všeobecným problémom lineárneho programovania je nájsť minimum (maximum) lineárnej funkcie za určitých lineárnych obmedzení.
Všeobecný LPP sa nazýva problém formulára

s obmedzeniami

kde sú premenné, sú dané skutočné čísla, je objektívna funkcia, je plán úloh, (*) - (***) sú obmedzenia.
Dôležitou vlastnosťou LPP je, že extrém objektívnej funkcie sa dosahuje na hranici oblasti uskutočniteľných riešení.
Metódy optimálneho riešenia nachádzajú praktické ekonomické uplatnenie pri riešení problémov nasledujúcich typov:
- zmiešané úlohy (t. j. plánovanie zloženia produktu);
- problém optimálneho rozdelenia zdrojov pri plánovaní výroby;
ZLP: príklady
Problém so zmesou
Riešenie problému zmesí spočíva v nájdení najlacnejšej súpravy pozostávajúcej z určitých východiskových materiálov, ktoré poskytujú zmesi s požadovanými vlastnosťami.
Problém s alokáciou zdrojov
Podnik vyrába n rôzne výrobky, na výrobu ktorých sa vyžaduje m rôzne druhy zdrojov. Rezervy na použité zdroje sú obmedzené a zodpovedajúcim spôsobom zodpovedajú výške b 1, b 2,…, b m cu Okrem toho sú známe technologické koeficienty a ijktoré ukazujú, koľko jednotiek i-tý zdroj je potrebný na výrobu jednej jednotky produktu j-ty druh (). Zisk, ktorý spoločnosť získa z predaja produktu j-th druh je c j peňažné jednotky Je potrebné vypracovať plán na uvedenie výrobkov na trh, ktorých zisk podniku pri realizácii bude najväčší.
Podmienky zmiešania a problémy s alokáciou zdrojov sú často napísané v tabuľkovej forme.
| Zdroje | Potreby | Zásoby | ||
| B 1 | … | B n | ||
| A 1 | b 1 | |||
| … | … | |||
| A m | b m | |||
| Zisk | c 1 | … | c n | |
Problémy s miešaním a alokáciou zdrojov je možné vyriešiť niekoľkými spôsobmi:
- grafická metóda (v prípade malého počtu premenných v matematickom modeli);
- simplexová metóda (ak je počet premenných v matematickom modeli viac ako dva).
Transportná úloha je trieda úloh, ktoré majú určitú špecifickú štruktúru. Najjednoduchším problémom pri preprave je problém s prepravou produktu do cieľových miest z východiskového miesta pri najnižších nákladoch na prepravu všetkých produktov.
Pre prehľadnosť a pohodlie vnímania je stav problému s dopravou zvyčajne napísaný v tabuľke v tejto podobe:

Všeobecne sa riešenie dopravného problému uskutočňuje v niekoľkých etapách:
- Fáza I: príprava pôvodného referenčného plánu;
- Fáza II: kontrola optimality základného plánu;
- Fáza III: objasnenie referenčného plánu, ak nie je optimálny.
Existuje niekoľko metód na získanie počiatočného základného plánu, napríklad metóda Northwest Corner, metóda Vogel a metóda nízkych nákladov.
Optimálnosť plánu sa kontroluje pomocou potenciálnej metódy:
- pre obsadené bunky,
- pre neobsadené bunky.
Ak plán nie je optimálny, vykoná sa budovanie cyklu a prerozdelenie dopravy.
Záver
V rámci jedného článku nie je možné pokryť celú teóriu a prax metód optimálneho riešenia, preto sa uvažuje iba s niektorými bodmi, ktoré umožňujú poskytnúť všeobecnú predstavu o tejto disciplíne, problémoch a metódach ich riešenia.
Okrem toho je dobré poznamenať, že na kontrolu získaných riešení problémov s optimalizáciou môžete veľmi efektívne použiť doplnok „Vyhľadať riešenie“ v programe MS Excel. Ale toto je v skutočnosti iný príbeh, ako aj podrobné zváženie metód riešenia problémov s optimalizáciou.
Tu je niekoľko návodov na osvojenie si metód optimálneho riešenia:
- Bundy B. Základy lineárneho programovania: Per. z angličtiny. - M.: Rádio a komunikácia, 1989. - 176 s.
- Kremer N.Sh. Operačný výskum v ekonómii: učebnica. príručka pre univerzity / N. Sh. Kremer, BA. Putko, I.M. Trishin, M.N. Friedman; Ed. prof. N.Sh. Kremer. - M.: UNITI, 2005. - 407 s.
Riešenie optimalizačných metód na zákazku
S riešením každého problému vám môžeme pomôcť metódami optimálneho riešenia. Riešenie problémov si môžete objednať na našom webe. Všetko, čo musíte urobiť, je označiť termín a priložiť súbor s úlohou. Vaša objednávka je zadarmo.
Optimálne metódy rozhodovania
OBSAH
Hlavnými ustanoveniami disciplíny „Metódy optimálnych riešení“ sú základ matematického vzdelávania absolventa, ktorý je dôležitý pre úspešné štúdium špeciálnych odborov, ktoré zabezpečuje hlavný vzdelávací program pre túto špecializáciu.
Pre efektívnu asimiláciu vzdelávacieho materiálu a získanie záverečnej certifikácie je potrebné v čase stanovenom učebnými osnovami splniť kontrolné úlohy a poskytnúť ich na overenie učiteľovi e-mailom. Harmonogram štúdia a podávania správ podľa disciplín je uvedený v tabuľke 1.
Tabuľka 1. Harmonogram samostatnej práce v disciplíne „Metódy optimálneho rozhodovania“
| Obsah | Termín dodania | Kritériá hodnotenia |
| 1. Preskúmanie teoretického materiálu | ||
| 2. Riešenie úloh kontrolnej práce | 1,5 mesiaca pred zasadnutím | Každá úloha je hodnotená na desaťbodovom systéme |
| 3. Príprava na záverečné attsídliská | Počas relácie |
1. ÚVOD. VŠEOBECNÉ VYHLÁSENIE O PROBLÉME
Rozhodovacie procesy sú jadrom každej cieľavedomej činnosti. V ekonomike predchádzajú vzniku priemyselných a hospodárskych organizácií, zabezpečujú ich optimálne fungovanie a interakciu. Vo vedeckom výskume - umožňujú zvýrazniť najdôležitejšie vedecké problémy, nájsť spôsoby, ako ich študovať, predurčiť vývoj experimentálnej bázy a teoretického aparátu. Pri vytváraní nových technológií tvoria dôležitú etapu v konštrukcii strojov, prístrojov, zariadení, komplexov, budov, vo vývoji technológií na ich stavbu a prevádzku; v sociálnej sfére - slúžia na organizáciu fungovania a rozvoja sociálnych procesov, ich koordináciu s ekonomickými a ekonomickými procesmi. Optimálne (efektívne) riešenia vám umožňujú dosiahnuť vaše ciele s minimálnymi nákladmi na prácu, materiál a suroviny.
V klasickej matematike sa metódam hľadania optimálnych riešení venujeme v častiach týkajúcich sa štúdia extrémov funkcií v matematickom programovaní.
Optimálne metódy rozhodovania sú jedným z odvetví operačného výskumu - aplikovaným smerom kybernetiky používaným na riešenie praktických organizačných problémov. Problémy matematického programovania sa využívajú v rôznych oblastiach ľudskej činnosti, kde je potrebné zvoliť jeden z možných spôsobov konania (akčné programy).
Významné množstvo úloh, ktoré v spoločnosti vznikajú, súvisí s kontrolovanými javmi, to znamená s javmi regulovanými na základe vedome prijímaných rozhodnutí. S obmedzeným množstvom informácií, ktoré boli k dispozícii v raných fázach vývoja spoločnosti, bolo urobené optimálne rozhodnutie založené na intuícii a skúsenostiach, a potom so zvýšením množstva informácií o skúmanom jave pomocou série priamych výpočtov. Stalo sa tak napríklad pri tvorbe harmonogramov práce priemyselných podnikov.
Úplne iný obraz vzniká napríklad v modernom priemyselnom podniku s viacdávkovou a viacproduktovou výrobou, keď je objem vstupných informácií taký veľký, že ich spracovanie za účelom určitého rozhodnutia je nemožné bez použitia moderných elektronických počítačov. Ešte väčšie ťažkosti vznikajú v súvislosti s problémom najlepšieho rozhodnutia.
Rozhodovanie v kurze „Metódy optimálneho rozhodovania“ sa chápe ako komplexný proces, v ktorom možno rozlíšiť tieto hlavné etapy:
1. etapa. Budovanie kvalitatívneho modelu posudzovaného problému, to znamená identifikácia faktorov, ktoré sa javia ako najdôležitejšie, a stanovenie vzorcov, ktorým sa podriaďujú. Zvyčajne táto fáza presahuje rámec matematiky.
2. etapa. Vytvorenie matematického modelu uvažovaného problému, to znamená napísanie kvalitatívneho modelu v matematickej rovine. Matematický model je teda abstrakciou skutočného javu napísanou v matematických symboloch, takže jeho analýza umožňuje preniknúť do podstaty javu. Matematický model ustanovuje vzťahy medzi množinou premenných - parametrami riadenia javu. Táto etapa zahŕňa aj zostavenie objektívnej funkcie premenných, to znamená takej numerickej charakteristiky, ktorej vyššia (alebo nižšia) hodnota zodpovedá najlepšej situácii z hľadiska rozhodnutia.
Výsledkom týchto dvoch stupňov je, že sa vytvorí zodpovedajúci matematický problém. Druhá etapa si už navyše vyžaduje zapojenie matematických znalostí.
3. etapa. Štúdium vplyvu premenných na hodnotu objektívnej funkcie. Táto fáza poskytuje vlastníctvo matematického aparátu na riešenie matematických problémov, ktoré vzniknú v druhej etape rozhodovacieho procesu.
Širokú triedu kontrolných problémov tvoria také extrémne problémy, v ktorých matematických modeloch sú podmienky v premenných špecifikované rovnosťami a nerovnosťami. Teória a metódy riešenia týchto problémov sú presne obsahom matematického programovania. V tretej etape pomocou matematického aparátu nájdu riešenie zodpovedajúcich extrémnych problémov. Venujme pozornosť skutočnosti, že problémy matematického programovania spojené s riešením praktických problémov majú spravidla veľké množstvo premenných a obmedzení. Množstvo výpočtovej práce na nájdenie vhodných riešení je také veľké, že celý proces nie je možné koncipovať bez použitia moderných elektronických počítačov (počítačov), čo znamená, že si vyžaduje buď vytvorenie počítačových programov, ktoré implementujú určité algoritmy, alebo použitie existujúcich štandardných programov.
4. etapa. Porovnanie výsledkov výpočtu získaných v 3. etape s modelovaným objektom, t. J. Odborné overenie výsledkov (praktické kritérium). V tejto fáze je teda stupeň presnosti modelu a modelovaného objektu stanovený v rámci presnosti počiatočných informácií. Tu sú možné dva prípady:
1. prípad. Ak sú výsledky porovnania neuspokojivé (bežná situácia v počiatočnej fáze procesu modelovania), pokračujte druhým cyklom procesu. Zároveň sa špecifikujú vstupné informácie o modelovanom objekte a v prípade potreby sa špecifikuje formulácia problému (1. etapa); matematický model je zdokonalený alebo prestavaný (2. etapa); príslušná matematická úloha je vyriešená (fáza 3) a nakoniec sa porovnanie uskutoční znova (fáza 4).
2. prípad. Ak sú výsledky zhody uspokojivé, model sa prijme. Pokiaľ ide o opakované použitie výsledkov výpočtov v praxi, nastáva problém s prípravou modelu na prevádzku. Predpokladajme napríklad, že účelom simulácie je vytvorenie výrobných plánov pre podnik. Potom prevádzka modelu zahŕňa zber a spracovanie informácií, vkladanie spracovaných informácií do počítača, výpočty na základe vypracovaných rozvrhových programov a nakoniec vydávanie výsledkov výpočtov (vo forme vhodnej pre používateľov) pre ich použitie v oblasti výrobných činností.
V matematickom programovaní existujú dva smery.
Prvý, už úplne zavedený smer - správne matematické programovanie - obsahuje deterministické problémy za predpokladu, že všetky počiatočné informácie sú úplne definované.
Druhý smer - takzvané stochastické programovanie - obsahuje problémy, v ktorých počiatočné informácie obsahujú prvky neistoty, alebo keď sú niektoré parametre problému náhodnej povahy so známymi pravdepodobnostnými charakteristikami. Plánovanie výrobných činností sa tak často vykonáva v podmienkach neúplných informácií o skutočnej situácii, v ktorej bude plán vykonaný. Alebo povedzme, keď extrémny problém simuluje činnosť automatických zariadení, ktorá je sprevádzaná náhodným rušením. Všimnite si, že jedna z hlavných ťažkostí stochastického programovania spočíva v samotnej formulácii problémov, hlavne kvôli zložitosti analýzy počiatočných informácií.
V matematickom programovaní sa tradične rozlišujú tieto hlavné časti:
Lineárne programovanie - objektívna funkcia je lineárna a množinu, na ktorej sa hľadá extrém objektívnej funkcie, definuje systém lineárnych rovností a nerovností. Na druhej strane v lineárnom programovaní existujú triedy problémov, ktorých štruktúra umožňuje vytvárať špeciálne metódy ich riešenia, ktoré sa priaznivo líšia od metód riešenia všeobecných problémov. Tak sa v lineárnom programovaní objavila časť dopravných problémov.
Nelineárne programovanie - objektívna funkcia a obmedzenia sú nelineárne. Nelineárne programovanie sa zvyčajne člení takto:
Konvexné programovanie - objektívna funkcia je konvexná (ak sa uvažuje o probléme jej minimalizácie) a konvexná množina, na ktorej je extrémny problém vyriešený.
Kvadratické programovanie - cieľová funkcia je kvadratická a obmedzeniami sú lineárne rovnosti a nerovnosti.
Multi-extrémne úlohy. Zvyčajne sa tu rozlišujú špecializované triedy problémov, s ktorými sa v aplikáciách často stretávame, napríklad problémy s minimalizáciou na konvexnej množine konkávnych funkcií.
Dôležitou časťou matematického programovania je celočíselné programovanie, keď sú na premenné kladené celočíselné podmienky.
Cieľom matematického programovania je vytvoriť, pokiaľ je to možné, analytické metódy na určenie riešenia a pri ich absencii vytvoriť efektívne výpočtové metódy na získanie približného riešenia.
Na záver poznamenávame, že názov predmetu - „metódy optimálnych riešení“ - je spojený so skutočnosťou, že cieľom riešenia problémov je zvoliť program činnosti. Uvažujme podrobnejšie o probléme lineárneho programovania
2. GEOMETRICKÁ INTERPRETÁCIA PROGRAMU LINEÁRNEHO PROGRAMOVANIA
Problém s lineárnym programovaním (LPP):
nájdite vektor X \u003d (x 1, x 2, ..., x n) maximalizujúci lineárny tvar
F \u003d Σ c j x j → max (2,1)
J \u003d 1
a splnenie podmienok:
Σa ij x j ≤ b i (2.2)
J \u003d 1
x j ≥0, j \u003d 1, ..., n (2,3)
Lineárna funkcia F sa nazýva objektívna funkcia úlohy.
Prepíšme tento problém vo vektorovej podobe:
Poďme nájsť funkciu max:
F \u003d c 1 x 1 + c 2 x 2 + ... + c n x n (2,4)
x 1 P 1 + x 2 P 2 +… + x n P n \u003d P 0, (2,5)
x j ≥0, j \u003d 1, ..., n (2,6)
kde P 1, ..., P n a P 0 - m-rozmerné vektorové stĺpce, z koeficientov pri neznámych a voľných podmienkach systému rovníc úlohy:
B 1 a 11 a 12 a 1 n
PO \u003d (b2); Pl \u003d (a 21); P 2 \u003d (a 22); ……. Pn \u003d (a 2n); (2,7)
… … … …
B n a m1 a m2 a mn
Plán X \u003d (x 1, x 2, ..., x n) sa nazýva základný plán hlavného LPP, ak kladné koeficienty x j znamenajú lineárne nezávislé vektory P j.
Akákoľvek neprázdna sada plánov základného problému lineárneho programovania sa nazýva polytop riešenia a akýkoľvek rohový bod polytopu riešenia sa nazýva vrchol.
Veta
Ak má hlavný LPP optimálny plán, objektívna funkcia problému nadobúda maximálnu hodnotu na jednom z vrcholov rozhodovacieho mnohostenu.
Ak objektívna funkcia úlohy nadobúda maximálnu hodnotu na viac ako jednom vrchole, potom ju berie v ktoromkoľvek bode, ktorý je konvexnou lineárnou kombináciou týchto vrcholov.
Závery:
Neprázdna sada plánov základného LPP tvorí konvexný mnohosten;
Každý vrchol tohto mnohostena definuje referenčný plán;
Na jednom z vrcholov mnohostena je hodnota objektívnej funkcie maximálna.
Dvojrozmerný prípad ZLP
Nájdeme riešenie problému, ktorý spočíva v určení maximálnej hodnoty funkcie
F \u003d c 1 x 1 + c 2 x 2 (2,8)
za podmienok
a i1 x 1 + a i2 x 2 ≤ b i, (i \u003d 1, ..., k) (2,9)
x j ≥0 (j \u003d 1,2) (2,10)
Úlohou lineárneho programovania je nájsť bod polygónu riešenia, v ktorom cieľová funkcia F nadobúda svoju maximálnu hodnotu. Tento bod existuje, keď polygón riešenia nie je prázdny a objektívna funkcia je na ňom zhora ohraničená.
Aby sme určili tento vrchol, zostrojíme rovinnú priamku c 1 x 1 + c 2 x 2 \u003d h, (kde h je nejaká konštanta) prechádzajúcu cez polygón riešenia, a budeme ju posúvať v smere vektora C \u003d (c 1, c 2), kým kým neprejde svojím posledným spoločným bodom s polygónom riešenia. Súradnice zadaného bodu určujú optimálny plán pre túto úlohu.
Fázy riešenia LPP geometrickou metódou:
1. Zostrojte priame čiary podľa rovníc (2.9), (2.10).
2. Nájdite polroviny definované každou z obmedzení úlohy.
3. Nájdite riešenia mnohouholníkov.
4. Zostrojte vektor C.
5. Zostrojte priamku c 1 x 1 + c 2 x 2 \u003d h prechádzajúcu polygónom riešenia.
6. Posuňte priamku c 1 x 1 + c 2 x 2 \u003d h v smere vektora C.
7. Určte súradnice maximálneho bodu funkcie a vypočítajte hodnotu objektívnej funkcie v tomto bode.
Príklad 1.
Na výrobu dvoch druhov výrobkov A a B používa spoločnosť tri druhy surovín. Miera spotreby každého druhu suroviny na výrobu jednotky tohto typu výrobku je uvedená v tabuľke 2.1. Označuje tiež zisk z predaja jedného produktu každého druhu a celkové množstvo surovín tohto typu, ktoré môže podnik použiť.
Tabuľka 2.1
| INidy suroviny | Miera spotreby surovín (kg) pre jeden výrobok | Celkové množstvo surovín (kg) |
|
| A | IN |
||
| 1 | 12 | 4 | 300 |
| 2 | 4 | 4 | 120 |
| 3 | 3 | 12 | 252 |
| Zisk z predaja jedného produktu (RUB) | 30 | 40 | |
Vzhľadom na to, že produkty A a B sa dajú vyrobiť v akomkoľvek pomere
niyah (predaj zabezpečený), je potrebné vypracovať taký plán ich prepustenia, keďzisk podniku z predaja všetkých výrobkov je maximálnymalý.Rozhodnutie:
х1 - výroba výrobkov typu A.
х2 - výroba výrobkov typu B.
Obmedzenia problému sú:
Celkový zisk z predaja výrobkov typu A a B bude: F \u003d 30x 1 + 40x 2
Poďme nájsť riešenie problému pomocou jeho geometrickej interpretácie.
Za týmto účelom v nerovnostiach systému obmedzení prejdeme na rovnosť a zostrojíme zodpovedajúce priame čiary:
Nájdeme súradnice bodu B - priesečníky priamok:
Po vyriešení tohto systému rovníc dostaneme: x 1 \u003d 12; x 2 \u003d 18
Ak teda podnik vyrába 12 výrobkov typu A a 18 výrobkov typu B, získa maximálny zisk rovný
F max \u003d 30 12 + 40 18 \u003d 1080 rubľov.
Príklad 2.
Vyriešte LPP
max (min) F \u003d 2x 1 + 3x 2;
Rozhodnutie. Aby sme vytvorili oblasť realizovateľných riešení, zostrojíme v systéme x 1 Ox 2 hraničné čiary zodpovedajúce týmto obmedzeniam nerovnosti:
x 1 + x 2 ≤ 6, x 1 + 4x 2 ≥ 4, 2x 1 -x 2 ≥ 0.
Nájdite polroviny, v ktorých tieto nerovnosti držia. K tomu je vzhľadom na konvexnosť ktorejkoľvek polroviny postačujúce vziať ľubovoľný bod, ktorým príslušná hraničná čiara neprechádza, a skontrolovať, či tento skúšobný bod spĺňa obmedzenie nerovnosti. Ak áno, potom táto nerovnosť platí v polrovine obsahujúcej skúšobný bod. V opačnom prípade sa vezme polrovina, ktorá neobsahuje vzorkový bod. Ako testovací bod je často vhodné brať pôvod súradníc O (0; 0). Pre náš príklad je oblasťou realizovateľných riešení množina bodov štvoruholníka ABCD (obr. 6).
Zostrojíme vektor c \u003d (c 1; c 2) \u003d (2; 3). Pretože je potrebné iba objasniť smer zväčšenia objektívnej funkcie, niekedy je pre väčšiu prehľadnosť vhodné skonštruovať λс (λ\u003e 0). Nakreslite vodorovnú čiaru F \u003d 0 kolmo na vektor c. Paralelným pohybom priamky F \u003d 0 nájdeme krajný bod B., v ktorom objektívna funkcia prevezme maximálnu hodnotu, a bod A, v ktorom sa dosiahne minimálna hodnota.
Súradnice bodu B určuje systém
Odtiaľ Fmax \u003d F (A) \u003d 32/9
ÚLOHY NEZÁVISLÉHO RIEŠENIA
Riešenie úloh 1.1-1.10 graficky.
Problém s viacerými premennými
Zvážte nasledujúci problém lineárneho programovania
Aby sme to graficky vyriešili, je potrebné transformovať systém obmedzení tak, aby systém vo forme hlavného problému neobsahoval viac ako 2 premenné.
To je možné vykonať postupne, s výnimkou premenných alebo Jordan-Gaussovej metódy. Zvážte Jordan-Gaussovu metódu.
stôl 1
| x 1 | x 2 | x 3 | x 4 | x 5 | b | |
7 3 2 2 | 3 1 1 1 | 6 3 3 -1 | 1 1 0 0 | 1 0 1 -1 | 10 3 4 0 |
(-3) 1 , (-1) 3,4
tabuľka 2
| x 2 |
-2 3 1 -1 |
0 1 0 0 |
-3 3 0 -4 |
-2 1 1 -1 |
1 0 -1 -1 |
1 3 -1 -3 |
(2) 1 , (-1) 2 ,(1) 3
Tabuľka 3
x 2 x 4 |
0 2 1 0 |
0 1 0 0 |
3 3 0 -4 |
0 0 1 0 |
1 1 -1 -2 |
1 4 -1 -4 |
(-1) 2 , (1) 3 ,(2) 4
Tabuľka 4
|
x 5 x 2 x 4 |
0 2 1 0 |
0 1 0 0 |
3 0 3 2 |
0 0 1 0 |
1 0 0 0 |
1 3 0 -2 |
(-1) 2 , (1) 3 ,(2) 4
Nezávažné povolené neznáme nezbavíme negatívnych rovníc obmedzenia
x 2, x 4, x 5 a nahradíme znamienko rovnosti znakmi nerovnosti, dostaneme pomocný problém lineárneho programovania s dvoma premennými:
F (x) \u003d 2 x 3 +2 → max
F (x) \u003d 0: 2 x 3 +2-0 (0; -1); (5; -1)
F max \u003d 2 pri x 1 \u003d 0; x 3 \u003d 0
3. JEDNODUCHÁ METÓDA RIEŠENIA PROBLÉMU S LINEÁRNYM PROGRAMOVANÍM
3.1. Geometrická interpretácia simplexnej metódy
Ak je problém lineárneho programovania optimalizovaný, potom optimum zodpovedá rohovému bodu (najmenej jednému) O.D.R. a zhoduje sa s najmenej jedným z nezáporných základných riešení. Pri pohľade na konečné množstvo nezáporných základných riešení systému teda z nich vyberieme také, ktoré zodpovedá extrémnej hodnote objektívnej funkcie. Graficky to znamená, že iterujeme cez rohové body mnohostenného riešenia, čím sa zvyšuje hodnota objektívnej funkcie.
Simplex metóda pozostáva z:
1) stanovenie počiatočného prípustného základného riešenia problému;
2) prechod na lepšie riešenie;
3) kontrola optimálneho uskutočniteľného riešenia.
3.2. Tabuľková interpretácia simplexnej metódy
Na riešenie problémov lineárneho programovania napísaných v kanonickej podobe sa používa simplexná metóda:
Nájdite optimálne riešenie
X \u003d (x 1, x 2, ..., x n) (3,1)
uspokojenie systému obmedzení (rovníc)
Σa ij x j \u003d b i (i \u003d 1, m) (3,2)
j \u003d 1
a podmienky x j ≥ 0 (j \u003d 1, n)
a poskytnutie extrémnej hodnoty objektívnej funkcie
Z (x) \u003d Σ c j x j (3,3)
j \u003d 1
Nechajme nájsť počiatočné nezáporné základné riešenie systému (3.2), kde x 1, x 2, x 3… x m sú základné neznáme a x m + 1, x m + 2,…, x n sú neznáme neznáme.
Potom sa systém (3.2) zmení na povolený systém
(3.4)
Tento systém zodpovedá nezápornému základnému riešeniu formulára
X 0 \u003d (b 1, b 2, ..., b m, 0,0 ... 0)
Výsledné riešenie dosaďte do objektívnej funkcie
Δ 0 \u003d L (X 0) \u003d Σ C j B j (3,5)
J \u003d 1
a transformuj to tak, že to závisí iba od voľných neznámych x m + 1, x m + 2, ... x n
Vyjadrujeme všetky základné neznáme x 1, x 2, x 3 ... x m v zmysle zadarmo x m + 1, x m + 2, ... x na dosaďte ho do objektívnej funkcie.
Potom má objektívna funkcia tvar (3.6)
Zavádzame koncept odhadu Δ j voľných neznámych
(3.7)
Potom má objektívna funkcia formu
(3.8)
Uveďme vektory C \u003d (c 1, c 2, ..., c m) a B \u003d (a 1j, a 2j, ..., a mj) (j \u003d m + 1, n) , potom rovnosť (3.7) možno zapísať do vektorovej formy
Δ j \u003d CB j -c j (3,9)
Rovnosť (3.8) sa charakterom záznamu nelíši od rovníc systému, preto ho pridáme do tohto systému a získame rozšírený systém:
Výsledky vykonaných transformácií zaznamenané vo forme systému je možné zadať do tejto jednoduchej tabuľky:
| B.N. | C. | B | c 1 | c 2 | ... | c m | c m + 1 | ... | c j | ... | c n |
| x 1 | x 2 | ... | x m | x m + 1 | ... | x j | ... | x n | |||
| x 1 | c 1 | β 1 | 1 | 0 | ...
| 0 | a 1 (m + 1) | ...
| a 1j | ...
| 1n |
| x 2 | c 2 | β 2 | 0 | 1 | ...
| 0 | a 2 (m + 1) | ...
| a 2j | ...
| 2n |
| ... | ... | ... | ...
| ...
| ... | ...
| ...
| ...
| ...
| ...
| ...
|
| x m | c m | β m | 0 | 0 | ...
| 1 | a m (m + 1) | ...
| a mj | ...
| mn |
| L (X) | Δ j ≥0 | Δ 0 | 0 | 0 | ...
| 0 | Δ m + 1 | ...
| Δ j | ...
| Δ n |
prvý stĺpec obsahuje základné neznáme x 1, x 2, ..., x m; stĺpec C obsahuje koeficienty z objektívnej funkcie zodpovedajúce týmto základným neznámym; v stĺpci B - voľné pojmy rovníc systému zhodujúcich sa s kladnými zložkami pôvodného nezáporného základného riešenia X 0. Pod neznámymi x 1, x 2, ..., x n obsahujú stĺpce koeficienty zo systému.
Posledný riadok tejto tabuľky, ktorý sa nazýva skóre alebo index, s vypočítané podľa vzorcov. Pri prechode z jedného základného riešenia dodo inej, hodnotiacu linku je možné vypočítať aj podľa pravidla priamo gon (Jordan-Gaussova metóda).
V odhadovanej priamke nerovnosť Δ j ≥0 znamená kritérium optimality základného plánu.
Algoritmus riešenia LPP pomocou simplexnej metódy.
1. Nájdite referenčný plán.
2. Vytvorte simplexnú tabuľku.
3. Zistite, či existuje aspoň jedno záporné číslo Δ j
Ak nie, potom je nájdený referenčný plán optimálny. Ak medzi číslami je Δ j záporných, potom sa zistí buď nerozhodnuteľnosť problému. či, alebo prejsť na novú základnú čiaru.
4. Nájdite popredný stĺpec a riadok. Najväčší stĺpec je určený najväčším záporným číslom v absolútnej hodnote Δ j a vodiaci riadok je minimom pomerov zložiek stĺpca vektora Р 0 k kladným zložkám vodiaceho stĺpca.
5. Pomocou vzorcov (3.7) - (3.9) určite pozitívne zložkynový referenčný plán, koeficienty rozťažnosti vektorov Р j vo vektoroch nový základ a počet. Všetky tieto čísla sú napísané novým simplexomstôl.
6. Skontrolujte nájdený plán na optimálnosť. Ak plán nie je optimálny a je potrebné prejsť na nový základný plán, vráťte sa ku kroku 4 a v prípade získania optimálneho plánu alebo zostavenia plánu končí proces riešenia problému končí.
Príklad 3.1.
Na výrobu rôznych výrobkov A, B a C používa spoločnosť tri rôzne druhy surovín. Miera spotreby surovín na výrobu jedného výrobku každého druhu, cena jedného výrobku A, B a C, ako aj celkové množstvo suroviny každého druhu, ktoré sa dajú použiť na výrobumy, na sú uvedené v tabuľke.
Vypracovať výrobný plán výrobkov, v ktorom budú uvedené celkové náklady všetkých vyrobených výrobkov sa maximalizuje.
Rozhodnutie:
Vytvorme matematický model. Označujeme:
x 1 - výroba výrobkov typu A;
x 2 - výroba predmetov typu B;
х3 - výroba výrobkov typu C.
Zapíšme si systém obmedzení:
Celková hodnota vyrobeného tovaru je:
F \u003d 9x 1 + 10x 2 + 16x 3
Pokiaľ ide o ekonomický obsah, premenné x 1, x 2, x 3 môžu nadobúdať iba nezáporné hodnoty:
x 1, x 2, x 3 ≥0
Tento problém píšeme vo forme hlavného LPP, pre ktorý prechádzame zo systému nerovností na rovnosti, pre tento účel uvádzame ďalšie tri premenné:
Ekonomickým významom nových premenných je množstvo surovín jedného alebo druhého typu, ktoré sa nepoužívajú pre daný výrobný plán.
Napíšme transformovanú sústavu rovníc vo vektorovej podobe:
x 1 P 1 + x 2 P 2 + x 3 P 3 + x 4 P 4 + x 5 P 5 + x 6 P 6 \u003d P 0
kde
Pretože medzi vektormi Рj sú tri jednotkové vektory, potom je pre tento problém možné napísať referenčný plán X \u003d (0, 0, 0, 360, 192, 180) určený sústavou jednotkových vektorov Р 4, Р 5, Р 6, ktoré tvoria základ trojrozmerného priestoru.
Vypracujeme simplexnú tabuľku I iterácie a vypočítame hodnoty F 0, z j -c j.
Pôvodný plán kontrolujeme na optimálnosť:
Fo \u003d (C, P0) \u003d 0; z 1 \u003d (C, Pi) \u003d 0; z2 \u003d (C, P2) \u003d 0; z3 \u003d (C, P3) \u003d 0;
z 1-c 1 \u003d 0-9 \u003d -9; z2-c2 \u003d 0-10 \u003d -10; z 3-c3 \u003d 0-16 \u003d -16;
Pre bázové vektory z j -c j \u003d 0 (j \u003d 4,5,6).
Maximálne záporné číslo Δ j je v 4. riadku stĺpca P 3. Preto do základu zavedieme vektor Р 3. Definujme vektor, ktorému podliehame eliminácia z bázy, pre toto nájdeme Θ 0 \u003d min (b i / a ij) pre i3\u003e 0 t.j. Θ \u003d min. (360/12; 192/8; 180/3) \u003d 192/8 \u003d 24.
Tých. limitujúcim faktorom pre výrobu výrobkov C je dostupný objem surovín typu II. S prihliadnutím na jeho dostupnosť môže podnik vyrobiť 24 produktov C, zatiaľ čo surovina typu II bude úplne spotrebovanávano.
Preto musí byť vektor Р 5 vylúčený zo základne. Stĺpec vektory Р 3 a 2. rad sú vodiace čiary.
Zostavme tabuľku iterácie II. Najskôr vyplníme riadok vektora novo zadaného do základne, t.j. vodiaca čiara 2. Prvky tejto čiary sa získajú vydelením zodpovedajúcich prvkov tabuľky 1 povoľujúci prvok (t. j. 8). V tomto prípade do stĺpca C b napíšeme koeficientycient С 3 \u003d 16, stojaci v stĺpci vektora Р 3 zavedeného do základne
Na určenie zostávajúcich prvkov tabuľky II použijeme pravidlo trojuholníka.
Vypočítajme prvky tabuľky II v stĺpci P 0.
Prvý prvok - nájdite tri čísla
1) číslo stojace v bode 1 na križovatke stĺpca P0 a 1. riadku (360);
2) číslo stojace v bode 1 na križovatke stĺpca P3 a 1. riadku (12);
3) číslo stojace v bode 2 na križovatke stĺpca P0 a druhého radu (24).
360-12 24 \u003d 72
Druhý prvok bol vypočítaný skôr (Θ 0 \u003d 192/8 \u003d 24)
Tretím prvkom je
1) číslo stojace v bode 1 na križovatke stĺpca P0 a 3. riadku (180);
2) počet stojaci v bode 1 na križovatke stĺpca P3 a 3. riadku (3);
3) číslo stojace v bode 2 na križovatke stĺpca P0 a druhého radu (24).
180-324 \u003d 108
Hodnota F 0 v 4. riadku toho istého stĺpca sa dá nájsť dvoma spôsobmibami:
1) vzorcom Fo \u003d (C, P0) \u003d 0 72 + 16 24 + 0 108 \u003d 384;
2) podľa pravidla trojuholníka:
Vypočítajme prvky vektora Р 1 v.2. Vezmeme prvé dve čísla zo stĺpatsov R1 a R3 obj. 1,
a tretie číslo je z bodu 2 na križovatke 2. riadku a stĺpca Р1.
18-12 (3/ 4) = 9; 5-3 (3/ 4)=11/ 4.
Číslo z 1 -c 1 v 4. riadku stĺpca vektora P 1 v tabuľke 2
možno nájsť dvoma spôsobmi:
1) vzorcom z 1 -с 1 \u003d (C, P 1) -c 1 máme:
0 9 + 16 3/4 + 0 11 / 4-9 \u003d 3
2) podľa pravidla trojuholníka dostaneme:
-9-(-16) 3/ 4 = 3
Podobne nájdeme prvky stĺpca vektora P 2.
Prvky stĺpca vektora Р 5 sa počítajú podľa pravidla trojuholníka.
vyzerajú inak; trojuholníky však zostrojili tak, aby definovali tieto prvky
Pri výpočte prvku 1. riadku zadaného stĺpca dostanemetrojuholník tvorený číslami 0; 12 a 1/8. Preto hľadaliprvok je rovnaký
0 – 12 (1/8) = -3/2.
Položka v 3. riadku tohto stĺpca je
0 - 3 (1 /8) = -3/8.
Na konci výpočtu všetkých prvkov bola v tabuľke II uvedená novázákladný plán a koeficienty rozťažnosti vektorov Р j z hľadiska záklvektory P4, P3, P6 a hodnoty F0 "Δj".
Ako vidíte z tejto tabuľky, nová základná čiara problému jeplán X \u003d (0; 0; 24; 72; 0; 108).
Problémový plán nájdený v iterácii II nie je optimálny.
tento riadok má záporné číslo - 2. Je to zrejmé aj zo 4. riadku tabuľky 2, pretože v stĺpci vektora P 2 .
To znamená, že vektor P 2 by mal byť zavedený do základne, to znamená, že nový plán by mal počítať s uvoľnením V.
Pri určovaní možného počtu výroby výrobkov B by sa malo brať do úvahy dostupné množstvo surovín každého druhu, a to: výstup výrobkov B je určený min (bi "/ ai 2") pre i2 "\u003e 0, t. j. nájdeme Θ 0 \u003d min (72/9; 24 · 2/1; 108 · 2/3) \u003d 72/9 \u003d 8.
Preto je vektor P4 vylúčený zo základu, inými slovami, produkcia produktov B je obmedzená surovinami typu I, ktoré má podnik k dispozícii. Ak vezmeme do úvahy dostupné objemy tejto suroviny, mal by podnik vyrobiť 8 produktov B. Číslo 9 je rozlišovacím prvkom a stĺpec vektora P2 a prvý riadok tabuľky 2 sú vodítkami.
Zostavme tabuľku pre iteráciu III.
V tabuľke III najskôr vyplníme prvky 1. riadku, ktorým je riadok vektora P2 novo zavedeného do základu. Prvky tohto riadku sa získajú z prvkov prvého radu tabuľky 2 vydelením posledného prvku rozlišovacím prvkom (t. J. 9).
V tomto prípade do stĺpca C b tohto riadku zapíšeme s 2 \u003d 10.
Potom vyplníme prvky stĺpcov vektorov základne a podľa pravidla trojuholníka vypočítame prvky zvyšných stĺpcov.
Výsledkom je, že v tabuľke III získame nový referenčný návrh X \u003d (0; 8; 20; 0; 0; 96) a koeficienty rozťažnosti vektorov Pj prostredníctvom základných vektorov P 1, P 2 a P 3 zodpovedajúce hodnoty F 0 "" a Δ j ...
Skontrolujeme, či je daný základný plán optimálny alebo nie. Zvážte štvrtý riadok, tabuľku 3. Tento riadok neobsahuje žiadne záporné čísla. To znamená, že nájdený základný plán je optimálny a Fmax \u003d 400.
Preto je výrobný plán, ktorý zahŕňa výrobu 8 výrobkov B a 20 výrobkov C, optimálny. V rámci tohto výrobného plánu sú suroviny typu I a II plne využité a 96 kg surovín typu III zostáva nevyužitých a náklady na vyrobené výrobky sú 400 EUR.
Optimálny výrobný plán nezabezpečuje výrobu výrobkov A. Zavedenie výrobkov typu A do výrobného plánu by viedlo k zníženiu uvedených celkových nákladov. Vidno to zo 4. riadku stĺpca vektora P1, kde číslo 5 ukazuje, že pri danom pláne vedie zahrnutie uvoľnenia jednotky produktu A do neho iba k zníženiu celkovej hodnoty nákladov o 5 €.
Príklad 3.2
Vyplňte úvodnú simplexnú tabuľku pre nasledujúci LPP:
Rozhodnutie:
Urobme nasledovné v uvedenom poradí:
-na druhý riadok napíšeme neznáme x 1, x 2, ..., x 5;
-v prvom riadku nad nimi - zodpovedajúce koeficienty 3, -2, 1,4, -1 od objektívnej funkcie;
- pod neznámami x 1, x 2, ..., x 5, vyplňte stĺpce tvorené zodpovedajúcimi koeficientmi na ľavej strane rovníc pôvodného systému;
-v stĺpci zapíšeme voľné výrazy rovníc 3,1,5;
-v prvom stĺpci B. p. dať neznámy x 2 , X 3 , X 5 , keďže sa pod nimi nachádzajú jednotkové stĺpce, a preto ich budeme považovať za základné; základné neznáme sú usporiadané v takom poradí, aby jednotky v stĺpcoch boli na križovatke identických neznámych;
- do stĺpca zapíšeme koeficienty -2,1, -1, z objektívnej funkcie s vybranými základnými neznámymi x 2 , X 3 , X 5 ;
-vyplňte odhadovaný riadok takto: do stĺpca B vložte číslo Δ 0 vypočítané podľa vzorca (3.5); pod základnými neznámymi x 2 , X 3 , X 5 - nuly, ktoré možno získať aj z rovnosti (3.9); pod voľnými premennými x 1 , X 4 - zapíšeme si hodnoty získané z rovnosti (3.9).
Výsledky týchto akcií zapíšeme do nasledujúcej tabuľky:
Vyberme si ako rozlišovací stĺpec x 4, ako najviac „zlý“ (zodpovedá najväčšiemu negatívnemu odhadu v absolútnej hodnote). Ďalej si predstavíme riadiaci riadok nasledovne: pre kladné koeficienty stĺpca x 4 vypočítame pomery b i / a i4 a zapíšeme ich do grafu θ.
Najmenšie číslo určí rozlišujúci reťazec. Nepovažujeme záporné a nulové koeficienty z dôvodu nezápornosti pravej strany rovníc systému a požiadavky aspoň na nezníženie objektívnej funkcie.
Na priesečníku rozlišovacej čiary a stĺpca riešenia vyberte prvok riešenia. Urobme rozlišovací prvok rovným jednému, pre ktorý vydelíme celý prvý riadok dvoma. Ďalej transformujeme tabuľku pomocou metódy Jordan-Gauss.
Kritérium optimality je teda splnené už v tabuľke druhého kroku. Dostali sme optimálny plán X (0; 0; 11/2; 3/2; 13/2), max L (X) \u003d 5.
ÚLOHA 1. Simplexná metóda riešenia problémov lineárneho programovania
Na výrobu rôznych druhov výrobkov 1, 2, 3 a 4 podnik používa tri druhy surovín A, B a C. Miera spotreby surovín na výrobu jednotky každého druhu výrobku, cena jedného výrobku a zásoby každého druhu zdrojov sú známe a sú uvedené v tabuľke 1.1.
Vypracovať plán výroby výrobkov, v ktorom spoločnosť získa maximálny zisk.
Podľa možnosti vyberte počiatočné údaje o probléme v tabuľkách 1.1, 1.2.
Tabuľka 1.1 - Pomery nákladov na zdroje na jednotku produktu každého typu (spoločné pre všetky možnosti)
| ZDROJ | TYPY VÝROBKOV | Skladom | |||
| 1 | 2 | 3 | 4 | ||
| A | 6 | 8 | 4 | 7 | a 5 |
| IN | 0,75 | 0,64 | 0,5 | 0,8 | a 6 |
| ZO | 8 | 12 | 10 | 14 | a 7 |
| EKONOMICKÉ | a 3 | a 4 | MAX | ||
Plán riešenia problému:
- vyberte zdrojové údaje svojej verzie z tabuliek;
- určiť neznáme úlohy;
- tvoria systém obmedzení a cieľovej funkcie úlohy;
- uviesť systém obmedzení do kanonickej podoby určením a zavedením ďalších premenných;
- nakreslite simplexnú tabuľku a naplňte ju pôvodným základným plánom;
- pomocou algoritmu simplexovej metódy nájdite optimálne riešenie problému;
PROBLÉM 2
Riešenie problému otvorenej dopravy potenciálnou metódou
Veľkoobchodné sklady A 1, A 2, A 3, A 4 majú zásoby určitého produktu v známych množstvách, ktoré je potrebné doručiť do obchodov B 1, B 2, B 3, B 4, B 5. Známe sú aj tarify za prepravu jednotky produktu z z každého skladu do každého obchodu.
Nájdite možnosť pripojenia obchodov k skladom, v ktorých by bola výška nákladov na prepravu minimálna.
V súlade s možnosťou vyberte počiatočné údaje o probléme v tabuľkách 2.1, 2.2.
Tabuľka 2.1 - Matica taríf (spoločná pre všetky možnosti)
| Veľkoobchodné sklady | Obchody | Zásoby | ||||
| V 1 | V 2 | O 3 | AT 4 | O 5 | ||
| A 1 | 5 | 4 | 10 | 7 | 8 | a 6 |
| A 2 | 7 | 6 | 7 | 10 | 6 | a 7 |
| A 3 | 2 | 9 | 5 | 3 | 4 | a 8 |
| A 4 | 6 | 11 | 4 | 12 | 5 | a 9 |
| Potreby | a 3 | a 4 | ||||
Plán riešenia problému:
- Skontrolujte, či je vyriešený problém zatvorený alebo otvorený.
- Ak je problém otvorený, vykonajte činnosti, ktoré ho umožnia začať riešiť.
- Nakreslite maticu problému s dopravou a zapíšte si do nej základný plán pomocou jednej z metód známeho základného plánu (metóda severozápadného rohu, najlepšia tarifa, dvojitá preferencia).
- Skontrolujte zostavený plán podpory, či nedôjde k degenerácii. V prípade potreby vykonajte opatrenia na prekonanie zdegenerácie plánu podpory.
- Vypočítajte hodnotu objektívnej funkcie pre základný plán.
- Vypočítajte potenciály riadkov a stĺpcov pomocou pravidiel metódy potenciálu.
- Pomocou nájdených potenciálov skontrolujte optimálnosť vytvoreného plánu podpory.
- Ak je riešenie optimálne, choďte na krok 13.
- Ak riešenie nie je optimálne, je potrebné ho vylepšiť. Aby ste to dosiahli, musíte nájsť bunku matice dopravného problému, ktorý sa má vylepšiť, vytvoriť pre ňu uzavretý cyklus a určiť množstvo zdrojov, ktoré sa majú pohybovať po vrcholoch tohto cyklu.
- Presúvajte zdroje pozdĺž vrcholov cyklu bez narušenia rovnováhy medzi riadkami a stĺpcami matice.
- Prejdite na krok 6.
- Vypíšte optimálne riešenie a vykonajte jeho ekonomickú analýzu.
ÚLOHA 3. Optimálne rozdelenie zdrojov.
Predstavenstvo spoločnosti zvažuje návrh na zvýšenie výrobnej kapacity na zvýšenie produkcie homogénnych výrobkov v štyroch podnikoch vlastnených spoločnosťou.
Na modernizáciu podnikov správna rada investuje 250 miliónov rubľov. s diskrétnosťou 50 miliónov rubľov. Prírastok produkcie závisí od alokovaného množstva, jeho hodnoty poskytujú podniky a sú uvedené v tabuľke.
Nájdite ponuku investícií medzi podnikmi, ktorá firme zabezpečí maximálny nárast produkcie, a na jeden podnik je možné investovať iba jednu investíciu.
Podľa možnosti vyberte počiatočné údaje o probléme v tabuľkách 3.1, 3.2.
Tabuľka 3.1 - Hodnoty parametrov úlohy
| Investície, milión rubľov | Zvýšenie výrobnej produkcie, milión rubľov | |||
| Spoločnosť | Spoločnosť | Spoločnosť | Spoločnosť | |
| 50 | a 11 | a 12 | a 13 | a 14 |
| 100 | a 21 | a 22 | a 23 | a 24 |
| 150 | a 31 | a 32 | a 33 | a 34 |
| 200 | a 41 | a 42 | a 43 | a 44 |
| 250 | a 51 | a 52 | a 53 | a 54 |
Plán riešenia problému:
- V tabuľkách vyberte zdrojové údaje svojej verzie.
- Rozdeľte riešenie problému na etapy podľa počtu podnikov, do ktorých sa má investovať.
- Vytvorte vzťahy opakovania
- Vykonajte prvú fázu výpočtu, keď sú investície alokované iba do prvého podniku
- Vykonajte druhú fázu výpočtu, keď sú investície pridelené prvému a druhému podniku
- Vykonajte tretiu etapu výpočtu, keď sú investície pridelené 1-3 podnikom
- Vykonajte štvrtú etapu výpočtu, keď sa investície rozdelia medzi štyri podniky
- Vypíšte optimálne riešenie a vykonajte jeho ekonomickú analýzu.

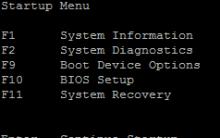





Farebný profil - zadarmo
Prečo nič nefunguje, keď otvorím Photoshop
Ako odstrániť šum z fotografie Program na odstránenie šumu zo zvukového záznamu
Kovové textúry, škrabance
Základy imidžu