Дешифраторы и шифраторы. Задание к работе

Статистическое исследование нелинейных систем представляет собой весьма сложную задачу. Сравнительная простота методов статистического анализа линейных систем является естественной причиной попыток распространить эти методы на задачи приближенного исследования точности нелинейных систем. Так возникли методы линеаризации нелинейных характеристик систем.

Простейшим видом линеаризации нелинейных систем является линеаризация при помощи разложения всех нелинейных функций, входящих в уравнения системы, в ряд Тейлора и отбрасывание всех членов ряда выше первой степени. При этом каждая входящая в уравнение системы нелинейная функция заменяется приближенным линейным выражением

где - математическое ожидание случайной функции х.

Формула вида (XVII.1) позволяет лйнеаризовать уравнения нелинейной системы относительно флюктуаций сигналов в различных элементах системы. Это дает возможность применять для приближенного исследования точности нелинейных систем методы статистической теории линейных систем. Однако формулы вида (XVII. 1) применимы только к непрерывным функциям, имеющим непрерывные производные по аргументу в области его практически возможных значений.

Между тем системы автоматического регулирования часто содержат существенно нелинейные звенья, характеристики которых разрывны или имеют разрывные производные. К таким характеристикам можно отнести релейные характеристики, ограниченные зоны линейности и т. д. (см. кн. 1 гл. IV). Для линеаризации таких характеристик был развит метод статистической линеаризации , .

Статистическая линеаризация представляет собой замену нелинейного звена линейным относительно флюктуаций звеном с сохранением в определенном смысле уровня полезного сигнала и уровня флюктуаций на выходе. При этом нелинейная функция аппроксимируется постоянным эквивалентным линейным коэффициентом усиления. Естественно, что аппроксимация нелинейных функций постоянным коэффициентом недостаточно полно

отражает физическую картину преобразования случайного сигнала, так как не учитывается преобразование спектра сигнала нелинейным звеном. В связи с этим в работе была предложена аппроксимация безынерционных нелинейных звеньев статистически эквивалентной передаточной функцией, определяемой из отношения спектральной плотности сигнала на выходе нелинейного звена к спектральной плотности сигнала на входе.

Одновременно с этим была развита статистическая линеаризация нелинейных функций при условии, когда входной сигнал содержит периодическую составляющую. Этот метод в дальнейшем получил название совместной статистической и гармонической линеаризации.

Названные методы линеаризации позволяют свести систему нелинейных дифференциальных уравнений к системе линейных, эквивалентных исходной по первым двум моментам случайной функции. Следовательно, используя метод статистической линеаризации, можно определить лишь среднее значение и дисперсию случайной функции. При использовании совместной линеаризации можно определить так же первую гармонику периодических колебаний в нелинейной системе.

В связи с тем, что в нелинейной системе функция плотности вероятности случайного сигнала может существенным образом отличаться от нормальной и при этом для характеристики точности работы знание лишь первых двух моментов не является достаточным в работе 113], был развит метод обобщенной статистически эквивалентной передаточной функции, основанный на разложении в ряд по ортогональным полиномам Чебышева - Эрмита случайных функций и позволяющий определить высшие моменты этих функций в нелинейной системе.

Основная идея метода статистической линеаризации , заключается в аппроксимации существенно нелинейных преобразований линеаризованной зависимостью, эквивалентной нелинейному преобразованию по первым двум моментам случайных функций, т. е. по среднему значению и дисперсии. Разумеется, что эта эквивалентная линеаризованная зависимость имеет различный вид для разных существенно нелинейных элементов, а также зависит от вероятностных характеристик случайного сигнала на входе нелинейного элемента.

Рассмотрим нелинейное преобразование, соответствующее реальной статической характеристике безынерционного нелинейного элемента

Преобразуемый случайный процесс может быть представлен в виде

где математическое ожидание, а процесс с нулевым математическим ожиданием.

Представим сигнал на выходе нелинейного элемента в виде эквивалентного линейного преобразования входного сигнала

где К - эквивалентные статистические передаточные коэффициенты по математическому ожиданию и дисперсии, которые необходимо определить. Первое предположение, являющееся исходным при определении этих коэффициентов, - это соблюдение равенств математического ожидания и дисперсии для случайного сигнала на выходе реального нелинейного и эквивалентного линейного элементов. Тогда коэффициент может быть определен как отношение математического ожидания на выходе нелинейного элемента к математическому ожиданию сигнала на входе

Для коэффициента в этом случае будем иметь выражение

где - средние квадратические отклонения центрированных случайных сигналов соответственно на входе и на выходе нелинейного элемента.

Второе предположение, принимаемое при статистической линеаризации, основано на требовании минимума среднего квадрата разности между случайным сигналом на выходе нелинейного элемента и случайным сигналом на выходе эквивалентного линейного элемента. Это условие можно записать следующим образом:

Раскроем это выражение:

В формуле (XVI 1.8) черта сверху означает математическое ожидание. Взяв частные производные от выражения (XVI 1.8) по получим

где - взаимная корреляционная функция сигналов на входе и на выходе эквивалентного линейного элемента при

Использование при расчетах коэффициента (XVI 1.6) дает несколько завышенное значение дисперсии, а использование коэффициента (XVI 1.9) несколько заниженное. Поэтому при расчетах в качестве эквивалентного коэффициента по случайной составляющей можно взять следующее значение:

Заметим, что при статистической линеаризации в отличие от обычной линеаризации нелинейных функций, основанной на их разложении в ряд Тейлора в окрестности некоторой рабочей точки, средние характеристики сигналов могут быть рассчитаны точно.

Теперь рассмотрим общие формулы для определения эквивалентных коэффициентов усиления. Пусть задана одномерная нормальная плотность вероятности). Тогда формулы для коэффициентов будут иметь вид

Произведем расчет коэффициентов по формулам (XVII. 11), (XVII.12) и (XVII.13) для нелинейной характеристики типа кубической параболы, которая аналитически может быть представлена формулой

Метод гармонической линеаризации позволяет с достаточной для практики точностью исследовать устойчивость и точность нелинейных систем, используя методы, разработанные для линейных систем. Метод дает возможность определить наличие автоколебаний, а также их частоту и амплитуду.

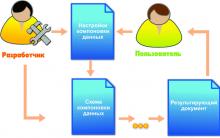
Нелинейная система представляется в виде соединения линейной и нелинейной части (рис. 5).

Рис. 5 Схема нелинейной системы

Выходной сигнал нелинейной части системы в общем случае определяется выражением

Обозначим как передаточную функцию линейной части. Система уравнений примет вид

Найдем условия, при которых на выходе линейной части системы возникают гармонические колебания вида

В этом случае сигнал y(t) нелинейной части будет представлять собой также периодическую функцию, но отличную от синусоиды. Эту функцию можно разложить в ряд Фурье

В этом выражении a i и b i - коэффициенты Фурье. Для симметричных нелинейностей F 0 =0.

Основным условием, которое накладывает метод на линейную часть системы, является условие фильтра нижних частот. Считается, что линейная часть пропускает только первую гармонику колебаний. Данное допущение позволяет считать высшие гармоники в (7.19) несущественными и ограничиться рассмотрением только первой гармоники сигнала y(t).

то выражение (7.20) можно переписать в виде

Первое уравнение системы (7.17) примет вид

В этом выражении

Результат замены нелинейности F(x,sx) выражением

и называется гармонической линеаризацией. Величины q и q 1 называются коэффициентами гармонической линеаризации или просто гармоническими коэффициентами. Для однозначных нелинейностей обычно q 1 =0 . Формулы для гармонических коэффициентов, соответствующих типовым нелинейностям, приводятся в приложениях.

Принципиальное отличие гармонической линеаризации от обычной состоит в том, что при обычной линеаризации нелинейную характеристику заменяют прямой линией с определенной постоянной крутизной, а при гармонической линеаризации - прямой линией, крутизна которой зависит от амплитуды входного сигнала нелинейного элемента.

Рассмотрим методику определения амплитуды и частоты автоколебаний.

1). В характеристическом уравнении системы, полученном из (7.22) делаем замену s=j и получим

2). Из полученного выражения выделяем вещественную и мнимую части и приравниваем их нулю, что, по критерию Михайлова, соответствует нахождению системы на колебательной границе устойчивости.

• 3).Решение этой системы дает частоту и значения гармонических коэффициентов. Если эти значения вещественны и положительны, то в системе существует предельный цикл. По значениям гармонических коэффициентов можно определить амплитуду предельного цикла.
• 4). Общим признаком устойчивости предельного цикла, т.е. существования автоколебаний, является равенство нулю предпоследнего определителя Гурвица при полученных значениях амплитуды и частоты предельного цикла. Часто более удобно использовать условие устойчивости предельного цикла, в основе которого лежит критерий устойчивости Михайлова.

Если это неравенство выполняется, то предельный цикл устойчив и в системе существуют автоколебания с определенными выше амплитудой и частотой. Индекс ”*” означает, что производные вычислены при уже известных значениях гармонических коэффициентах, амплитуды и частоты.

Пример. Допустим, что в уже рассмотренной выше системе стабилизации угла тангажа самолета рулевой привод нелинейный и его структурная схема имеет вид, показанный на рис. 7.6.

Рис.6 Схема нелинейного рулевого привода

Зададим следующие параметры нелинейности скоростной характеристикм рулевого привода: b = 0.12, k 1 = tg =c/b = 6.7. Коэффициенты гармонической линеаризации этой нелинейности определяются выражениями

Заменив в схеме нелинейную характеристику гармоническим коэффициентом, получим передаточную функцию рулевого привода

Подставим эту передаточную функцию в структурную схему системы стабилизации угла тангажа и определим передаточную функцию замкнутой системы

В характеристическом уравнении замкнутой системы сделаем замену s = j и выделим вещественную и мнимую части.

Из второго уравнения системы получим выражение для частоты: , и подставив его в первое уравнение, после преобразований получим

Подставив сюда ранее определенные выражения для коэффициентов характеристического уравнения, можно получить квадратное уравнение относительно гармонического коэффициента, решив которое, найдем

По этим значениям можно вычислить для двух случаев все коэффициенты характеристического уравнения и определить частоты, соответствующие каждому значению q(А). Получим:

Оба значения гармонического коэффициента и соответствующие частоты вещественны и положительны. Следовательно, в системе существуют два предельных цикла. Значения амплитуды предельного цикла определяются численно путем подбора такого значения при котором формула для коэффициента гармонической линеаризации дает значение, равное ранее вычисленному. В рассматриваемом случае получим

Теперь оценим устойчивость предельных циклов. Используем неравенство, полученное из критерия Михайлова, для чего определим

Производная от коэффициента гармонической линеаризации, входящая в полученные выражения, вычисляется по формуле

Расчеты по выше приведенным формулам показывают, что первый предельный цикл не устойчив и возникает он при (0) 0.1166(6.7 0 ). Если начальное отклонение меньше указанного, то процесс на входе нелинейного элемента затухает (рис.7. 7) и система устойчива.

Если начальное значение угла тангажа больше указанного, то процессы сходятся ко второму предельному циклу, который устойчив и, таким образом в системе возникают автоколебания (рис. 8).

Рис. 8

Путем моделирования определено, что область притяжения устойчивого предельного цикла лежит приблизительно в пределах (0) 0.1167 - 1.4 (6.71 0 - 80.2 0 ).

Метод линеаризации операторов с точки зрения изложенной в предыдущих главах общей теории случайных функций может быть применен в двух различных вариантах. Во-первых, можно непосредственно линеаризовать заданную зависимость между случайными функциями и заменить таким образом нелинейные уравнения, связывающие случайные функции, линейными. Во-вторых, можно применить метод канонических разложений, который приводит к замене операций над случайными функциями операциями над обычными случайными величинами, после чего можно применить обычный в теории вероятностей метод линеаризации функциональных зависимостей между случайными величинами.

Метод непосредственной линеаризации преобразования случайных функций состоит в замене всех заданных уравнений, связывающих случайные функции, приближенными линейными уравнениями, достаточно хорошо отражающими истинную зависимость между случайными функциями в области практически возможных реализаций случайных функций. Так как математические ожидания случайных величин

являются средними значениями, около которых рассеиваются их возможные реализации, то практически удобнее всего производить линеаризацию соотношений между случайными функциями относительно их отклонений от математических ожиданий, т. е. центрированных случайных функций. При этом все функции, входящие в заданные уравнения, следует разложить в ряды Тейлора по центрированным случайным функциям и отбросить члены этих рядов выше первой степени. Степень точности получаемого таким образом приближения может быть оценка по максимальной возможной величине отброшенных членов в области практически возможных реализаций случайных функций. Заменив данные уравнения, связывающие случайные функции, приближенными линейными уравнениями, мы можем применить изложенную в предыдущей главе теорию линейных преобразований случайных функций для приближенного определения математических ожиданий и корреляционных функций случайных функций, полученных в результате рассматриваемого нелинейного преобразования. В следующем параграфе мы дадим более подробное изложение метода непосредственной линеаризации в применении к случайным функциям скалярной независимой переменной, связанным обыкновенными дифференциальными уравнениями.

Перейдем к применению метода канонических разложений к приближенному исследованию нелинейных преобразований случайных функций. Предположим, что случайная функция получается в результате преобразования случайной функции при помощи некоторого нелинейного оператора А:

Подставляя сюда вместо случайной функции какое-либо ее каноническое разложение, получим:

Это равенство представляет случайную функцию как некоторую, вообще говоря нелинейную, функцию случайных величин в которую аргумент 5 входит как параметр:

Линеаризуя эту функцию обычным в теории вероятностей способом (см. § 31) и принимая во внимтние, что математические ожидания величин равны нулю, будем иметь:

есть значение производной функции по случайной величине при нулевых значениях всех величин что и отмечено нуликом внизу у квадратной скобки. Формула (100.5) дает приближенное каноническое разложение случайной функции с коэффициентами разложения и координатными функциями

Принимая во внимание, что математические ожидания всех величин равны нулю, получим из (100.5) следующую приближенную формулу для математического ожидания случайной функции

Таким образом, для приближенного определения математического ожидания случайной функции следует в соотношении (100.1), связывающем случайные функции и заменить эти случайные функции их математическими ожиданиями Это правило вполне аналогично правилу приближенного определения математического ожидания случайной величины, связанной с другой случайной величиной нелинейной функциональной зависимостью, выведенному в § 31.

Корреляционная функция случайной функции на основании общей формулы (56.2), выразится приближенной формулой